一袋中有四只球，编号为1,2,3,4，从袋中一次取出两只球，用x表示取出的两只球的最大号码数，则A.0.4 B.0.5 C.0.6 D.0.7

题目
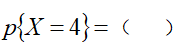
一袋中有四只球，编号为1,2,3,4，从袋中一次取出两只球，用x表示取出的两只球的最大号码数，则

A.0.4
B.0.5
C.0.6
D.0.7
相似考题

1.一个盒子中有4个球,球上分别标有号码0,1,1,2,从盒子中有放回的任意取出2个球,设X为取出的球上的号码的乘积,(1)求X的分布列;(2)P(X

2.：一个袋中有若干个红色和蓝色小球，如果从袋中取出一个红球，那么袋中剩下小球的1/7是红色的。把这个小球放回去，另取出2个蓝球，那么剩下球的1/5为红色球。袋中原来有多少个小球?（ ）A．15B．22C．30D．50

3.一个袋子中有5只黑球3只白球,从袋中任取两只球,若以A表示:“取到的两只球均为白球”;B表示:“取到的两只球同色”。则P(A)=();P(B)=()。

4.一袋中有5个乒乓球,编号分别为1,2,3,4,5从中任意去取3个,以X表示球中的最大号码,X=3的概率为:()A、0.1B、0.4C、0.3D、0.6

参考答案和解析
答案：B
解析：
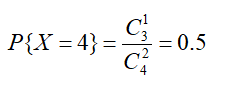
更多“一袋中有四只球，编号为1,2,3,4，从袋中一次取出两只球，用x表示取出的两只球的最大号码数，则”相关问题

  • 第1题：

    一个袋中有若干个红色和蓝色小球，如果从袋中取出一个红球，那么袋中剩下小球的1/7是红色的。把这个小球放回去，另取出2个蓝色的球。那么剩下球的1/5为红色球。袋中原来有多少个小球?（ ）

    A．15

    B．22

    C．30

    D．50


    正确答案：B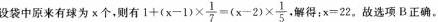

  • 第2题：

    一个口袋中装有3个一样的球，3个球上分别写有数字2，3和4。若第一次从袋子中取出一个球，记下球上的数字A，并将球放回袋中。第二次又从袋子中取出一个球，记下球上 的数字B。然后算出它们的积。则所有不同取j求情况所得到的积的和是（ ）。


    正确答案：D
    取球的情况有九种，它们的积之和为2×2+2×3+2×4+3×2+3×3+3×4+4×2+4×3+4×4=(2斗3+4)2=81。

  • 第3题：

    袋中有5个大小相同的球，其中3个是白球，2个是红球，一次随机地取出3个球，其中恰有2个是白球的概率是：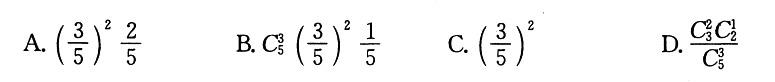


    答案：D
    解析：

  • 第4题：

    一个袋子中有5个球，编号为1，2，3，4，5，同时从中任取3个，以X表示取出的3个球中的最大号码，求随机变量X的概率分布.


    答案：
    解析：
    依题意，随机变量X只能取值3，4，5；且p｛X=

  • 第5题：

    袋子中有若干黑球和白球。若取出一个黑球，则袋中黑球占总球数的 2/7；若取出两个白球，则袋中白球占 2/3。从原来袋中抽出3个球，其中有且仅有1个黑球的概率：

    A.低于20%
    B.在20%—40%之间
    C.在40%—60%之间
    D.高于60%

    答案：C
    解析：
    第一步，本题考查概率问题，用方程法解题。

  • 第6题：

    设袋中有5个球,其中3个新球,2个旧球,从中任取3个球,用X表示3个球中的新球个数,求X的分布律与分布函数.


    答案：
    解析：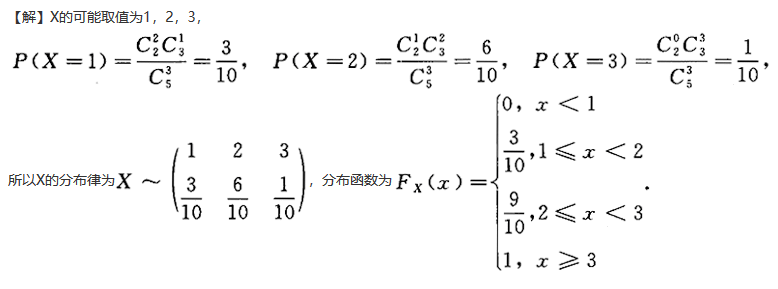

  • 第7题：

    袋中有1个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球.以X，Y，Z分别表示两次取球所取得的红球、黑球与白球的个数.
    (Ⅰ)求P{X=1｜Z=0}；
    (Ⅱ)求二维随机变量(X，Y)的概率分布.


    答案：
    解析：

  • 第8题：

    袋中有l个红色球，2个黑色球与三个白球，现有放回地从袋中取两次，每次取一球，以 X，Y，Z分别表示丽次取球所取得的红球、黑球与白球的个数。
    (1)求P{X=1|Z=0}；
    (2)求二维随机变量(X，Y)的概率分布。


    答案：
    解析：

  • 第9题：

    有5个编号为1、2、3、4、5的红球和5个编号为1、2、3、4、5的黑球，从这10个球中取出4个，则取出的球的编号互不相同的概率为（ ）.


    答案：D
    解析：

  • 第10题：

    一袋中有2个黑球和若干个白球，现有放回地摸球4次，若至少摸到一个白球的概率是80/81，则袋中白球的个数是（）。


    正确答案:4

  • 第11题：

    单选题
    一个盒子里有20个球，其中有18个红球，2个黑球，每个球除颜色外都相同，从中任意取出3个球，则下列结论中，正确的是(　　)
    A

    所取出的3个球中，至少有一个是黑球 

    B

    所取出的3个球中，至少有2个黑球

    C

    所取出的3个球中，至少有1个是红球  

    D

    所取出的3个球中，至少有2个是红球


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    袋子里红、黄、蓝、白四种颜色的球分别有3、4、5、6只，每次只能取出一只球，取出的球不再放回袋子，则至少要取多少次才能保证取出两只红球？（）
    A

    12

    B

    15

    C

    16

    D

    17


    正确答案： C
    解析： 考虑最差情况，先取出白、蓝、黄三种颜色的球，最后取出两个红色的球，要取6+5+4+2=17次。

  • 第13题：

    一个口袋中装有3个一样的球，3个球上分别写有数字2，3和4。若第一次从袋子中取出一个球，记下球上的数字A，并将球放回袋中。第二次又从袋子中取出一个球，记下球上的数字B，然后算出它们的积。则所有不同取球情况所得到的积的和是。

    A．52

    B．56

    C．75

    D．81


    正确答案：D

    取球的情况有九种，它们的积之和为

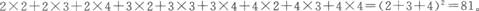
  • 第14题：

    袋中有几个球，取球规则是“每次取出袋中的一半后再放进一个”，算取一次，取了 832次后，袋中剩2个，则原袋中有( )个。

    A．2

    B．18

    C．4

    D．6


    正确答案：A
    12．  A  [本题考点] 该题是一种特例。
        [解题思路] 如果按部就班的计算，很难做出答案，而且浪费了时间，可以从另一个方面考虑：每次取的球数均是袋中球数的一半，所以取之前袋中的球肯定为偶数，该数的一半也必为奇数，满足这些条件的，只能是2，而不能是其他任何数。
       

  • 第15题：

    盒子里有同样数目的黑球和白球。每次取出8个黑球和5个白球，取出几次后，黑球没有了，白球还剩12个。则共取了（）。

    A.3次
    B.4次
    C.5次
    D.6次

    答案：B
    解析：
    共取了12÷（8－5）＝4次。故本题选B。

  • 第16题：

    一位乒乓球学员手中拿着装有7只乒乓球的不透明口袋,其中3只黄球，4只白球。他随机取出一只乒乓球，观察颜色后放回袋中，同时放入2只与取出的球同色的球，这样连续取2次，则他取出的两只球中第1次取出的是白球，第2次取出的是黄球的概率是

    A.8/77
    B.4/21
    C.2/11
    D.4/7

    答案：B
    解析：
    第一步，第一次取出白球的概率为4/7。第二步，由题意取出白球后会再放入2个白球，球的总数为9。第二次取出黄球的概率为3/9=1/3，故第一次取出白球，第二次取出黄球的概率为4/7×1/3=4/21。因此，选择B选项。

  • 第17题：

    袋子中有若干黑球和白球。若取出一个黑球，则袋中黑球占总球数的



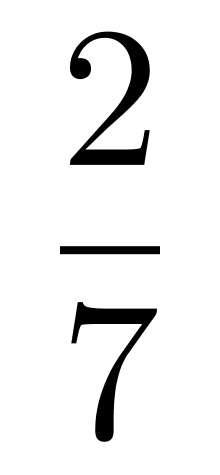
    ；若取出两个白球，则袋中白球占



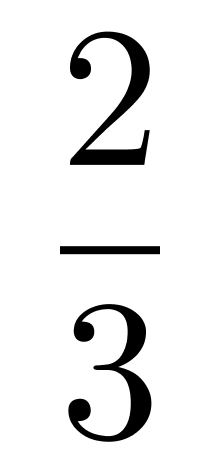
    。从原来袋中抽出3个球，其中有且仅有1个黑球的概率：

    A.低于20%
    B.在20%—40%之间
    C.在40%—60%之间
    D.高于60%

    答案：C
    解析：
    第一步，本题考查概率问题，用方程法解题。

  • 第18题：

    袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X、Y、Z分别表示两次取球所取得的红、黑与白球的个数。①求②求二维随机变量(X,Y)的概率分布。


    答案：
    解析：

  • 第19题：

    袋中有8个乒乓球，其中5个白色球，3个黄色球，从中一次任取2个乒乓球，则取出的2个球均为白色球的概率为《》（ ）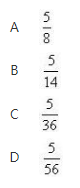


    答案：B
    解析：

  • 第20题：

    袋中有l个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球，以X，y，Z分别表示两次取球所取得的红球、黑球与白球的个数。
    (1)求
    (2)求二维随机变量(X，Y)的概率分布。


    答案：
    解析：

  • 第21题：

    一布袋中有红球8个，白球5个和黑球12个，它们除颜色外没有其他区别，随机地从袋中取出1球不是黑球的概率为（ ）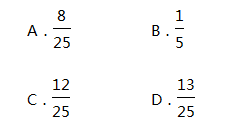


    答案：D
    解析：

  • 第22题：

    一口袋有6个白球，4个红球，“无放回”地从袋中取出3个球，则事件“恰有两个红球”的概率为（）


    正确答案:3/10

  • 第23题：

    填空题
    一袋中有50个乒乓球，其中20个红球，30个白球，今两人从袋中各取一球，取后不放回，则第二个人取到红球的概率为____。

    正确答案： 2/5
    解析：
    设A：“第一个人取红球”，B：“第二个人取红球”，则
    P（B）＝P[B（A∪A(＿)）]＝P（AB）＋P（A(＿)B）＝P（B|A）P（A）＋P（B|A(＿)）P（A(＿)）＝（19/49）×（20/50）＋（20/49）×（30/50）＝2/5

相关内容