设矩阵，.当a为何值时，方程AX=B无解、有唯一解、有无穷多解？在有解时，求解此方程.

题目
设矩阵，.
　　当a为何值时，方程AX=B无解、有唯一解、有无穷多解？在有解时，求解此方程.

相似考题

1.设，则A的转置矩阵A'=( )。

2.设A,B为正定矩阵,C是可逆矩阵,下列矩阵不是正定矩阵的是().

3.设A,B为n阶对称矩阵,下列结论不正确的是().A.AB为对称矩阵 B.设A,B可逆,则A^-1+B^-1为对称矩阵 C.A+B为对称矩阵 D.kA为对称矩阵

4.设A为矩阵，都是线性方程组Ax=0的解，则矩阵A为：

更多“设矩阵，. ”相关问题

  • 第1题：

    设A是一个n阶矩阵，那么是对称矩阵的是（ ）.



    答案：A
    解析：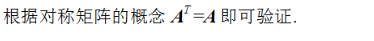

  • 第2题：

    设A为m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r1，矩阵B=AC的秩为r，则



    答案：C
    解析：

  • 第3题：

    设A为m×n矩阵，B为s×n矩阵.证明：.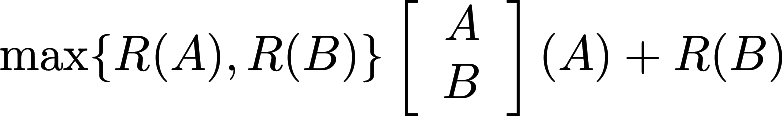


    答案：
    解析：

  • 第4题：

    设A为n阶对称矩阵，k为常数.试证kA仍为对称矩阵.


    答案：
    解析：

  • 第5题：

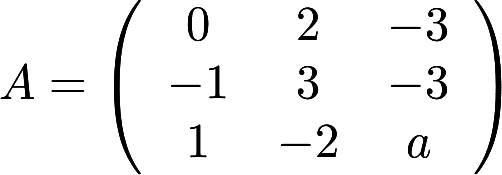    设矩阵相似于矩阵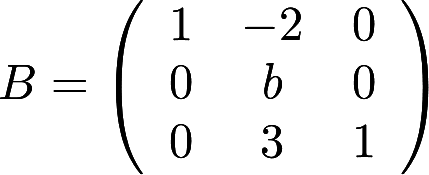. （1）求a,b的值；（2）求可逆矩阵P，使为对角阵


    答案：
    解析：

  • 第6题：

    设A为n阶正定矩阵,证明：对任意的可逆矩阵P,P^TAP为正定矩阵.


    答案：
    解析：

  • 第7题：

    设A,B为n阶正定矩阵.证明：A+B为正定矩阵.


    答案：
    解析：

  • 第8题：

    设A，B为三阶矩阵，且满足方程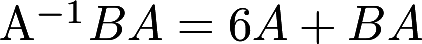.若矩阵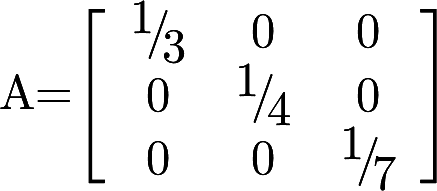,求矩阵B.


    答案：
    解析：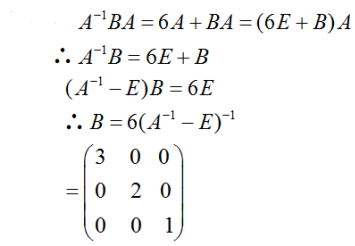

  • 第9题：

    设矩阵与等价，则a＝


    答案：
    解析：

  • 第10题：

    设N阶矩阵A与对角矩阵合同,则A是().

    A.可逆矩阵
    B.实对称矩阵
    C.正定矩阵
    D.正交矩阵

    答案：B
    解析：

  • 第11题：

    设矩阵，则A^3的秩为________


    答案：
    解析：

  • 第12题：

    设矩阵是4阶非零矩阵, 且满足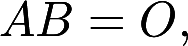证明矩阵B的秩


    答案：
    解析：

  • 第13题：

    设A为n×1矩阵，矩阵.试证B为对称矩阵.如果A=(1，-1，2)T，求B.


    答案：
    解析：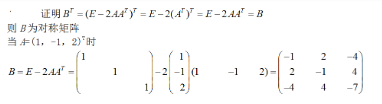

  • 第14题：

    设矩阵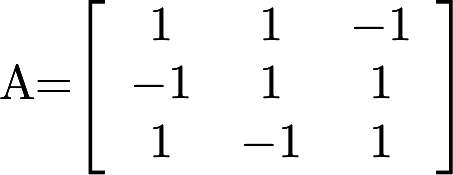，矩阵X满足，其中是A的伴随矩阵，求X.


    答案：
    解析：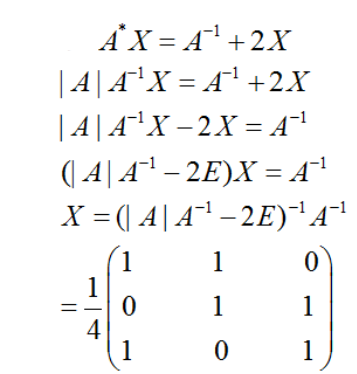

  • 第15题：

    设A、B、C为同阶矩阵，且C为非奇异矩阵，满足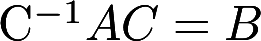，求证：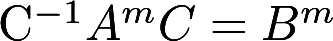


    答案：
    解析：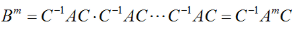

  • 第16题：

    设A是n阶矩阵，E+A是可逆矩阵，记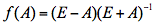，若A按足条件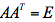，证明是反对称矩阵。


    答案：
    解析：


  • 第17题：

    设P为可逆矩阵,A=P^TP.证明：A是正定矩阵.


    答案：
    解析：

  • 第18题：

    设A为4阶魔术矩阵，分别对A进行如下操作： 求矩阵A的逆； 求矩阵A的行列式； 求矩阵A的秩； 求矩阵A的迹；


    正确答案: >>A=magic（4）
    >>B=inv（A）
    >>C=det（A）
    >>D=rank（A）
    >>E=trace（A）

相关内容