10件产品中4件为次品,6件为正品,现抽取2件产品.(1)求第一件为正品,第二件为次品的概率;(2)在第一件为正品的情况下,求第二件为次品的概率;(3)逐个抽取,求第二件为正品的概率.
题目
(1)求第一件为正品,第二件为次品的概率;
(2)在第一件为正品的情况下,求第二件为次品的概率;
(3)逐个抽取,求第二件为正品的概率.
相似考题
参考答案和解析

更多“10件产品中4件为次品,6件为正品,现抽取2件产品. ”相关问题
-
第1题:
事件A为“随机抽取3件产品,且至少有一件是正品”,事件B为“随机抽取3件产品,且有两件正品一件次品”,那么( )。
A.事件A与事件B互不相容
B.事件A与事件B互相独立
C.事件A与事件B互相对立
D.事件A包含事件B
正确答案:D
解析:记正品为“1”,次品为“0”,则事件A“随机抽取3件产品,且至少有一件是正品”的样本空间Ω={(1,1,1),(1,1,0),(1,0,1),(0,1,1),(1,0,0),(0,1,0),(0,0,1)};事件B“随机抽取3件产品,且有两件正品一件次品”的样本空间Ω={(1,1,0),(1,0,1),(0,1,1)},所以事件B中任一个样本点必在A中,故事件A包含事件B。 -
第2题:
:一个工人加工一批产品,他每加工出一件正品,得报酬0.75元,每加工出一件次品,罚款1.50元。这天他加工的正品是次品的7倍,得款11.25元。那么他这天加工出多少件次品?( )
A.1
B.3
C.7
D.13
正确答案:B工人加工7件正品得款0.75×7=5.25(元),加工出一件次品罚款1.50元,所以每加工8件产品得款5.25-1.50=3.75(元)。所以他这天加工出的次品是11.25÷3.75=3(件)。 -
第3题:
● 某轴承厂有甲、 乙、 丙三个车间,各车间生产的轴承数量分别占全厂的40%、 30%、30%,各车间的次品率分别为3%、4%、5%(正品率分别为97%、96%、95%)。以上叙述可以图示如下。
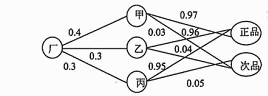
在图中,从“厂”结点出发选择三个车间产品的概率分别为 0.4、0.3、0.3,从各“车间”结点出发选择“正品”或“次品”的概率如图所示。从“厂”结点出发,到达“正品”(或“次品”)结点,可以有多条路径。例如,路径“厂—甲—次品”表示该厂甲车间生产的次品,其概率 P(厂—甲—次品)应等于各段上的概率之积。而该厂总的次品率应等于从“厂”结点到达“次品”结点的所有路径算出的概率之和(全概率公式)。而其中每条路径算出的概率在总概率中所占的比例,就是已知抽取产品结果再推测其来源(路径)
的概率(逆概率公式)。根据以上描述,可以算出,该厂的正品率约为 (53) 。如果上级抽查取出了一个次品,那么,该次品属于甲车间生产的概率约为 (54) 。
(53)
A. 0.963
B. 0.961
C. 0.959
D. 0.957
(54)
A. 0.25
B. 0.28
C. 0.31
D. 0.34
正确答案:B,C
-
第4题:
从一批有10件正品及2件次品的产品中,不放回地一件一件地抽取产品,设每个产品被抽到的可能性相同,求直到取出正品为止所需抽取的次数X的概率分布。答案:解析:由题意,x的所有可能的取值为1,2,3,
-
第5题:
设一批产品的次品率为p,为发现一件次品,至少检查2件的概率为答案:解析:
-
第6题:
甲箱中有5个正品,3个次品;乙箱中有4个正品,3个次品。从甲箱中任取3个产品放入乙箱,然后从乙箱中任取1个产品,则这个产品是正品的概率为( )。
A. 0. 176 B. 0. 2679 C. 0. 3342 D. 0. 5875答案:D解析:设B={从乙箱中取得正品},A1={从甲箱中取出3个正品},A2={从甲箱中取出2个正品1个次品},A3={从甲箱中取出1个正品2个次品},A4 ={从甲箱中取出3 个次品},显然A1、A2、A3、A4都是互斥的,所以B=B(A1 + A2+ A3+ A4)。

P(B A1) =7/10,P(B A2) =6/10,P(B A3) =5/10,P(B A4) =4/10;
故P(B) =P(BA1+BA2 + BA3+ BA4) =P(A1)P(B A1) +P(A2)P(B A2) +P(A3)P (B A3) +P(A4)P(B A4) = (10/56) x (7/10) + (30/56) x (6/10) + (15/56) x (5/ 10) + (1/56) x (4/10) =0.5875。 -
第7题:
一批产品有10个正品2个次品,任意抽取两次,每次取一个,抽取后不放回,求第二次抽取次品的概率.答案:解析:【解】令A1={第一次抽取正品},A2={第一次抽取次品},B={第二次抽取次品},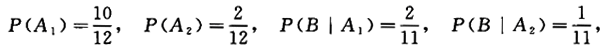
由全概率公式得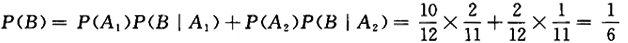
注解 不放回抽取的情况下,第一次抽取的结果未知时,第二次抽取某种产品的概率与第一次抽取的概率相同。 -
第8题:
已知一批产品的次品率为4%,从中有放回地抽取5个,则5个产品中没有次品的概率为()
- A、0.815
- B、0.17
- C、0.014
- D、0.999
正确答案:A -
第9题:
设工厂A和工厂B的产品的次品率分别为1%和2%,现从由A和B的产品分别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品属于A生产的概率是().
正确答案:3/7 -
第10题:
如果100件产品中,有10件次品,不放回地从中接连抽取两次,每次抽取一件,则第二次取到次品的概率是1/10
正确答案:正确 -
第11题:
设工厂A和工厂B的产品的次品率分别是1%和2%,现在从由A和B的产品分别是60%和40%的产品中随机抽取一件,发现是次品,则该次品属于A生产的概率是()
- A、2/7
- B、3/7
- C、2/9
- D、1/5
正确答案:B -
第12题:
单选题已知一批产品的次品率为4%,从中有放回地抽取5个,则5个产品中没有次品的概率为()A0.815
B0.17
C0.014
D0.999
正确答案: A解析: 暂无解析 -
第13题:
某轴承厂有甲、乙、丙三个车间,各车间生产的轴承数量分别占全厂的40%、30%、 30%,各车间的次品率分别为3%、4%、5%(正品率分别为97%、96%、95%)。以上叙述如下图所示。
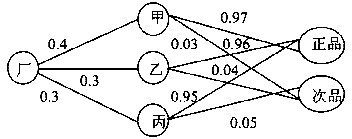
在图中,从“厂”结点出发选择三个车间产品的概率分别为0.4、0.3、0.3,从各“车间”结点出发选择“正品”或“次品”的概率如图所示。从“厂”结点出发,到达“正品”(或“次品”)结点,可以有多条路径。例如,路径“厂—甲一次品”表示该厂甲车间生产的次品,其概率P(厂一甲一次品)应等于各段上的概率之积。而该厂总的次品率应等于从“厂”结点到达“次品”结点的所有路径算出的概率之和(全概率公式)。而其中每条路径算出的概率在总概率中所占的比例,就是已知抽取产品结果再推测其来源(路径)的概率(逆概率公式)。根据以上描述,可以算出,该厂的正品率约为(53)。如果上级抽查取出了一个次品,那么该次品属于甲车间生产的概率约为(54)。
A.0.963
B.0.961
C.0.959
D.0.957
正确答案:B
-
第14题:
10个产品中有7个正品,3个次品,按不放回抽样,抽取2个产品,求两次都取到次品的概率是A.2/15
B.3/10
C.2/9
D.1/15
参考答案:D
-
第15题:
有10件产品,其中8件是正品,2件是次品.甲、乙两人先后各抽取1件产品,
求甲先抽到正品的条件下,乙抽到正品的概率.答案:解析:这是求在甲事件发生的条件下,乙事件发生的概率,故是条件概率.设A={甲抽到正品},B={乙抽到正品},所求为P(B|A).
解法l在缩小的样本空间中求条件概率,此时样本空间的样本点为9件产品中有7件正品,2件次品,所以


-
第16题:
设50件产品中,45件是正品,5件是次品,从中任取3件,求其中至少有l件
是次品的概率(精确到0.01).答案:解析:
-
第17题:
2012年3月15曰,某儿童玩具生产厂在对儿童玩具车的36件产品进行检验时,发现有4件次品,今从这36件产品中任取3件。
没有正品的概率为( )。
A. 0. 0006 B. 0.0007
C. 0. 0008
D. 0. 0009答案:A解析: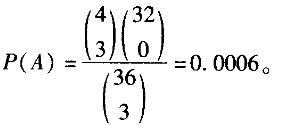
-
第18题:
已知一个箱子中装有12件产品,其中有2件次品。若从箱子中随机抽取2件产品进行检验,则恰好抽到1件次品的概率是: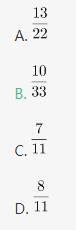 答案:B解析:第一步,本题考查概率问题。
答案:B解析:第一步,本题考查概率问题。
第二步,一个箱子装有12件产品,其中2件次品,则有12-2=10(件)非次品,随机抽出2件产品,恰好有1件次品,则抽出的另1件为非次品。那么抽出的2件产品恰好是1件次品1件非次品有
故抽取2件产品恰好有1件次品的概率为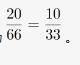
-
第19题:
一批产品共有十个正品和2个次品。任意抽取两次,每次抽取一个后不再放回。则第二次抽取的是次品的概率是()。
- A、1/5
- B、六分之一
- C、十一分之一
- D、十二分之一
正确答案:B -
第20题:
一批产品共有10个正品和2个次品,任意抽取两次,每次抽一个,抽出后不再放回,则第二次抽出的是次品的概率为().
正确答案:2/5 -
第21题:
某工厂的次品率为5%,并且正品中有80%为一等品,如果从该厂的产品中任取一件来检验,那么检验结果是一等品的概率为19/25
正确答案:正确 -
第22题:
接受概率L(P)=PO+P1+P3...=ΣP,式中PO的含义为()。
- A、样本合格数为0的抽取概率
- B、样本中不合格数为0的抽取概率
- C、产品中合格数为0的抽取概率
- D、产品中不合格数为0的抽取概率
正确答案:B -
第23题:
单选题一批产品共有十个正品和2个次品。任意抽取两次,每次抽取一个后不再放回。则第二次抽取的是次品的概率是()。A1/5
B六分之一
C十一分之一
D十二分之一
正确答案: C解析: 暂无解析
