设A为3×3矩阵,|A|=|-2|.把A按列分块为,其中是A的第j列.求 (1); (2).
题目
设A为3×3矩阵,|A|=|-2|.把A按列分块为 ,其中
,其中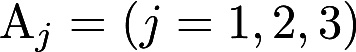 是A的第j列.求 (1)
是A的第j列.求 (1)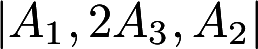 ; (2).
; (2).
 ,其中
,其中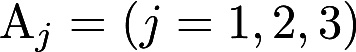 是A的第j列.求 (1)
是A的第j列.求 (1)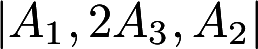 ; (2).
; (2).
相似考题
参考答案和解析
答案:
解析:

更多“设A为3×3矩阵,|A|=|-2|.把A按列分块为,其中是A的第j列.求 (1); (2).”相关问题
-
第1题:
设A是3阶方阵,将A的第1列与第2列交换得B,再把B的第2列加到第3列得C, 则满足AQ=C的可逆矩阵Q为
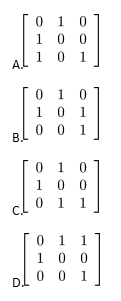 答案:D解析:
答案:D解析:
-
第2题:
设A是3阶矩阵,矩阵A的第1行的2倍加到第2行,得矩阵B,则下列选项中成立的是:A. B的第1行的一2倍加到第2行得A
B. B的第1列的一2倍加到第2列得A
C. B的第2行的一2倍加到第1行得A
D. B的第2列的一2倍加到第1列得A答案:A解析:由题目给出的运算写出行列式,验证还原到原行列式时应用哪一种运算方法。 -
第3题:
设为3阶矩阵,将的第2列加到第1列得矩阵,再交换的第2行与第3行得单位矩阵,记,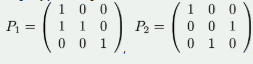 ,则A=( )
,则A=( )
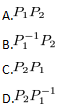 答案:D解析:
答案:D解析:
-
第4题:
设A为n阶非奇异矩阵,α为n维列向量,b为常数.记分块矩阵 .其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是.
.其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是. 答案:解析:
答案:解析: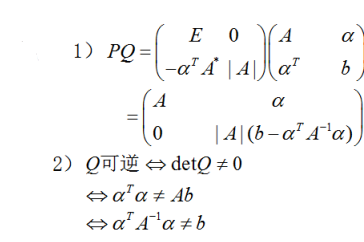
-
第5题:
设A是三阶实对称矩阵,r(A)=1,A^2-3A=O,设(1,1,-1)t为A的非零特征值对应的特征向量.(1)求A的特征值;(2)求矩阵A.答案:解析:
-
第6题:
设矩阵 ,α1,α2,α3为线性无关的3维列向量组,则向量组Aα1,Aα2,Aα3的秩为_________.答案:1、2.解析:因(Aα1,Aα2,Aα3)=A(α1,α2,α3),又α,α,α是三维线性无关列向量,所以(α1,α2,α3)为三阶可逆矩阵故r(Aα1,Aα2,Aα3)=r(A)=2.
,α1,α2,α3为线性无关的3维列向量组,则向量组Aα1,Aα2,Aα3的秩为_________.答案:1、2.解析:因(Aα1,Aα2,Aα3)=A(α1,α2,α3),又α,α,α是三维线性无关列向量,所以(α1,α2,α3)为三阶可逆矩阵故r(Aα1,Aα2,Aα3)=r(A)=2. -
第7题:
设A为3阶矩阵,将A的第2列加到第l列得矩阵曰,再将曰的第2行与第3行交换得 A. P1p2
A. P1p2
B.P-11 P2
C.P2P1
D.P2P一11答案:C解析:由于将A的第2列加到第l列得矩阵曰,
-
第8题:
问答题设A=[aij]3×3是三阶非零矩阵,而且满足aij=-Aij(i,j=1,2,3),其中Aij为行列式|A|中aij的代数余子式,求行列式|A|的值。正确答案:
由题中条件可知A*=-AT,则,A*,=,-AT,。由,A*,=,A,3-1=,A,2,,-AT,=(-1)3,A,,则,A,2=(-1)3,A,=-,A,,故,A,=0或,A,=-1。
因为矩阵A为非零矩阵,可设a11≠0,A的行列式为,A,=a11A11+a12A12+a13A13=-a112-a122-a132≠0,所以,A,=-1。解析: 暂无解析 -
第9题:
问答题请根据以下各小题的要求设计C应用程序(包括界面和代码)。 请编写函数fun(),它的功能是:将3行4列矩阵x乘以4行3列矩阵y,结果放在3行3列矩阵xy中。矩阵相乘的基本方法是:矩阵xy中行列下标分别为i,j的元素的值,是矩阵x中第i行上4个元素与矩阵y第j列上4个元素对应相乘的和。 注意:部分源程序给出如下。 请勿改动主函数main和其他函数中的任何内容,仅在函数fun的花括号中填入所编写的若干语句。 试题程序如下: #include#include void fun(int a[3][4],int b[4][3],int ab[3][3]) { } main() { int x[3][4] = {{1,0,1,1}, {2,1,0,1}, {1,2,0,3}}; int y[4][3] = {{1,1,1}, {0,0,0}, {2,1,1}, {1,1,3}}; int xy[3][3] = {0},i,j; fun(x,y,xy); printf(a × b = ab:(3,3):); for(i=0;i<3;i++) { for(j=0;j<3;j++) printf(%d,xy[i][j]); printf(); } } 正确答案:
void fun(int a[3][4],int b[4][3],int ab[3][3])
{
int j,k,l;
for(k=0;k<3;k++)
for(l=0;l<3;l++)
for(j=0;j<4;j++)
ab[k][l]+=a[k][j]*b[j][l];
}
解析: 本题首先要明确矩阵xy中行列下标分别为i,j的元素的值,是矩阵x中第i行上4个元素与矩阵y第j列上4个元素对应相乘再相加的和。因此,每个元素的求解是循环控制来实现的,即ab[k][l]+=a[k][j]*b[j][l],矩阵ab的每个元素的表示可用一个二重循环,整个函数是一个三重循环的嵌套。 -
第10题:
设A为3阶矩阵,将A的第2行加到第1行得B,再将B的第1列的-1倍加到第2列得C,记 ,则( ?)
,则( ?)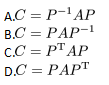 答案:B解析:
答案:B解析:
-
第11题:
设A是3阶方阵,将A的第1列与第2列交换得B,再把B的第2列加到第3列得C,则满足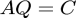 的可逆矩阵Q为( ?).
的可逆矩阵Q为( ?).
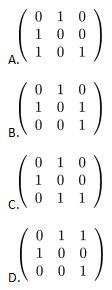 答案:D解析:
答案:D解析:
-
第12题:
设A为n(n≥2)阶可逆矩阵,交换A的第1行与第2行得矩阵B,分别为A,B的伴随矩阵,则( )。A.交换A的第1列与第2列得B
B.交换A的第1行与第2行得B
C.交换A的第1列与第2列得-B
D.交换A的第1行与第2行得-B答案:C解析: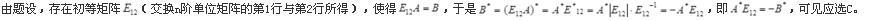
-
第13题:
设A是3阶矩阵,交换A的1,2列得B,再把B的第2 列加到第3 列上,得C.求Q,使得C=AQ.答案:解析:
-
第14题:
设矩阵A=
(1)已知A的一个特征值为3,试求y;
(2)求可逆矩阵P,使(AP)^T(AP)为对角矩阵.答案:解析:
-
第15题:
已知二次型f(x1,x2,3x)=x^TAx在正交变换x=Qy下的标准形为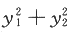 ,且Q的第3列为
,且Q的第3列为 .
.
(Ⅰ)求矩阵A;
(Ⅱ)证明A+E为正定矩阵,其中E为三阶单位矩阵.答案:解析:
-
第16题:
会统模块报表小计计算项公式U(1,3)=R(2_5)的含义是()。
- A、第1行第3列单元格由第3行第2至5列求和得到
- B、第1行第3列单元格由第3列第2至5行求和得到
- C、以第1行第3列单元格为基准数,调整第3行第2至5列
- D、以第1行第3列单元格为基准数,调整第3列第2至5行
正确答案:B -
第17题:
单选题设A是3阶矩阵,矩阵A的第1行的2倍加到第2行,得矩阵B,则以下选项中成立的是()。AB的第1行的-2倍加到第2行得A
BB的第1列的-2倍加到第2列得A
CB的第2行的-2倍加到第1行得A
DB的第2列的-2倍加到第1列得A
正确答案: C解析: 暂无解析 -
第18题:
单选题设A是m×n矩阵,A以列分块,记A=(α(→)1,α(→)2,…,α(→)n),在A中划去第i列得到的矩阵记为B,B=(α(→)1,…,α(→)i-1,α(→)i+1,…,α(→)n),则r(A)=r(B)是α(→)i可以由B的列向量线性表示的( )。A充分条件
B必要条件
C充要条件
D既不充分又不必要条件
正确答案: C解析:
若r(A)=r(B),则B的列向量组的极大线性无关组也是A的列向量组的极大线性无关组,而αi不在其中,故αi可以由B的列向量的极大线性无关组线性表示。
反之,若αi可以由B的列向量组线性表示,且A的其余列向量也可以由B是列向量组线性表示,故A是列向量组与B的列向量组等价,故r(A)=r(B)。
