利用矩阵的初等变换,求方阵的逆
题目
利用矩阵的初等变换,求方阵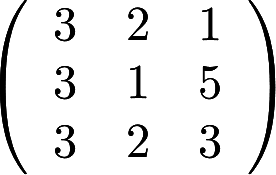 的逆
的逆
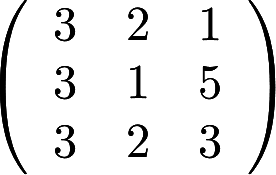 的逆
的逆相似考题
更多“ 利用矩阵的初等变换,求方阵的逆”相关问题
-
第1题:
初等矩阵( )A.都可以经过初等变换化为单位矩阵
B.所对应的行列式的值都等于1
C.相乘仍为初等矩阵
D.相加仍为初等矩阵答案:A解析:
-
第2题:
N阶矩阵A经过若干次初等变换化为矩阵B,则().A.|A|=|B|
B.|A|≠|B|
C.若|A|=0则|B|=0
D.若|A|>0则|B|>0答案:C解析: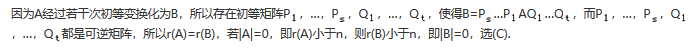
-
第3题:
已知 ,求作可s逆矩阵P,使得
,求作可s逆矩阵P,使得 是对角矩阵。答案:解析:
是对角矩阵。答案:解析:
-
第4题:
设A是n阶可逆方阵,将A的第i行和第j行对换后得到的矩阵记为B.
(1)证明B可逆;
(2)求AB^-1.答案:解析:
-
第5题:
设A是n阶可逆方阵,将A的第i行和第j行对换后得到的矩阵记为B, (1)证明B可逆; (2)求.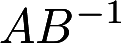 答案:解析:
答案:解析:
-
第6题:
利用逆矩阵解矩阵方程 。答案:解析:
。答案:解析:
-
第7题:
设A为n阶方阵,B是A经过若干次矩阵的初等变换后所得到的矩阵,则有( ).《》( ) 答案:C解析:
答案:C解析:
-
第8题:
det()用于矩阵求逆。
正确答案:错误 -
第9题:
设A为4阶魔术矩阵,分别对A进行如下操作: 求矩阵A的逆; 求矩阵A的行列式; 求矩阵A的秩; 求矩阵A的迹;
正确答案: >>A=magic(4)
>>B=inv(A)
>>C=det(A)
>>D=rank(A)
>>E=trace(A) -
第10题:
判断题det()用于矩阵求逆。A对
B错
正确答案: 错解析: 暂无解析 -
第11题:
单选题设A为n阶方阵,B是A经过若干次矩阵的初等变换后所得到的矩阵,则有( )。A|A|=|B|
B|A|≠|B|
C若|A|=0,则一定有|B|=0
D若|A|>0,则一定有|B|>0
正确答案: A解析:
矩阵A经过若干次初等变换后得到矩阵B,则存在可逆矩阵P,Q使得B=PAQ,因此|B|=|PAQ|=|P|·|A|·|Q|,若|A|=0,则必有|B|=|P|·|A|·|Q|=0成立。 -
第12题:
填空题求可逆矩阵A的逆矩阵的指令是()正确答案: inv(A)解析: 暂无解析 -
第13题:
设a为N阶可逆矩阵,则( ).
A.若AB=CB,则a=C
B.
C.A总可以经过初等变换化为单位矩阵E
D.以上都不对答案:C解析: -
第14题:
设矩阵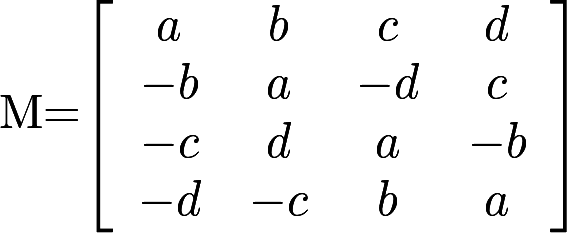 (a,b,c,d均为实数)(1)计算
(a,b,c,d均为实数)(1)计算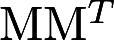 ;(2)利用(1)的结果,求detM.答案:解析:
;(2)利用(1)的结果,求detM.答案:解析: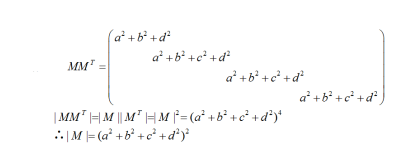
-
第15题:
设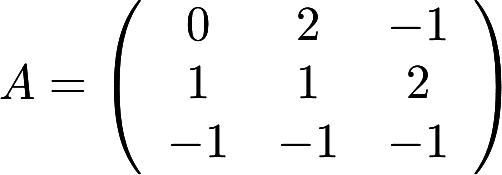 ,用初等行变换的方法求A的逆矩阵.然后据此将A分解成初等矩阵的乘积.答案:解析:
,用初等行变换的方法求A的逆矩阵.然后据此将A分解成初等矩阵的乘积.答案:解析:
-
第16题:
求下面分块矩阵的逆矩阵: 答案:解析:
答案:解析: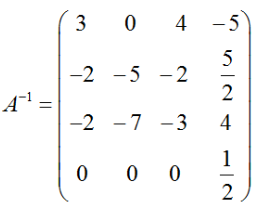
-
第17题:
设A为三阶方阵,A*为矩阵A的伴随矩阵, ,请计算
,请计算 答案:解析:
答案:解析:

-
第18题:
利用逆矩阵,解线性方程组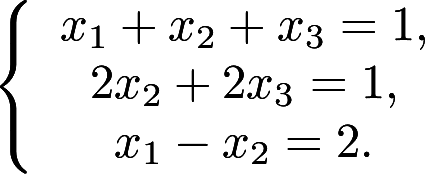 答案:解析:
答案:解析:
-
第19题:
矩阵A在( )时秩改变.A.转置
B.初等变换
C.乘以奇异矩阵
D.乘以非奇异矩阵答案:C解析: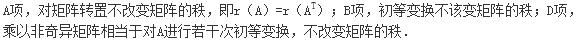
-
第20题:
求可逆矩阵A的逆矩阵的指令是()
正确答案:inv(A) -
第21题:
问答题设A为4阶魔术矩阵,分别对A进行如下操作: 求矩阵A的逆; 求矩阵A的行列式; 求矩阵A的秩; 求矩阵A的迹;正确答案: >>A=magic(4)
>>B=inv(A)
>>C=det(A)
>>D=rank(A)
>>E=trace(A)解析: 暂无解析 -
第22题:
问答题设A是n阶方阵,AAT=E,|A|<0,求|A+E|,其中AT是A的转置矩阵。正确答案:
因为AAT=E,所以,A+E,=,A+AAT,=,A(E+AT),=,A,·,E+AT,=,A,·,E+A,,整理得,,A+E,(1-,A,)=0。由,A,<0,知1-,A,≠0,故,A+E,=0。解析: 暂无解析 -
第23题:
单选题矩阵A在( )时秩改变。A转置
B初等变换
C乘以奇异矩阵
D乘以非奇异矩阵
正确答案: B解析:
A项,对矩阵转置不改变矩阵的秩,即r(A)=r(AT);
B项,初等变换不该变矩阵的秩;
D项,乘以非奇异矩阵相当于对A进行若干次初等变换,不改变矩阵的秩。
