在下图中，大正方形的边长为10,连接大正方形的各边中点得到小正方形，将小正方 形每边三等分，再将三等分点与正方形的中心和对应的顶点相连，得到如下图形。那么阴影部分面积是（）。

题目
在下图中，大正方形的边长为10,连接大正方形的各边中点得到小正方形，将小正方 形每边三等分，再将三等分点与正方形的中心和对应的顶点相连，得到如下图形。那么阴影部分面积是（）。


相似考题

1.表示表面为正方形时,可选择如下那种表示法?( )A写上“正方形”B边长×边长C□D标注总面积

2.（8）正方形边长为1，以各个顶点半径为1做弧，在正方形中间有一个公共区域，求面积。

3.把一个正方形的一边减少2cm，另一边增加20%，得到一个长方形，它与原来的正方形面积相等，那么，正方形的边长是( )。m。A．13B．10C．12D．15

4.画一个边长为2cm的正方形，再以这个正方形的对角线为边画第二个正方形，再以第二个正方形的对角线为边画第三个正方形，则第三个正方形面积为（ ）平方厘米。A.32B.16C.8D.4

更多“在下图中，大正方形的边长为10,连接大正方形的各边中点得到小正方形，将小正方 形每边三等分，再将三等分点与正方形的中心和对应的顶点相连，得到如下图形。那么阴影部分面积是（）。 ”相关问题

  • 第1题：

    把一个正方形的一边减少20%，另一边增加2米。得到一个长方形，它与原正方形的面积相等，那么，正方形面积是多少平方米？（ ）

    A．8

    B．10

    C．16

    D．64


    正确答案：D
    设正方形的边长为a，则正方形的面积为a2=(a+2)·a·(1-20%),解方程得a=8，则正方形的面积为64，所以D项为正确答案。

  • 第2题：

    如图中，两个小正方形的周长和是8分米，则大正方形的边长是____分米。


    正确答案：2

  • 第3题：

    如下图所示，大正方形周长比小正方形周长多 80，阴影部分的面积为 880，大正方形 面积是：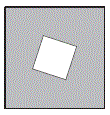

    A.144
    B.625
    C.900
    D.1 024

    答案：D
    解析：
    大正方形周长比小正方形多80，则边长多20，设小正方形边长为x，大正方形为x+20。（ｘ＋20）2-x2=880，解得x=12。大正方形面积为880+122=1024。

  • 第4题：

    依序连接正方形各边的中点得到新的正方形，如此反复三次。阴影部分与空白部分的面积比为( )



    A. 3:1
    B. 3:2
    C. 5:3
    D. 5:2

    答案：C
    解析：
    解题指导： 答案为C。

  • 第5题：

    把一个正方形的一边减少20%，另一边增加2米。得到一个长方形，它与原正方形的面积相等，那么，正方形面积是多少平方米?( )

    A. 8
    B. 10
    C. 16
    D. 64

    答案：D
    解析：
    设正方形的边长为a，则正方形的面积为a2=(a+2)*a*(1-20%),解方程得a=8，则正方形的面积为64。故答案为D。

  • 第6题：

    如图，有大小两个正方形，其对应边的距离均为1厘米。如果两个正方形之间部分的面积是20平方厘米，那么，小正方形的面积是多少平方厘米？（ ）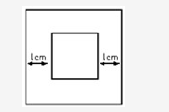


    A4
    B9
    C16
    D25


    答案：C
    解析：
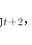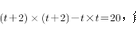    设小正方形的边长为，则大正方形的边长为，依题意有，解之得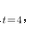，所以面积为16。

    故正确答案为C。

  • 第7题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )
    A. 11.75 B. 16.45 C. 19.625 D. 39. 25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10x10x2，所以大半圆的面积是1/2x1/4xπx10x10x2=25π（平方厘米）；
    小半圆的面积是π/2X5X5 = 12. 5π（平方厘米）；
    阴影的面积是25π-12. 5π=12. 5π=39. 25（平方厘米）。
    故本题选D。

  • 第8题：

    如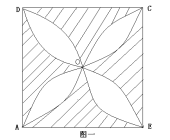，四边形ABCD是边长为1的正方形，弧AOB，BOC，COD，DOA均为半圆，则阴影部分的面积为



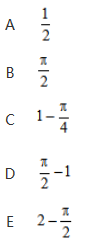    答案：E
    解析：

  • 第9题：

    如图所示，大正方形周长比小正方形周长多 80，阴影部分的面积为 880，大正方形面积是：


    A.144
    B.625
    C.900
    D.1024

    答案：D
    解析：
    大正方形周长比小正方形多80，则边长多20，设小正方形边长为x，大正方形为x+20。（ｘ＋20）2-x2=880，解得x=12。大正方形面积为880+122=1024。

  • 第10题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )

    A. 11.75 B. 16.45 C. 19.625 D. 39.25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。
    由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10X10X2，所以大半圆的面积是1/2x1/4xπx10x10x2 = 25π(平方厘米)；
    小半圆的面积是1/2πx5x5 = 12. 5π(平方厘米)；
    阴影的面积是25π-12. 5π=12. 5π=39. 25(平方厘米)。
    故本題选D。

  • 第11题：

    图形面积相等的圆、正方形，给人的感觉正方形大而圆面积小。


    正确答案:正确

  • 第12题：

    单选题
    己知正方形的边长，求正方形的周长和面积，经过一下几个步骤，正确的顺序为（） ①输入正方形的边长 ②计算正方形的周长 ③计算正方形的面积 ④输出周长及面积
    A

    ①②③④

    B

    ②①③④

    C

    ②③①④

    D

    ②③④①


    正确答案： A
    解析： 暂无解析

  • 第13题：

    一个正方形的一边减少20%，另一边增加2，得到长方形的面积与原正方形的面积相等，问正方形面积是多少?

    A．8

    B．10

    C．16

    D．64


    正确答案：D
    [答案] D。解析：设正方形的边长为x，(1-20%)×(x+2)=x2,x=8。原正方形的面积为64。

  • 第14题：

    下图中，每个小正方形网格都是边长为1的小正方形，则阴影部分面积最大是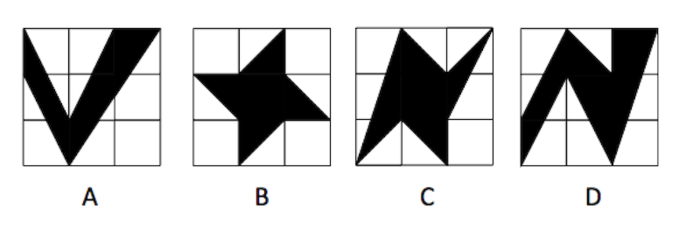： AA
    BB
    CC
    DD


    答案：D
    解析：
    解析:
    根据题目所给图形，可计算得：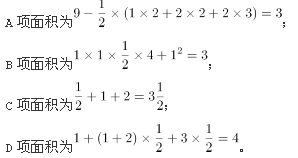

    故正确答案为D。

  • 第15题：

    在下图中，大正方形的边长为10，连接大正方形的各边中点得到小正方形，将小正方形 每边三等分，再将三等分点与正方形的中心和对应的顶点相连，得到如下图形。那么阴影部分 面积是（）。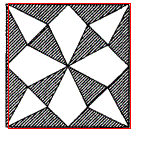


    A.25
    B.100/3
    C.50
    D.75

    答案：C
    解析：
    将小正方形内部的阴影部分沿着对应的小正方形边向外翻折，可以将原图转化为如下 图所示的样子，因此阴影部分面积为10x10+2=50。

  • 第16题：

    如图所示，一个边长为16厘米的大正方形，在距离角一定位置处与对角线平行折叠四次，得到中部小正方形的边长为4厘米。如果CB与大正方形的对边平行，则三角形ABC的面积为（ ）。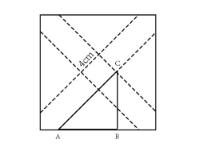

    A.32
    B.16
    C.16
    D.24

    答案：A
    解析：
    第一步，本题考查几何问题，属于平面几何类。
    第二步，如下图所示，由于正方形的对角线互相垂直且平分，过正方形的中心做平行于底边的一条线，容易看出这条线过C点（否则小正方形对角线将不能垂直平分）。可知BC长度为正方形边长的一半，即16÷2=8厘米。由中心是小正方形，则∠ABC是直角的一半即45°，可知△ABC是一个等腰直角三角形，面积为8×8÷2=32（平方厘米）。

  • 第17题：

    如图，将正方形边长三等分后可得9个边长相等的小正方形，把中间的小正方形去掉，对剩下的8个小正方形，均按上面方法操作。问：对一个边长为2的正方形如此操作三次后所剩白色区域的面积是多少？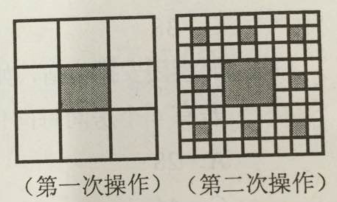

    A.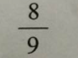
    B.
    C.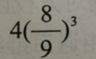
    D.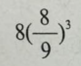

    答案：C
    解析：

  • 第18题：

    在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲，和L形区域乙、丙。已知三块区域甲、乙、丙的周长之比为4∶5∶7，并且区域丙的面积为48，求大正方形的面积：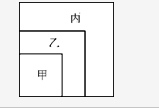

    A 96
    B 98
    C 200
    D 102


    答案：B
    解析：

  • 第19题：

    用边长为120cm的正方形铁皮做一个无盖水箱，先在四角分别截去一个边长相等的小正方形，然后把四边垂直折起焊接而成，问剪去的小正方形的边长为多少时，水箱容积最大最大容积是多少


    答案：
    解析：
    设剪去的小正方形边长为x(cm)，则水箱底边长为120-2x，则水箱容积为

    ∴剪去的小正方形边长为20cm时水箱容积最大为128000cm3．

  • 第20题：

    图6-18是一个边长为10的正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,则阴影部分的面积为（ ）




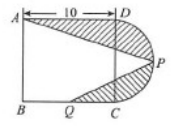
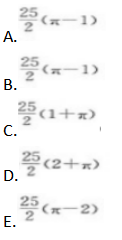    答案：C
    解析：

  • 第21题：

    图中的大正方形ABCD的面积是1平方厘米，其他点都是它所在边的中点。弧是一个内切于小正方形IJKL的半圆弧，PQ、OP是与弧半径相等的圆的四分之一圆弧，则阴影区的面积是多少平方厘米？（ ）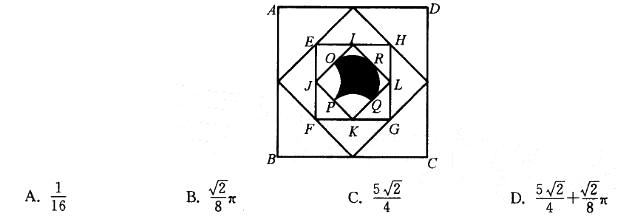


    答案：A
    解析：
    由正方形是大正方形面积的1/4，小正方形IJKL是正方形EFHG面积的1/2，故小正方形IJKL是大正方形ABCD面积的1/8，如下图所示，图中的阴影部分面积是小正方形IJKL 的一半，所以阴影区的面积为大正方形面积的1/16。A为正确选项。

  • 第22题：

    如图9所示的“勾股树”中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大正方形的边长为12cm，则A、B、C、D四个小正方形的面积之和为__________。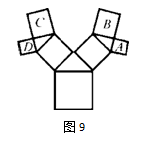


    答案：
    解析：
    144

  • 第23题：

    己知正方形的边长，求正方形的周长和面积，经过一下几个步骤，正确的顺序为（） ①输入正方形的边长 ②计算正方形的周长 ③计算正方形的面积 ④输出周长及面积

    • A、①②③④
    • B、②①③④
    • C、②③①④
    • D、②③④①

    正确答案:A

相关内容