（8）正方形边长为1，以各个顶点半径为1做弧，在正方形中间有一个公共区域，求面积。
题目
（8）正方形边长为1，以各个顶点半径为1做弧，在正方形中间有一个公共区域，求面积。
相似考题
更多“(8)正方形边长为1,以各个顶点半径为1做弧,在正方形中间有一个公共区域,求面积。 ”相关问题
-
第1题：
如图，将正方形边长三等分后可得9个边长相等的小正方形，把中间的小正方形去掉，对剩下的8个小正方形，均按上面方法操作。问：对一个边长为2的正方形如此操作三次后所剩白色区域的面积是多少？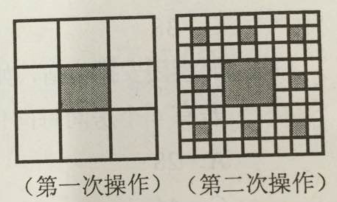
A.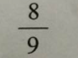
B.
C.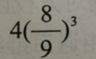
D.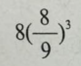
答案：C解析：
-
第2题：
一个半径为1厘米的圆在一个边长为8厘米的正方形内，沿正方形的边与边相切滚动过正方形一周。圆滚动覆盖的总面积为（ ）平方厘米。A.44
B.48
C.48－π
D.44＋π答案：D解析：第一步，本题考查几何问题，属于平面几何类。
第二步，如下图，阴影部分即为所求。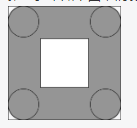
阴影部分的面积先去掉中间空白部分8×8－4×4＝48，再去掉四个角，四个角的面积为边长为2的正方形减去一个与其四边相切的圆，即2×2－π＝4－π，所以阴影部分面积为48－（4－π）＝44＋π（平方厘米）。 -
第3题：
2、设计一个Shape接口和它的两个实现类正方形Square和圆形Circle 1）Shape接口中有一个抽象方法area（），方法接收一个double类型的参数，返回一个double类型的结果。 2）Square和Circle中实现了Shape接口的area（）抽象方法，分别求正方形和圆形的面积并返回 3）分别创建Square和Circle对象，计算边长为2的正方形面积和半径为3的圆形面积
interface Shape { double area(double givenValue)}class Square implements Shape{ public double area(double sideLength) { return sideLength*sideLength }}class Circle implements Shape{ public double area(double r) { return Math.PI*r*r }}public class Test02 { public static void main(String[] args) { Shape square = new Square() Shape circle = new Circle() System.out.println(square.area(2)) System.out.println(circle.area(3)) }} -
第4题：
在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲，和L形区域乙、丙。已知三块区域甲、乙、丙的周长之比为4∶5∶7，并且区域丙的面积为48，求大正方形的面积：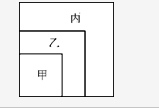
A 96
B 98
C 200
D 102答案：B解析：
-
第5题：
在2维的坐标系中，距离原点的ℓ_1范数距离（曼哈顿距离)等于1的点的轨迹是____。
A．以原点为中心，半径为1的圆
B．以原点为中心，边长为2，各个边与坐标轴平行的正方形
C．以原点为中心，以两个坐标轴为对角线，边长为根号2的正方形
D．以原点为中心，边长为根号2，各个边与坐标轴平行的正方形
以原点为中心，以两个坐标轴为对角线，边长为根号2的正方形