在边长为2的正方形内部,以A为圆心,AB为半径画弧,再以BC为直径画半圆。则两块阴影部分面积差的绝对值为:A.(π-2)/2 B.π-2 C.(5π-14)/2 D.(3π-8)/2
题目
在边长为2的正方形内部,以A为圆心,AB为半径画弧,再以BC为直径画半圆。则两块阴影部分面积差的绝对值为:
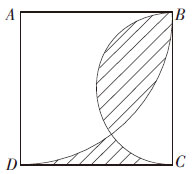

A.(π-2)/2
B.π-2
C.(5π-14)/2
D.(3π-8)/2
B.π-2
C.(5π-14)/2
D.(3π-8)/2
相似考题
更多“在边长为2的正方形内部,以A为圆心,AB为半径画弧,再以BC为直径画半圆。则两块阴影部分面积差的绝对值为: ”相关问题
-
第1题:
如图,在以AB为直径的半圆上取一点C,分别以AC和BC为直径在AABC外作半圆A£C和BFC。当C点在什么位置时,图中两个弯月形(阴影部分)AEC和BFC的面积和最大?( )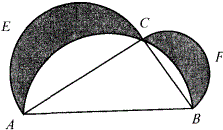 A. AC大于BC
A. AC大于BC
B. AC小于BC
C. AC等于BC
D.无法得出答案:C解析: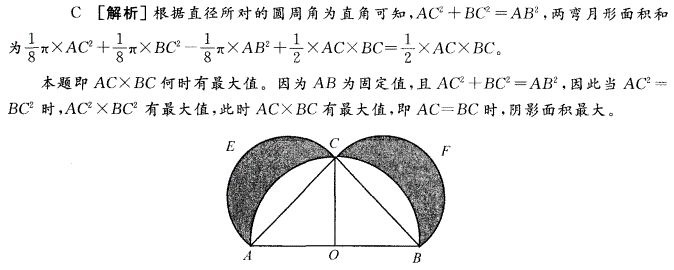
-
第2题:
某小区规划建设一条边长为10米的正方形绿地。如图所示,以绿地的2个顶点为圆心,边长为半径分别作扇形,把绿地划分为不同的区域。小区现准备在图中阴影部分种植杜鹃,则杜鹃种植面积为( )平方米。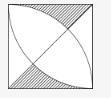 A.100-25π
A.100-25π
B.200-35π
C.200-50π
D.100π-100答案:A解析:第一步,本题考查几何问题,用割补平移法解题。
第二步,阴影部分为不规则图形,考虑割补平移解题,将左下方阴影部分平移到右上方的空白部分,则阴影面积为右上部分面积,即正方形面积-四分之一圆的面积。
第三步,正方形的面积为10×10=100(平方米),四分之一圆的面积为π×102÷4=25π(平方米),那么阴影部分的面积为(100-25π)平方米。
因此,选择A选项。 -
第3题:
如下图所示,正方形ABCD的边长为5cm,AC、BD分别是以点D和点C为圆心、 5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小多少?(π取3. 14)( )
A. 13.75cm2 B. 14. 25cm2
C. 14. 75cm2 D. 15. 25cm2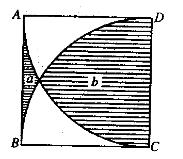 答案:B解析:几何问题,利用容斥原理进行求解。分析题干可知,两个1/4圆覆盖的区城面积减去阴影部分b的面积再加上阴影部分a的面积等于正方形的面积,所以得到1/4X3.14X52X2-b+a=52,b-a = 14.25(cm2)。
答案:B解析:几何问题,利用容斥原理进行求解。分析题干可知,两个1/4圆覆盖的区城面积减去阴影部分b的面积再加上阴影部分a的面积等于正方形的面积,所以得到1/4X3.14X52X2-b+a=52,b-a = 14.25(cm2)。 -
第4题:
如图6-15所示,正方形ABCD的对角线∣AC∣=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,则阴影部分的面积为( )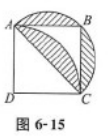 A.π-1
A.π-1
B.π-2
C.π+1
D.π+2
E.π答案:B解析:
-
第5题:
用半径为R的圆弧外切连接两个半径分别为R1,R2的圆弧.确定连接画弧圆心的方法为:分别以两己知圆弧的圆心O1,O2为圆心,以()为半径作圆弧,其交点即为连接弧的圆心O。
- A、R一Rl、R一RZ
- B、R+Rl、R+RZ
- C、Rl一R、RZ一R
- D、R一Rl、R+RZ
正确答案:B -
第6题:
足球罚球弧是以罚球点为圆心,()米为半径画弧,与罚球区线相交的一段弧线。
正确答案:9.15 -
第7题:
填空题棒球以()为中心,()米为半径画弧为内场线。正确答案: 投手板,28.93解析: 暂无解析 -
第8题:
填空题足球罚球弧是以罚球点为圆心,()米为半径画弧,与罚球区线相交的一段弧线。正确答案: 9.15解析: 暂无解析 -
第9题:
如图,Rt△ABC中,∠ABC=90o,AB=28 cm,以AB为直径的半圆与AC相交,图中的阴影部分①的面积比⑦的面积少28.28 cm2,求BC的长(π取3.14)。
 答案:解析:
答案:解析:
-
第10题:
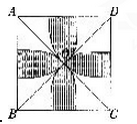
在边长为1的正方形ABCD中,AC与BD相交于O,以A、B、C、D分别为圆心,以对角线长的一半为半径画圆弧与正方形的边相交,如图,则图中阴影部分的面积为多少?(π=3.14)
 A.0.43
A.0.43
B.0.57
C.0.64
D.0.71答案:C解析:
-
第11题:
如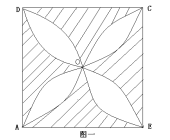 ,四边形ABCD是边长为1的正方形,弧AOB,BOC,COD,DOA均为半圆,则阴影部分的面积为
,四边形ABCD是边长为1的正方形,弧AOB,BOC,COD,DOA均为半圆,则阴影部分的面积为
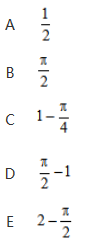 答案:E解析:
答案:E解析: -
第12题:
图6-18是一个边长为10的正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,则阴影部分的面积为( )
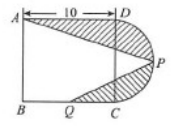
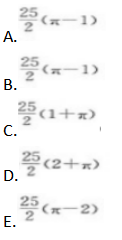 答案:C解析:
答案:C解析:
-
第13题:
抢道标志线的画法应为()
- A、以第三分界线上距内突沿外沿20厘米处为圆心,以直段长为半径向后画弧。
- B、以第三分界线上距内突沿外沿30厘米处为圆心,以直段长为半径向后画弧。
- C、以第三分界线上距内突沿外沿20厘米处为圆心,以100米长为半径向后画弧。
- D、以第三分界线上距内突沿外沿30厘米处为圆心,以100米长为半径向后画弧。
正确答案:B -
第14题:
球面度是一立体角,其顶点位于球心面,它在球面上所截取的面积等于()的面积。
- A、以球的半径为边长的正方形
- B、以球的半径为边长的等边三角形
- C、以球直径为边长的正方形
- D、以球直径为边长的等边三角形
正确答案:A -
第15题:
单选题球面度是一立体角,其顶点位于球心面,它在球面上所截取的面积等于()的面积。A以球的半径为边长的正方形
B以球的半径为边长的等边三角形
C以球直径为边长的正方形
D以球直径为边长的等边三角形
正确答案: C解析: 暂无解析 -
第16题:
单选题抢道标志线的画法应为()A以第三分界线上距内突沿外沿20厘米处为圆心,以直段长为半径向后画弧。
B以第三分界线上距内突沿外沿30厘米处为圆心,以直段长为半径向后画弧。
C以第三分界线上距内突沿外沿20厘米处为圆心,以100米长为半径向后画弧。
D以第三分界线上距内突沿外沿30厘米处为圆心,以100米长为半径向后画弧。
正确答案: C解析: 暂无解析
