设f（x）的一个原函数为1nx，则f（x）等于（ ）.《》（ ）

题目
设f（x）的一个原函数为1nx，则f（x）等于（ ）.《》（ ）

相似考题

1.设x2为f(x)的一个原函数，则f(x)=_______

2.设f(x)=则f{f［f(x)］)等于().

3.设F（x）是f（x）的一个原函数，则∫e-x f（e-x ）dx等于下列哪一个函数？ A.F（e-x）+c B.-F（e-x）+c C.F（ex）+c D.-F（ex）+c

4.设f(x)的一个原函数为x3，则xf(1-x2)dx=(57)。A．(1-x2)3+CB．C．D．x3+C

参考答案和解析
答案：A
解析：
更多“设f（x）的一个原函数为1nx，则f（x）等于（ ）.《》（ ） ”相关问题

  • 第1题：

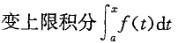    ，是下列中哪个函数？
    A.f'(x)的一个原函数 B.f'(x)的全体原函数
    C.f(x)的一个原函数 D.f(x)的全体原函数


    答案：C
    解析：
    提示:利用变上限函数的导数和f(x)关系确定。

  • 第2题：

    设f(x)的一个原函数是arctanx，则f(x)的导函数是（）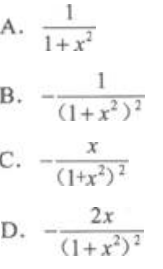


    答案：D
    解析：
    根据原函数的定义可知

  • 第3题：

    若cotx是f（x）一个原函数，则f（x）等于（ ）《》（ ）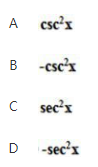


    答案：B
    解析：

  • 第4题：

    设x2是f(x)的一个原函数，则f(x)=（　　）


    答案：A
    解析：
    由于x2为f(x)的一个原函数，由原函数的定义可知f(x)=(x2)'=2x，故选A．

  • 第5题：

    设lnx是f(x)的一个原函数，则f'(x)=（　　）



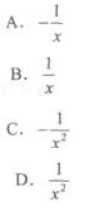    答案：C
    解析：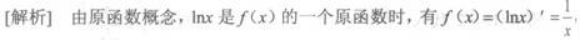

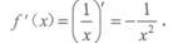
  • 第6题：

    设f（x）的一个原函数为cosx，g（x）的一个原函数为x2，则f［g（x）］等于：（）

    • A、cosx2
    • B、-sinx2
    • C、cos2x
    • D、-sin2x

    正确答案:D

  • 第7题：

    设f（x）在（-a，a）（a＞0）上连续，F（x）是f（x）的一个原函数，则当f（x）是奇函数时，下面结论正确的是（）。

    • A、F（x）是偶函数
    • B、F（x）是奇函数
    • C、F（x）可能是奇函数，也可能是偶函数
    • D、F（x）是否为奇函数不能确定

    正确答案:A

  • 第8题：

    设F（x），G（x）是f（x）的两个原函数，则下面的结论不正确的是（）。

    • A、F（x）+C也是f（x）的原函数，C为任意常数
    • B、F（x）=G（x）+C，C为任意常数
    • C、F（x）=G（x）+C，C为某个常数
    • D、F’（x）=G’（x）

    正确答案:B

  • 第9题：

    单选题
    设sinx/x为f（x）的一个原函数，且a≠0则∫[f（ax）/a]dx等于（　　）。
    A

    sinax/（a3x）＋C

    B

    sinax/（a2x）＋C

    C

    sinax/（ax）＋C

    D

    sinax/x＋C


    正确答案： A
    解析：
    ∫[f（ax）/a]dx＝∫f（ax）d（ax）/a2＝（1/a2）·sinax/（ax）＋C＝sinax/（a3x）＋C，故应选（A）。

  • 第10题：

    单选题
    设F（x）是f（x）的一个原函数，则∫e-xf（e-x）dx等于下列哪一个函数？（）
    A

    F（e-x）+c

    B

    -F（e-x）+c

    C

    F（ex）+c

    D

    -F（ex）+c


    正确答案： B
    解析： 暂无解析

  • 第11题：

    单选题
    设f′（lnx）=1+x，则f（x）等于（）
    A

    （1nx／2）（2+lnx）+c

    B

    x+（1／2）x2+c

    C

    x+ex+c

    D

    ex+（1／2）e2x+c


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    设F（x）是f（x）的一个原函数，则等于（）。
    A

    F（e-x）+C

    B

    -F（e-x）+C

    C

    F（ex）+C

    D

    -F（ex）+C


    正确答案： B
    解析： 暂无解析

  • 第13题：

    设F(x)是f(x)的一个原函数，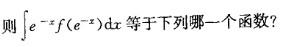
    A.F(e-x)+c B. -F(e-x)+c
    C.F(ex)+c D. -F(ex)+c


    答案：B
    解析：

  • 第14题：

    设f（x）的一个原函数为xln（x+l），则下列等式成立的是（ ）.《》（ ）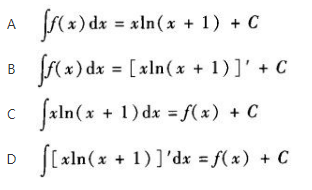


    答案：A
    解析：

  • 第15题：

    设F(x)是f(x)的一个原函数,则∫e-x f(e-x)dx等于( )。
    A. F(e-x) + C B. -F(e-x)+ C
    C. F(ex) + C D. -F(ex) +C


    答案：B
    解析：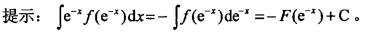

  • 第16题：

    设x是f(x)的一个原函数，则f(x)=



    答案：C
    解析：
    x为f(x)的一个原函数，由原函数定义可知f(x)=x'=1，故选C．

  • 第17题：

    设F（x）是f（x）的一个原函数，则∫e-xf（e-x）dx等于下列哪一个函数？（）

    • A、F（e-x）+c
    • B、-F（e-x）+c
    • C、F（ex）+c
    • D、-F（ex）+c

    正确答案:B

  • 第18题：

    设f′（lnx）=1+x，则f（x）等于（）

    • A、（1nx／2）（2+lnx）+c
    • B、x+（1／2）x2+c
    • C、x+ex+c
    • D、ex+（1／2）e2x+c

    正确答案:C

  • 第19题：

    设F（x）是f（x）的一个原函数，则等于（）。

    • A、F（e-x）+C
    • B、-F（e-x）+C
    • C、F（ex）+C
    • D、-F（ex）+C

    正确答案:B

  • 第20题：

    单选题
    设f（x）的一个原函数为cosx，g（x）的一个原函数为x2，则f［g（x）］等于：（）
    A

    cosx2

    B

    -sinx2

    C

    cos2x

    D

    -sin2x


    正确答案： A
    解析： 利用原函数定义，求出f（x）、g（x）；利用复合函数关系求出f[g（x）]。

  • 第21题：

    填空题
    设f（x）的一个原函数为xex，则∫xf′（x）dx＝____。

    正确答案： x2ex+C
    解析：
    采用分部积分法，∫xf′（x）dx＝∫xd[f（x）]＝xf（x）－∫f（x）dx，又由题意可知，f（x）＝（xex）′，则∫xf′（x）dx＝x（xex）′－xex＋C＝x2ex＋C。

  • 第22题：

    单选题
    设f（x）的一个原函数为xex，则∫xf′（x）dx＝（　　）。
    A

    xex＋C

    B

    x2ex＋C

    C

    －xex＋C

    D

    －x2ex＋C


    正确答案： C
    解析：
    采用分部积分法，∫xf′（x）dx＝∫xd[f（x）]＝xf（x）－∫f（x）dx，又由题意可知，f（x）＝（xex）′，则∫xf′（x）dx＝x（xex）′－xex＋C＝x2ex＋C。

  • 第23题：

    单选题
    设F（x），G（x）是f（x）的两个原函数，则下面的结论不正确的是（）。
    A

    F（x）+C也是f（x）的原函数，C为任意常数

    B

    F（x）=G（x）+C，C为任意常数

    C

    F（x）=G（x）+C，C为某个常数

    D

    F’（x）=G’（x）


    正确答案： D
    解析： 由原函数的定义有F’（x）=f（x），G’（x）=f（x），因此（D）正确，而（F（x）+C）’=f（x），因此（A）正确，F（x）=G（x）+C，C应为某个常数，因此（C）正确而（B）不正确。

相关内容