设三次函数 , 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是A.关于y轴对称 B.关于原点对称 C.关于直线y=x轴对称 D.以上均错

题目
设三次函数 , 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是

A.关于y轴对称
B.关于原点对称
C.关于直线y=x轴对称
D.以上均错
相似考题

1.以下命题正确的是()。A.不可导的点，一定不是该函数的极值点B.驻点或不可导的点有可能是函数的极值点C.驻点一定是极值点D.极值点一定是驻点

2.以下结论正确的是()。A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.

3.对于函数f(x),若f′(x0)=0,则x0是极值点。()此题为判断题(对，错)。

4.设f(x)=xe-x，求函数f(x)的极值（6分）

参考答案和解析
答案：B
解析：
更多“设三次函数 , 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是”相关问题

  • 第1题：

    设函数f(x)=ax3＋bx2＋cx＋d，问常数a，b，c满足什么关系时，f(x)分别没 有极值、可能有一个极值、可能有两个极值?


    正确答案：
    解



  • 第2题：

    函数厂（x）具有连续的二阶导数，且f″（0）≠0，则x=0（ ）。

    A.不是函数f（x）的驻点
    B.一定是函数f（x）的极值点
    C.一定不是函数f（x）的极值点
    D.是否为函数f（x）的极值点，还不能确定

    答案：D
    解析：
    由极值的必要条件可知，若f（x）在x=0处可导，且x=0是f（x）的极值点，则必有f′（0）=0。由题干无法确定f′（0）是否等于0，因此不能确定x=0是否为函数f（x）的极值点。

  • 第3题：

    设函数f(x，y)=X2+Y2+xy+3，求f(x，y)的极值点与极值．


    答案：
    解析：

  • 第4题：

    对于函数z=xy，原点(0，0)（）

    A.不是函数的驻点
    B.是驻点不是极值点
    C.是驻点也是极值点
    D.无法判定是否为极值点

    答案：B
    解析：
    【考情点拨】本题考查了函数的驻点、极值点的知识点．

  • 第5题：

    设z=z(x,y)是由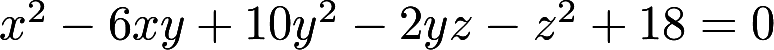 确定的函数，求 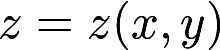的极值点和极值


    答案：
    解析：

  • 第6题：

    下列命题中，正确的是( ).

    A.单调函数的导函数必定为单调函数
    B.设f´(x)为单调函数，则f(x)也为单调函数
    C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点
    D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0

    答案：D
    解析：
    可导函数的极值点必定是函数的驻点，故选D.

  • 第7题：

    若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是（ ）。
    A. f(x,y)的极值点一定是f(x,y)的驻点
    B.如果P0是f(x,y)的极值点，则P0点处B2-AC)
    C.如果P0是可微函数f(x,y)的极值点，则P0点处df=0
    D.f(x,y)的最大值点一定是f(x,y)的极大值点


    答案：C
    解析：
    提示：如果P0是可微函数f(x,y)的极值点，由极值存在必要条件，在P0点处有

  • 第8题：

    设二元函数z=xy，则点Po(0，0)（）

    A.为z的驻点，但不为极值点
    B.为z的驻点，且为极大值点
    C.为z的驻点，且为极小值点
    D.不为z的驻点，也不为极值点

    答案：A
    解析：
    可知Po点为Z的驻点．当x、y同号时，z=xy>0；当x、y异号时，z=xy<0．在点Po(0，0)处，z|Po=0．因此可知Po不为z的极值点．因此选A．

  • 第9题：

    函数若在一个区域的内点处取到最值点，则它必是极值点。


    正确答案:正确

  • 第10题：

    函数的可微的极值点一定是驻点。


    正确答案:正确

  • 第11题：

    若函数f（x，y）在闭区域D上连续，下列关于极值点的陈述中正确的是（）。

    • A、f（x，y）的极值点一定是f（x，y）的驻点
    • B、如果P0是f（x，y）的极值点，则P0点处B2-AC<0
    • C、如果P0是可微函数f（x，y）的极值点，则P0点处df=0
    • D、f（x，y）的最大值点一定是f（x，y）的极大值点

    正确答案:C

  • 第12题：

    单选题
    设偶函数f（x）具有二阶连续导数，且f″（0）≠0，则x＝0（　　）。
    A

    一定不是函数的驻点

    B

    一定是函数的极值点

    C

    一定不是函数的极值点

    D

    不能确定是否为函数的极值点


    正确答案： D
    解析：
    由偶函数f（x）在x＝0处可导，可知f′（0）＝0。又f″（0）≠0，由第二充分条件得x＝0是极值点。

  • 第13题：

    二元函数在开区域内部如果只有一个极值点,则该极值点为最值点。()

    此题为判断题(对，错)。


    答案：错误

  • 第14题：

    若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是：
    A.f(x,y)的极值点一定是f(x,y)的驻点
    B.如果P0是f(x,y)的极值点，则P0点处B2-AC
    C.如果P0是可微函数f(x,y)的极值点，则在P0点处df=0
    D.f(x,y)的最大值点一定是f(x,y)的极大值点


    答案：C
    解析：
    提示:在题目中只给出f(x,y)在闭区域D上连续这一条件，并未讲函数f(x,y)在P0点是否具有一阶、二阶偏导，而选项A、B判定中均利用了这个未给的条件，因而选项A、B不成立。选项D中f(x,y)的最大值点可以在D的边界曲线上取得，因而不一定是f(x,y)的极大值点，故选项D不成立。
    在选项C中，给出p0是可微函数的极值点这个条件，因而f(x,y)在P0偏导存在，且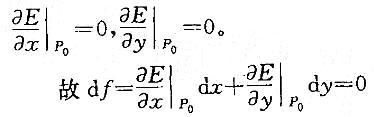

  • 第15题：

    下列命题正确的是（）

    A.函数f(x)的导数不存在的点，一定不是f(x)的极值点
    B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点
    C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)＝0
    D.若函数f(x)在点x0处连续，则f'(x0)一定存在

    答案：C
    解析：
    根据函数在点x0处取极值的必要条件的定理，可知选项C是正确的．

  • 第16题：

    函数f(x)在点xo处取得极值，则必有（　　）．



    答案：D
    解析：

  • 第17题：

    设函数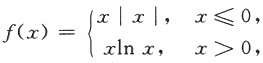则x=0是f(x)的

    A.A可导点，极值点B
    B.不可导点，极值点
    C.可导点，非极值点
    D.不可导点，非极值点

    答案：B
    解析：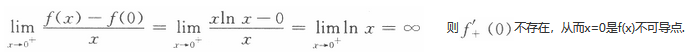

    又在x=0的左半邻域f(x)=x｜x｜<0=f(0)，
    　　在x=0的右半邻域f(x)=xln x<0=f(0)，
    　　则f(x)在x=0处取极大值，故应选(B).

  • 第18题：

    设函数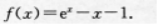
    (I)求f(χ)的单调区间；
    (Ⅱ)求f(χ)的极值．


    答案：
    解析：

  • 第19题：

    若函数处取得极值，则a的值是（ ）。


    答案：A
    解析：
    提示：由f(π/3)=0得到a的值。

  • 第20题：

    若某点为二元函数的极值点，则这点（）。

    • A、一定是函数的可微点
    • B、一定是函数的不可微点
    • C、一定是函数的驻点
    • D、或是驻点或是不可微点

    正确答案:D

  • 第21题：

    点x=0是函数y=x4的（）

    • A、驻点但非极值点
    • B、拐点
    • C、驻点且是拐点
    • D、驻点且是极值点

    正确答案:D

  • 第22题：

    由于函数极值点的必要条件是函数在这一点的（）的模为零，因此当迭代点的函数梯度的模已充分小时，则认为迭代可以终止。


    正确答案:梯度方向

  • 第23题：

    单选题
    若某点为二元函数的极值点，则这点（）。
    A

    一定是函数的可微点

    B

    一定是函数的不可微点

    C

    一定是函数的驻点

    D

    或是驻点或是不可微点


    正确答案： D
    解析： 暂无解析

相关内容