曲面xyz=1上平行于x+y+z+3=0的切平面方程是: A.x+y+z=0 B.x+y+z=1 C.x+y+z=2 D.x+y+z=3
题目
曲面xyz=1上平行于x+y+z+3=0的切平面方程是:
A.x+y+z=0
B.x+y+z=1
C.x+y+z=2
D.x+y+z=3
B.x+y+z=1
C.x+y+z=2
D.x+y+z=3
相似考题
更多“曲面xyz=1上平行于x+y+z+3=0的切平面方程是: ”相关问题
-
第1题:
设平面方程:x + y + z-1 = 0,直线的方程是1-x = y + 1=z,则直线与平面:
A.平行 B.垂直 C.重合 D.相交但不垂直答案:D解析:
-
第2题:
曲面z=1-x2-y2在点(1/2,1/2,1/2)处的切平面方程是:
A.x+y+z-3/2=0
B.x-y-z+3/2=0
C.x-y+z-3/2=0
D.x-y+z+3/2=0答案:A解析:提示:F(x,y,z)=x2+y2+z-1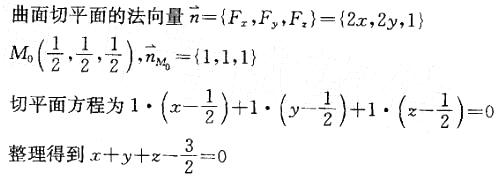
-
第3题:
曲面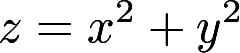 与平面
与平面  平行的切平面的方程是答案:解析:
平行的切平面的方程是答案:解析:
-
第4题:
设直线L过A(1,0,0),B(0,1,1)两点,将L绕z轴旋转一周得到曲面∑,∑与平面z=0,z=2所围成的立体为Ω.
(Ⅰ)求曲面∑的方程;
(Ⅱ)求Ω的形心坐标.答案:解析:【分析】利用定义求旋转曲面∑的方程;利用三重积分求Ω的形心坐标.
-
第5题:
求曲面x2+2y2+3z2=21的切平面,使它平行于平面x+4y+6z=0。答案:解析:
-
第6题:
过点Mo(1,-1,0)且与平面x-y+3z=1平行的平面方程为_______.答案:解析:由于已知平面的法线向量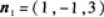 所求平面与已知平面平行,可取所求平面法线向量
所求平面与已知平面平行,可取所求平面法线向量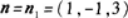 又平面过点Mo(1,-1,0),由平面的点法式方程可知,所求平面为
又平面过点Mo(1,-1,0),由平面的点法式方程可知,所求平面为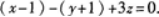
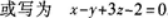 【评析】上述两种形式都正确.前者为平面的点法式方程;后者为平面的一般式方程.
【评析】上述两种形式都正确.前者为平面的点法式方程;后者为平面的一般式方程. -
第7题:
曲面xyz=1上平行于x+y+z+3=0的切平面方程是:()
- A、x+y+z=0
- B、x+y+z=1
- C、x+y+z=2
- D、x+y+z=3
正确答案:D -
第8题:
在空间直角坐标系中,方程x=2表示().
- A、x轴上的点(2,0,0)
- B、xOy平面上的直线x=2
- C、过点(2,0,0)且平行于yOz面的平面
- D、过点(2,0,0)的任意平面
正确答案:C -
第9题:
单选题下列平面中,平行于且非重合与 坐标面yoz的平面方程是()。Ay+z+1=0
Bz+1=0
Cy+1=0
Dx+1=0
正确答案: C解析: -
第10题:
单选题曲面xyz=1上平行于x+y+z+3=0的切平面方程是:()Ax+y+z=0
Bx+y+z=1
Cx+y+z=2
Dx+y+z=3
正确答案: B解析: 暂无解析 -
第11题:
填空题曲面z-ez+2xy=3在点(1,2,0)处的切平面方程为____。正确答案: 4(x-1)+2(y-2)=0解析:
构造函数F(x,y,z)=z-ez+2xy-3,则Fx′=2y,Fy′=2x,Fz′=1-ez。故将点(1,2,0)代入上式,即可得此点处切平面的法线向量为n=(4,2,0),则切平面方程为4(x-1)+2(y-2)=0。 -
第12题:
填空题曲面z=x2+y2与平面2x+4y-z=0平行的切平面的方程是____。正确答案: 2x+4y-z-5=0解析:
设曲面上有点P0(x0,y0,z0),使得曲面在此点的切平面与平面2x+4y-z=0平行,由曲面方程z=x2+y2得,曲面在P0处的法向量为(-2x0,-2y0,1),它应该与已知平面2x+4y-z=0的法向量n=(2,4,-1)平行,即-2x0/2=-2y0/4=1/(-1),解得x0=1,y0=2,z0=x02+y02=5,故所求切平面方程为2(x-1)+4(y-2)-(z-5)=0,即2x+4y-z-5=0。 -
第13题:
方程 表示下述哪种曲面?
表示下述哪种曲面?
A.单叶双曲面 B.双曲柱面
C.双曲柱面在平面x=0上投影 D.x=-3平面上双曲线答案:D解析:提示:两曲面联立表示空间一曲线,进一步可断定为在x=-3平面上的双曲线。 -
第14题:
求曲面 的平行于平面
的平行于平面 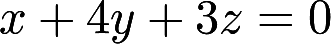 的切平面方程答案:解析:
的切平面方程答案:解析:
-
第15题:
曲面x^2+cos(xy)+yz+x=0在点(0,1,-1)处的切平面方程为A.Ax-y+z=-2
B.x+y+z=0
C.x-2y+z=-3
D.x-y-z=0答案:A解析: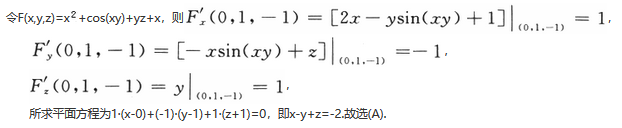
-
第16题:
曲面z=x(1-siny)+y^2(1-sinx)在点(1,0,1)处的切平面方程为________.答案:1、2x-y-z=1.解析:
-
第17题:
试求通过点Mo(一1,0,4),垂直于平面Ⅱ:3x一4y-10=0,且与直线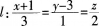 平行的平面方程。 答案:解析:平面Ⅱ的法向量m=(3-4,1),直线Z的方向向量l=(3,l,2),所以所求平面的法向
平行的平面方程。 答案:解析:平面Ⅱ的法向量m=(3-4,1),直线Z的方向向量l=(3,l,2),所以所求平面的法向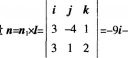
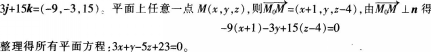
-
第18题:
过坐标原点且与平面2x-y+z+1=0平行的平面方程为______.答案:解析:已知平面的法线向量n1=(2,-1,1),所求平面与已知平面平行,可设所求平面方程为2x-y+z+D=0,将x=0,y=0,z=0代入上式,可得D=0,因此所求平面方程为2x-y+z=0. -
第19题:
已知曲面z=4-x2-y2上点P处的切平面平行于平面2x+2y+z-1=0,则点P的坐标是().
- A、(1,-1,2)
- B、(1,1,2)
- C、(-1,1,2)
- D、(-1,-1,2)
正确答案:B -
第20题:
单选题设平面α平行于两直线x/2=y/(-2)=z及2x=y=z,且与曲面z=x2+y2+1相切,则α的方程为( )。A4x+2y-z=0
B4x-2y+z+3=0
C16x+8y-16z+11=0
D16x-8y+8z-1=0
正确答案: B解析:
由平面α平行于两已知直线可得,平面α的法向量为:n=(2,-2,1)×(1,2,2)=-3(2,1,-2)。设切点为(x0,y0,z0),则切点处曲面的法向量为(2x0,2y0,-1),故2/(2x0)=1/(2y0)=(-2)/(-1),由此解得x0=1/2,y0=1/4,从而z0=x02+y02+1=21/16,因此α的方程为:2(x-1/2)+(y-1/4)-2(z-21/16)=0,即16x+8y-16z+11=0。 -
第21题:
单选题在空间直角坐标系中,方程x=2表示().Ax轴上的点(2,0,0)
BxOy平面上的直线x=2
C过点(2,0,0)且平行于yOz面的平面
D过点(2,0,0)的任意平面
正确答案: B解析: 暂无解析 -
第22题:
单选题下列平面中,平行于且与yOz坐标面非重合的平面方程是( )。[2018年真题]Ay+z+1=0
Bz+1=0
Cy+1=0
Dx+1=0
正确答案: D解析:
D项,平面方程x+1=0化简为x=-1,显然平行yOz坐标面,且不重合。ABC三项,均不平行于yOz坐标面。 -
第23题:
单选题已知曲面z=4-x2-y2上点P处的切平面平行于平面π:2x+2y+z-1=0,则点P的坐标是( )。A(1,-1,2)
B(-1,1,2)
C(1,1,2)
D(-1,-1,2)
正确答案: D解析:
即求曲面S:F(x,y,z)=0,其中F(x,y,z)=z+x2+y2-4上点P使S在该点处的法向量n与平面π:2x+2y+z-1=0的法向量n0=(2,2,1)平行。S在P(x,y,z)处的法向量n=(∂F/∂x,∂F/∂y,∂F/∂z)=(2x,2y,1)
n∥n0⇔n=λn0
λ为常数,即2x=2λ,2y=2λ,1=λ。即x=1,y=1,又点P(x,y,z)∈S⇒z=4-x2-y2|(x,y)=(1,1)=2,求得P(1,1,2)(P不在给定的平面上)。 -
第24题:
单选题曲面z=x2+y2与平面2x+4y-z=0平行的切平面的方程是( )。A2x+4y-z-5=0
B2x+4y-z=0
C2x+4y-z-3=0
D2x+4y-z+5=0
正确答案: B解析:
设曲面上有点P0(x0,y0,z0),使得曲面在此点的切平面与平面2x+4y-z=0平行,由曲面方程z=x2+y2得,曲面在P0处的法向量为(-2x0,-2y0,1),它应该与已知平面2x+4y-z=0的法向量n=(2,4,-1)平行,即-2x0/2=-2y0/4=1/(-1),解得x0=1,y0=2,z0=x02+y02=5,故所求切平面方程为2(x-1)+4(y-2)-(z-5)=0,即2x+4y-z-5=0。
