设函数f（x）在点x=a处可导，则函数｜f（x）｜在点x=a处不可导的充分条件是（ ）A.f（a）=0且f′（a）=0 B.f（a）=0且f′（a）≠0 C.f（a）＞0且f′（a）＞ D.f（a）＜0且f′（a）＜

题目
设函数f（x）在点x=a处可导，则函数｜f（x）｜在点x=a处不可导的充分条件是（ ）

A.f（a）=0且f′（a）=0
B.f（a）=0且f′（a）≠0
C.f（a）＞0且f′（a）＞
D.f（a）＜0且f′（a）＜
相似考题

1.以下结论正确的是()。A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.

2.若f(x)在处可导,则∣f(x)∣在x=x0处()A、可导B、不可导C、连续但未必可导D、不连续

3.若f（x）在点x=a处可导，则f′（a）≠（ ）。

4.设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。A、0B、π/2C、锐角D、钝角

更多“设函数f（x）在点x=a处可导，则函数｜f（x）｜在点x=a处不可导的充分条件是（ ）”相关问题

  • 第1题：

    已知函数f(x)在x=1处可导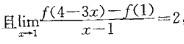，则f'(1)等于：
    A. 2 B. 1


    答案：D
    解析：
    解：可利用函数在一点x0可导的定义，通过计算得到最后结果。
    选D。

  • 第2题：

    设函数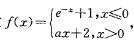若f(x)在x=0处可导，则a的值是：
    A. 1 B. 2 C. 0 D. -1


    答案：D
    解析：
    提示:已知f(x)在x=0处可导，要满足f'+ (0) =f'- (0)。

    得 a= -1

  • 第3题：

    设函数z=f(xy，yg(x))，其中函数f具有二阶连续偏导数，函数g(x)可导且在x=1处取得极值g(1)=1.求


    答案：
    解析：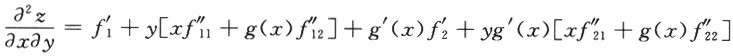

    所以，令x=y=1，且注意到g(1)=1，g'(1)=0，得

  • 第4题：

    (Ⅰ)证明拉格朗日中值定理：若函数f(x)在［a，b］上连续，在(a，b)内可导，则存在ξ∈(a，b)，使得f(b)-f(a)=f'(ξ)(b-a)；(Ⅱ)证明：若函数f(x)在x=0处连续，在(0，δ)(δ>0)内可导，且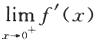=A，则存在，且.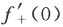


    答案：
    解析：

  • 第5题：

    下列命题中，正确的是( ).

    A.单调函数的导函数必定为单调函数
    B.设f´(x)为单调函数，则f(x)也为单调函数
    C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点
    D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0

    答案：D
    解析：
    可导函数的极值点必定是函数的驻点，故选D.

  • 第6题：

    设其中g(x)是有界函数，则f(x)在x=0点( )。

    A、极限不存在
    B、极限存在但不连续
    C、连续、但不可导
    D、可导

    答案：D
    解析：

  • 第7题：

    设y=f(x)可导，点a0=2为f(x)的极小值点，且f(2)=3，则曲线y=f(x)在点(2，3)处的切线方程为______．


    答案：
    解析：
    由于y=f(x)可导，点x0=2为f(x)的极小值点，由极值的必要条件可知f′(2)=0．曲线y=fx)在点(2，3)处的切线方程为y-3=f′(2)(x-2)=0，即y=3为所求切线方程．

  • 第8题：

    下列结论不正确的是（）。

    • A、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处连续
    • B、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处可导
    • C、z=f（x，y）在点（x0，y0）处可导，则f（x，y）在点（x0，y0）处可微
    • D、z=f（x，y）在点（x0，y0）处偏导数连续，则f（x，y）在点（x0，y0）处连续

    正确答案:C

  • 第9题：

    设函数f(x)=丨x丨，则函数在点x=0处（）

    • A、连续且可导
    • B、连续且可微
    • C、连续不可导
    • D、不可连续不可微

    正确答案:C

  • 第10题：

    单选题
    设函数f(x)=丨x丨，则函数在点x=0处（）
    A

    连续且可导

    B

    连续且可微

    C

    连续不可导

    D

    不可连续不可微


    正确答案： C
    解析： 暂无解析

  • 第11题：

    判断题
    若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第12题：

    单选题
    函数f（x）在点x＝x0处连续是f（x）在点x＝x0处可微的（　　）。[2019年真题]
    A

    充分条件

    B

    充要条件

    C

    必要条件

    D

    无关条件


    正确答案： A
    解析：
    可导等价于可微，可导必连续，而连续未必可导，如函数y＝|x|在x＝0处函数连续但不可导。因此可微是连续的充分条件，连续是可微的必要条件。

  • 第13题：

    函数f（x）在点x＝x0处连续是f（x）在点x＝x0处可微的（　　）。

    A．充分条件
    B．充要条件
    C．必要条件
    D．无关条件

    答案：C
    解析：
    可导等价于可微，可导必连续，而连续未必可导，如函数y＝|x|在x＝0处函数连续但不可导。因此可微是连续的充分条件，连续是可微的必要条件。

  • 第14题：

    下列命题正确的是（）

    A.函数f(x)的导数不存在的点，一定不是f(x)的极值点
    B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点
    C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)＝0
    D.若函数f(x)在点x0处连续，则f'(x0)一定存在

    答案：C
    解析：
    根据函数在点x0处取极值的必要条件的定理，可知选项C是正确的．

  • 第15题：

    设函数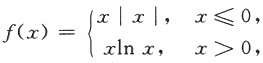则x=0是f(x)的

    A.A可导点，极值点B
    B.不可导点，极值点
    C.可导点，非极值点
    D.不可导点，非极值点

    答案：B
    解析：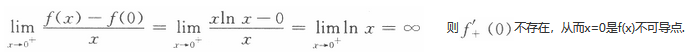

    又在x=0的左半邻域f(x)=x｜x｜<0=f(0)，
    　　在x=0的右半邻域f(x)=xln x<0=f(0)，
    　　则f(x)在x=0处取极大值，故应选(B).

  • 第16题：

    已知函数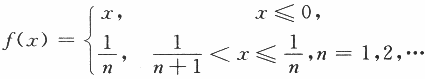，则



    A.Ax=0是f(x)的第一类间断点
    B.x=0是f(x)的第二类间断点
    C.f(x)在x=0处连续但不可导
    D.f(x)在x=0处可导

    答案：D
    解析：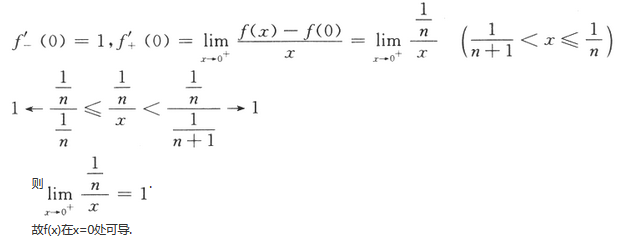

  • 第17题：

    设f(x)在x=a的某个邻域内有定义，则f(x)在x-a处可导的一个充分条件是( )。



    答案：D
    解析：
    用可导的定义判断

  • 第18题：

    函数f(x)在点x=x0处连续是f(x)在x0处可导的（　　）

    A.充分非必要条件
    B.必要非充分条件
    C.充分必要条件
    D.既非充分条件也非必要条件

    答案：B
    解析：
    由可导与连续的关系：“可导必定连续，连续不一定可导”可知，应选B．

  • 第19题：

    若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.


    正确答案:错误

  • 第20题：

    以下叙述正确的是：连续函数f（x）在[a，b]上的定积分等于（）。

    • A、f（x）的导函数在b点的值减去在a点的值
    • B、f（x）的导函数在a点的值减去在b点的值
    • C、f（x）的原函数在b点的值减去在a点的值
    • D、f（x）的原函数在a点的值减去在b点的值

    正确答案:C

  • 第21题：

    下列结论不正确的是（）。

    • A、y=f（x）在点x0处可微，则f（x）在点x0处连续
    • B、y=f（x）在点x0处可微，则f（x）在点x0处可导
    • C、y=f（x）在点x0处连续，则f（x）在点x0处可微
    • D、y=f（x）在点x0处可导，则f（x）在点x0处连续

    正确答案:C

  • 第22题：

    单选题
    若f（x）在x0点可导，则|f（x）|在点x0点处（　　）。
    A

    必可导

    B

    连续但不一定可导

    C

    一定不可导

    D

    不连续


    正确答案： C
    解析：
    f（x）在x＝0处可导，则必在x＝0处连续，故|f（x）|在x＝0处必连续，排除D项；
    设f（x）＝x，f（x）在x＝0处可导，但|f（x）|＝|x|在x＝0处不可导，排除A项；
    设f（x）＝x2，则f（x）和|f（x）|在x＝0处都可导，排除C项。

  • 第23题：

    单选题
    下列说法中正确的是（　　）。[2014年真题]
    A

    若f′（x0）=0，则f（x0）必须是f（x）的极值

    B

    若f（x0）是f（x）的极值，则f（x）在点x0处可导，且f′（x0）=0

    C

    若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的必要条件

    D

    若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的充分条件


    正确答案： B
    解析：
    当f（x0）在点x0处可导时，若f（x）在x0处取得极值，则可知f′（x0）=0；若f′（x0）＝0，f（x）在点x0未必取得极值，例如f（x）＝x3在点x＝0处有f′（0）＝0，但x3在实数域内不存在极值点。

相关内容