若D是由x轴、y轴及直线2x+y-2=0所围成的闭区域,则二重积分的值等于( )A.1 B.2 C.1/2 D.-1
题目
若D是由x轴、y轴及直线2x+y-2=0所围成的闭区域,则二重积分
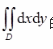
的值等于( )
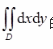
的值等于( )
A.1
B.2
C.1/2
D.-1
B.2
C.1/2
D.-1
相似考题
参考答案和解析
答案:A
解析:
原积分表示x轴、y轴及直线2x+y-2=0所围成的闭区域的面积,因此


更多“若D是由x轴、y轴及直线2x+y-2=0所围成的闭区域,则二重积分 ”相关问题
-
第1题:
Ω是由曲面z=x2+y2,y=x,y=0,z=1在第一卦限所围成的闭区域,f(x,y,z) 在Ω上连续,则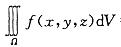 等于:
等于:
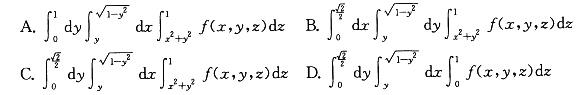 答案:C解析:提示:作出Ω的立体图形,并确定Ω在xOy平面上投影区域:Dxy:x2+y2 = 1,写出在直角坐标系下先z后x最后y的三次积分。
答案:C解析:提示:作出Ω的立体图形,并确定Ω在xOy平面上投影区域:Dxy:x2+y2 = 1,写出在直角坐标系下先z后x最后y的三次积分。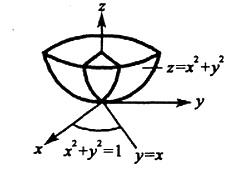
-
第2题:
已知D为x轴、y轴和抛物线y=1-x2所围成的在第一象限内的闭区域,则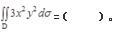
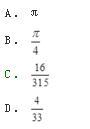 答案:C解析:积分区域D形状如图所示。
答案:C解析:积分区域D形状如图所示。
计算得抛物线与x轴、y轴的交点分别为(1,0)、(0,1),从而D={(x,y)|0≤y≤1-x2,x∈[0,1]},则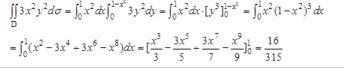
-
第3题:
D域由x轴、x2+y2-2x=0(y≥0)及x+y=2 所围成,f(x,y)是连续函 答案:B解析:提示:x2+y2-2x=0,(x-1)2+y2 =1,D由(x-1)2+y2 =1,(y≥0),x+y =2围成,画出
答案:B解析:提示:x2+y2-2x=0,(x-1)2+y2 =1,D由(x-1)2+y2 =1,(y≥0),x+y =2围成,画出
-
第4题:
由曲线y=x3,直线x=1,z轴围成的平面有界区域的面积为_________.答案:解析:【答案】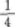
【考情点拨】本题考查了积分的应用的知识点.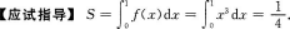
-
第5题:
计算二重积分 ,其中积分区域D是由x=0、x=1、y=0、y=1所围成的闭区域答案:解析:
,其中积分区域D是由x=0、x=1、y=0、y=1所围成的闭区域答案:解析:







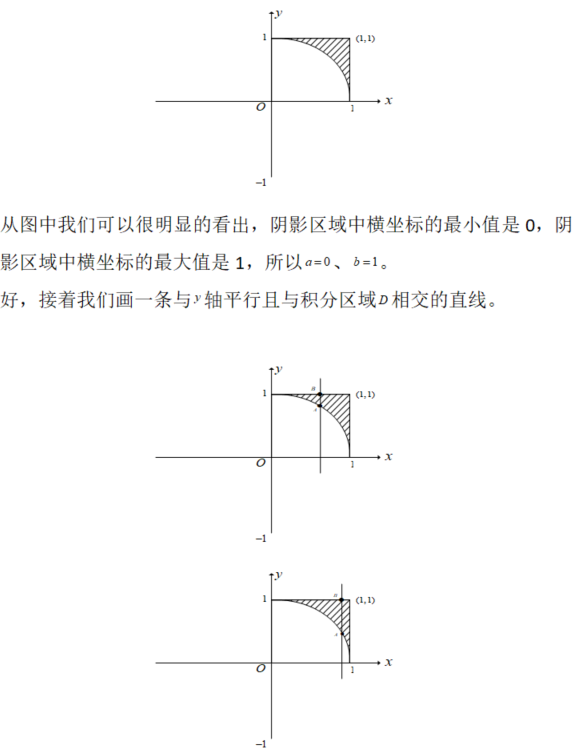



-
第6题:
请计算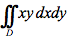 ,其中D是由y=1/x=2,y=x所围成的闭区域答案:解析:
,其中D是由y=1/x=2,y=x所围成的闭区域答案:解析:


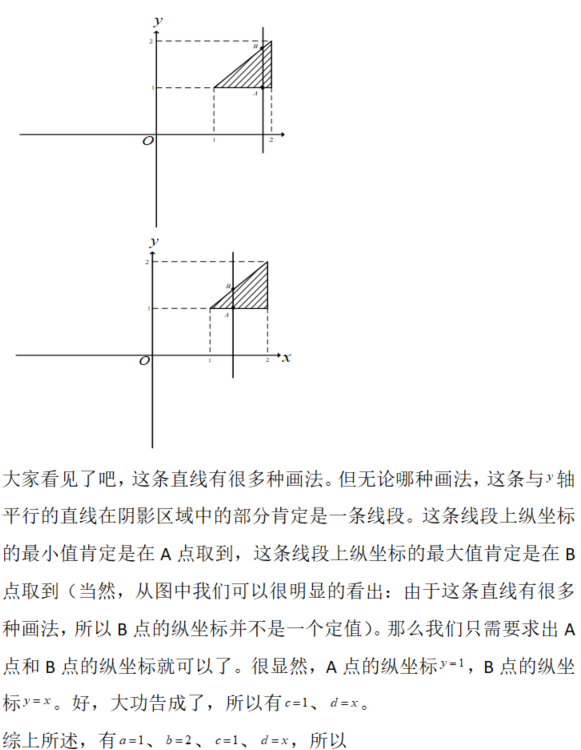



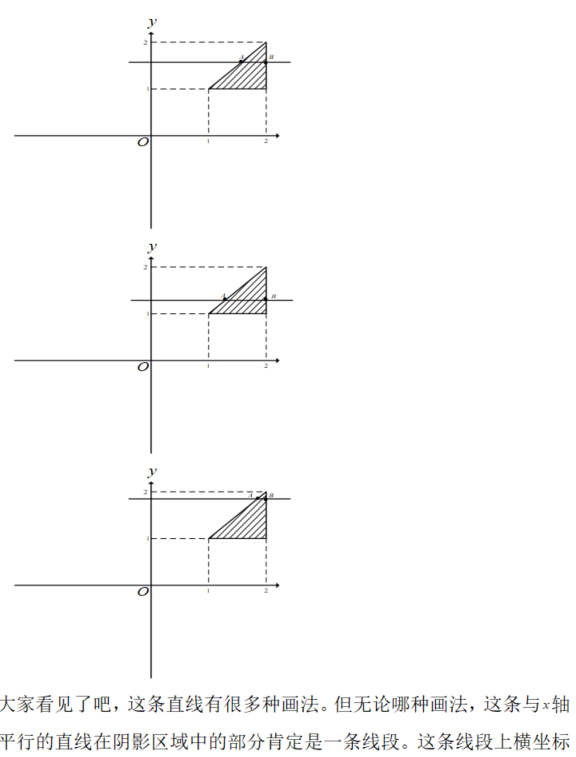


-
第7题:
设非负函数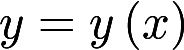 满足微分方程
满足微分方程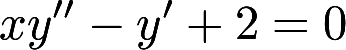 ,当曲线
,当曲线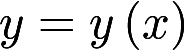 过原点时,其与直线x=1及y=0围成平面区域D的面积为2,求D绕y轴旋转所得旋转体的体积答案:解析:
过原点时,其与直线x=1及y=0围成平面区域D的面积为2,求D绕y轴旋转所得旋转体的体积答案:解析:
-
第8题:
过点(0,1)点作曲线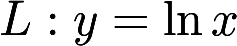 的切线,切点为A,又L与x轴交于B点,区域D由与L直线AB及x轴围成,求区域D的面积及D绕x轴旋转一周所得旋转体的体积.答案:解析:
的切线,切点为A,又L与x轴交于B点,区域D由与L直线AB及x轴围成,求区域D的面积及D绕x轴旋转一周所得旋转体的体积.答案:解析: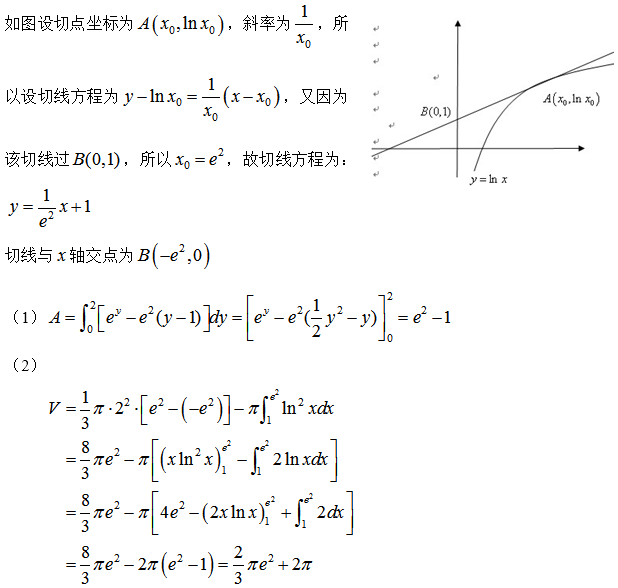
-
第9题:
曲线y=sinx(0≤x≤π/2)与直线x=π/2,y=0围成的平面图形绕x轴旋转产生的旋转体体积是()。 答案:A解析:提示:利用旋转体体积公式
答案:A解析:提示:利用旋转体体积公式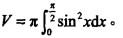
-
第10题:
设区域D是由直线y=x,x=2,y=1围成的封闭平面图形,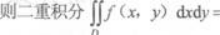
 答案:D解析:积分区域如右图中阴影部分所示.D可以表示为1≤x≤2,1≤y≤x或1≤y≤2,y≤x≤2.对照所给选项,知应选D.
答案:D解析:积分区域如右图中阴影部分所示.D可以表示为1≤x≤2,1≤y≤x或1≤y≤2,y≤x≤2.对照所给选项,知应选D.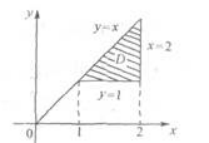
-
第11题:
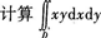 ,其中区域如图5-3所示,由y=x,y=1与Y轴围成.答案:解析:将所给积分化为二次积分.
,其中区域如图5-3所示,由y=x,y=1与Y轴围成.答案:解析:将所给积分化为二次积分.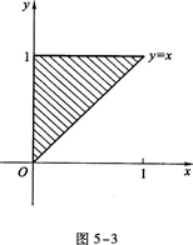
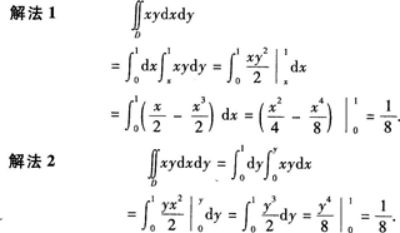
-
第12题:
计算二重积分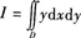
,其中D是由直线
及y=1围
成的平面区域.答案:解析:所给积分区域D如图5-6所示,如果选择先对y积分后对x积分的二次积分,需要将积分区域划分为几个子区域,如果选择先对x积分后对y积分的二次积分,区域D可以表示为
0≤y≤1,Y≤x≤y+1,
因此
【评析】
上述分析通常又是选择积分次序问题的常见方法.

-
第13题:
若D是由x=0,y=0,x2+y2=1所围成在第一象限的区域,则二重积分
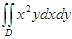
等于( )。
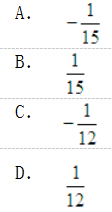 答案:B解析:采用极坐标法求二重积分,具体计算如下:
答案:B解析:采用极坐标法求二重积分,具体计算如下:
-
第14题:
D 域由 x 轴,x2 + y2 ? 2x = 0( y ≥ 0)及 x+y=2 所围成, f (x, y)是连续函数,化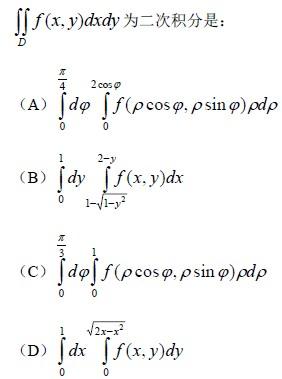 答案:B解析:解:选 B。
答案:B解析:解:选 B。
画积分区域如下图所示,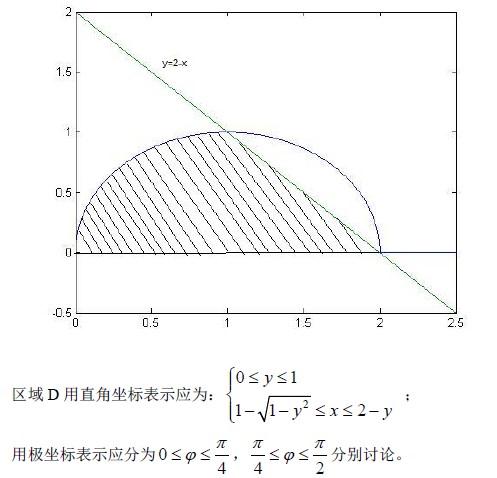
-
第15题:
设D为曲线y=1-x2,直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)·
①求平面图形的面积;
②求平面图形D绕x轴旋转一周所成旋转体的体积Vx.答案:解析: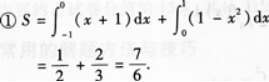
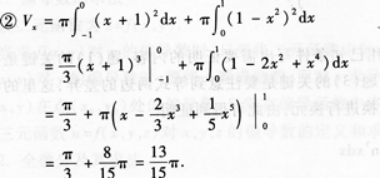
-
第16题:
设D是由直线y=1,y=x,y=-x围成的有界区域,计算二重积分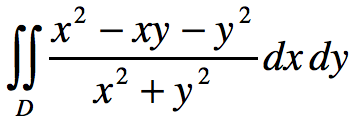 答案:解析:
答案:解析: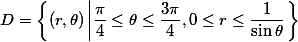
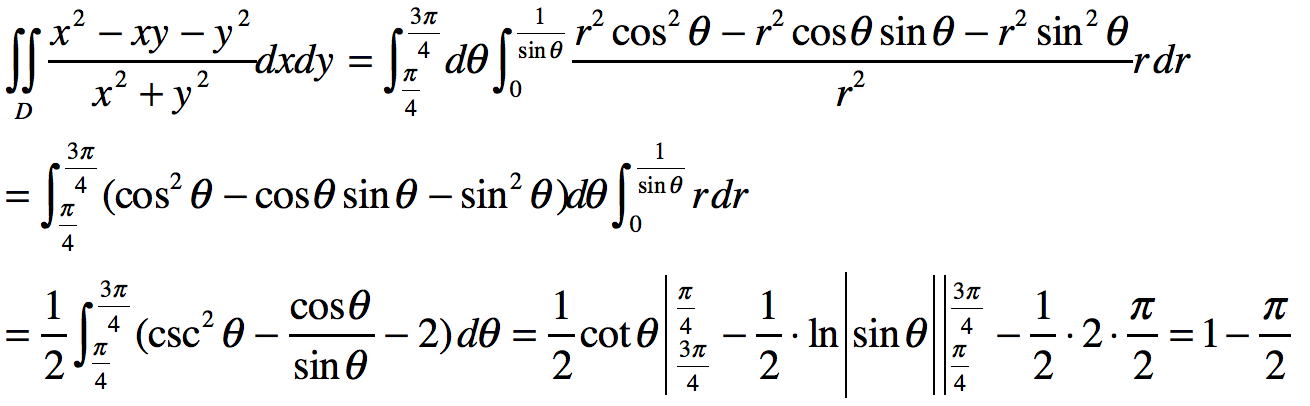
-
第17题:
设f(x,y)为连续函数,且满足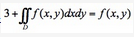 ,其中D是由x轴、y轴、
,其中D是由x轴、y轴、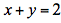 所围成的闭区域答案:解析:
所围成的闭区域答案:解析:

-
第18题:
请计算二重积分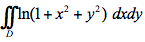 ,其中D是由圆周
,其中D是由圆周 、x轴,y轴所围成的在第一象限内的闭区域答案:解析:
、x轴,y轴所围成的在第一象限内的闭区域答案:解析:



-
第19题:
设D是两个坐标轴和直线x+y=1所围成的三角形区域,则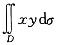 的值为:
的值为:
 答案:C解析:提示:画出积分区域D的图形,把二重积分化为二次积分,
答案:C解析:提示:画出积分区域D的图形,把二重积分化为二次积分,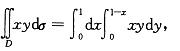 ,计算出最后答案。
,计算出最后答案。 -
第20题:
D域由x轴、x2+y2-2x=0(y≥0)及x+y=2 所围成,f(x,y)是连续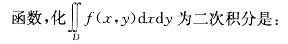
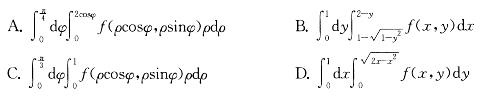 答案:B解析:提示 x2+y2-2x=0,(x-1)2+y2 =1,D由(x-1)2+y2 =1,(y≥0),x+y =2与x
答案:B解析:提示 x2+y2-2x=0,(x-1)2+y2 =1,D由(x-1)2+y2 =1,(y≥0),x+y =2与x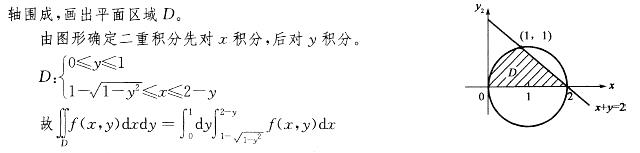
-
第21题:
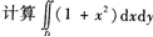
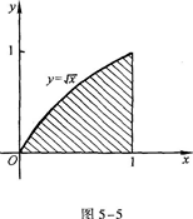
,其中D是由
及x轴所围成的平面区域.答案:解析:积分区域D如图5-5所示.若选择先对Y积分后对x积分,区域D可以表示为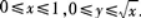
因此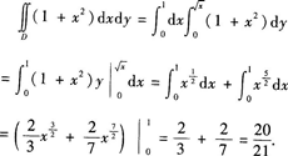
-
第22题:
求由曲线y2=(x-1)3和直线x=2所围成的图形绕x轴旋转所得的旋转体的体积.?答案:解析:
-
第23题:
求由曲线y=x2(x≥0),直线y=1及Y轴围成的平面图形的面积·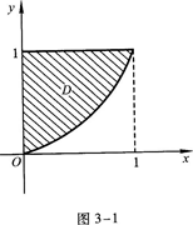 答案:解析:y=x2(x≥0),y=1及y轴围成的平面图形D如图3—1所示.其面积为
答案:解析:y=x2(x≥0),y=1及y轴围成的平面图形D如图3—1所示.其面积为
