设X1,X2,…,Xn是来自总体X的样本,,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
题目
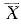 ,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。
相似考题
参考答案和解析
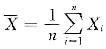 ,经计算
,经计算 从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立
从而(B)正确而(A)不正确,而(C)、(D)需要总体X服从正态分布N(μ,σ2)才能成立更多“设X1,X2,…,Xn是来自总体X的样本,,s2分别是样本均值和样本方差,E(X)=μ,D(X)=σ2,则有( )。”相关问题
-
第1题:
设X1,X2,…,Xn是来自正态总体N(μ,σ2)的一个样本,
 与s分别为其观测值的样本均值与样本标准差,则在下列抽样分布中正确表述的有( )。
与s分别为其观测值的样本均值与样本标准差,则在下列抽样分布中正确表述的有( )。 正确答案:AD
正确答案:AD
解析:设X1,X2,…,Xn是来自正态总体N(μ,σ2)一个样本,则,对样本均值施行标准化变换,则有:。当用样本标准差s代替中的σ时,有。 -
第2题:
设X1,X2,…,Xn是来自正态总体N(μ,σ2)的一个样本,则有( )。
 正确答案:AC
正确答案:AC
解析:正态均值μ的无偏估计有两个,一个是样本均值,即:,另一个是样本中位数;即:正态方差σ2的无偏估计常用的只有一个,就是样本方差s2,即 -
第3题:
设X1,X2,…,Xn是简单随机样本,则有( )。
A.X1,X2,…,Xn相互独立
B.X1,X2,…,Xn有相同分布
C.X1,X2,…,Xn彼此相等
D.X1与(X1+X2)/2同分布
E.X1与Xn的均值相等
正确答案:ABE
解析:简单随机样本满足随机性和独立性,且每一个样本都与总体同分布,样本均值相等。 -
第4题:
设总体X~N(μ,σ^2),X1,X2,…,Xn为总体X的简单随机样本,X与S^2分别为样本均值与样本方差,则(). 答案:A解析:
答案:A解析:
-
第5题:
设总体X的概率密度为
未知参数,X1,X2, ...Xn是来自总体X的样本,则θ的矩估计量是: 答案:B解析:
答案:B解析: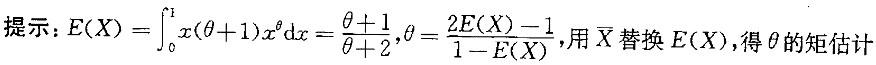

-
第6题:
设X1,X2,…Xn是简单随机样本,则有( )。
A. X1,X2,…Xn相互独立 B. X1,X2,…Xn有相同分布
C. X1,X2,…Xn彼此相等 D.X1与(X1,+X2)/2同分布
E.X1与Xn的均值相等答案:A,B,E解析:简单随机样本满足随机性和独立性,且每一个样本都与总体同分布,样本均值相等。 -
第7题:
设总体X~U(θ,θ),X1,X2,…,Xn是来自总体X的样本,求θ1,θ2的矩估计和最大似然估计.答案:解析:
-
第8题:
设x为总体,E(X)=μ,D(x)=σ^2,X1,X2,…,xn为来自总体的简单随机样本,S^2=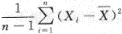 ,则E(S^2)=_______.答案:解析:
,则E(S^2)=_______.答案:解析: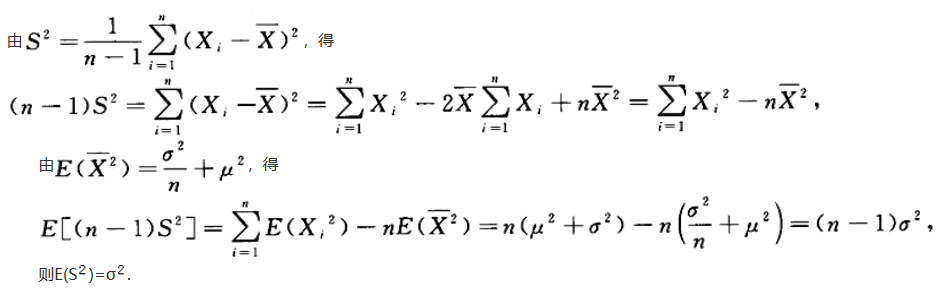
-
第9题:
设总体X~N(μ,σ^2),X1,X2,…,xn为总体的简单样本,S^2为样本方差,则D(S^2)=_______.答案:解析: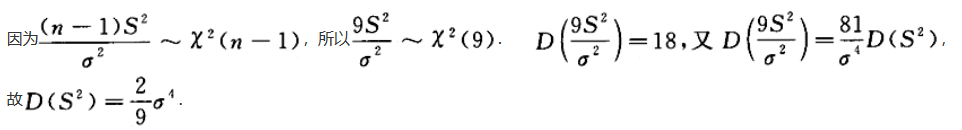
-
第10题:
设总体X~N(0,σ2),X1,X2,...Xn是自总体的样本,则σ2的矩估计是: 答案:D解析:提示 注意 E(x)=0,σ2=D(x)=E(x2) - [E(x)]2=E(x2),σ2也是x的二阶原点矩,σ2的矩估计量是样本的二阶原点矩。
答案:D解析:提示 注意 E(x)=0,σ2=D(x)=E(x2) - [E(x)]2=E(x2),σ2也是x的二阶原点矩,σ2的矩估计量是样本的二阶原点矩。 -
第11题:
设样本x1,x2,…,xn来自正态总体N(0,9),其样本方差为s2,则E(s2)=()
正确答案:9 -
第12题:
问答题设总体X~N(μ,σ2),x1,x2,…xn为其样本,为样本均值,则____.正确答案:解析: -
第13题:
设总体X~N(2,42),(x1,x2,…,Xn)是来自X的简单随机样本,则下面结果正确的是( )。

A.
B.
C.
D.
正确答案:D
解析:如果X~N(μ,σ2),(X1,X2,…,Xn)是来自X的简单随机样本,则。X~N(2,42),则,标准化后,~N(0,1)。 -
第14题:
设X1,X2,…,Xn是一个样本,样本的观测值分别为x1,x2,…,xn,则样本方差s2的计算公式正确的有( )。
 正确答案:ACD
正确答案:ACD
解析: -
第15题:
设(X1,X2,…,Xn)(N≥2)为标准正态总体X的简单随机样本,则().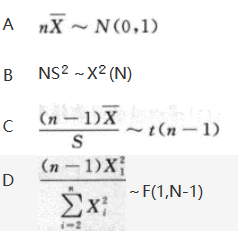 答案:D解析:
答案:D解析: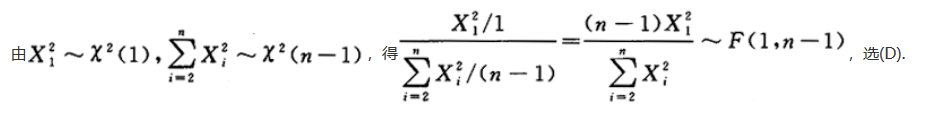
-
第16题:
设X1,X2,…,Xn是来自正态总体N(μ,σ2)的一个样本,,s2分别是样本均值和样本方差,令,则有( )。A、W~t(n)
B、W~t(n-1)
C、W~F(n)
D、W~F(n-1)答案:B解析:由常用的统计量的分布知W~t(n-1) -
第17题:
设总体X的概率密度为f(x)=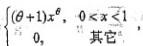 其中θ>-1是未知参数,X1,X2,...Xn是来自总体X的样本,则θ的矩估计量是:
其中θ>-1是未知参数,X1,X2,...Xn是来自总体X的样本,则θ的矩估计量是:
 答案:B解析:X的数学期望
答案:B解析:X的数学期望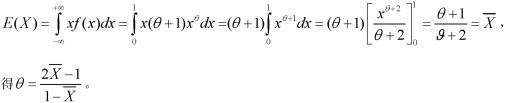
-
第18题:
设总体X~N(μ,25),X1,X2,…,X100为来自总体的简单随机样本,求样本均值与总体均值之差不超过1.5的概率答案:解析: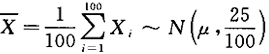 总体均值为E(X)=μ,
总体均值为E(X)=μ,
则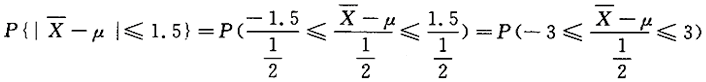
=Ф(3)-Ф(-3)=2Ф(3)-1=0.9973 -
第19题:
设总体X的密度函数为f(x)= ,(X1,X2,…,Xn)为来自总体X的简单随机样本.(1)求θ的矩估计量θ;(2)求D(θ).答案:解析:
,(X1,X2,…,Xn)为来自总体X的简单随机样本.(1)求θ的矩估计量θ;(2)求D(θ).答案:解析:
-
第20题:
设总体X服从正态分布N(μ,σ^2)(σ>0),从该总体中抽取简单随机样本X1,X2,…,Xn(n≥2),其样本均值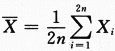 ,求统计量
,求统计量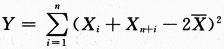 的数学期望E(Y).答案:解析:
的数学期望E(Y).答案:解析: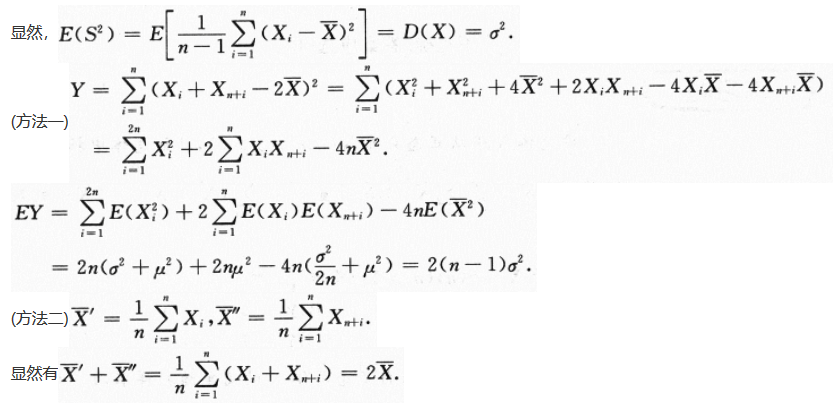
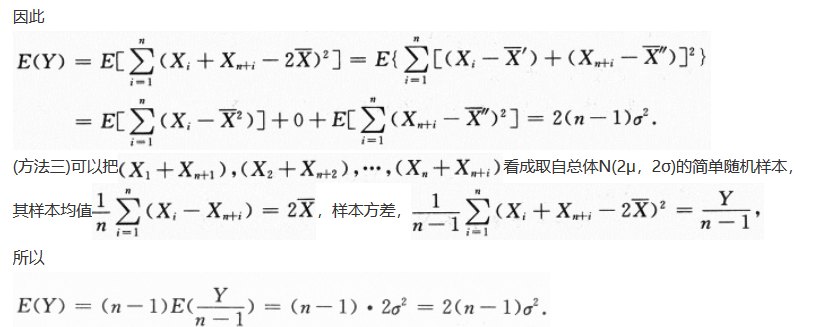
-
第21题:
设总体X的均值μ及方差σ2都存在,且有σ2>0,但μ,σ2均未知,又设X1,X2,…,Xn是来自总体x的样本,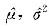 是μ,σ2的矩估计量,则有( )。
是μ,σ2的矩估计量,则有( )。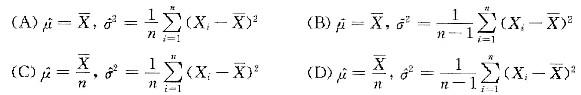 答案:A解析:由矩估计法有
答案:A解析:由矩估计法有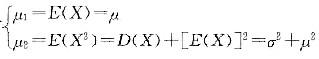 解得
解得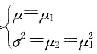 ,因此有
,因此有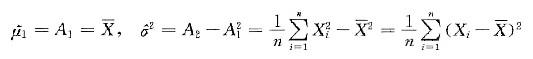
-
第22题:
设有两个样本,样本A:x1, X2 ,…,Xn ;样本B:x1+d,x2+d,x···,xn+d(d为常数)又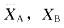 分别为它们的样本均值,S2A,S2B分别为它们的样本方差,则 ( )。
分别为它们的样本均值,S2A,S2B分别为它们的样本方差,则 ( )。
 答案:C,D解析:
答案:C,D解析: -
第23题:
设X1,X2,…,Xn是从总体X中抽取的容量为n的一个样本,如果由此样本构造一个函数T(X1,X2,…,Xn),不依赖于任何未知参数,则函数T(X1,X2,…,Xn)是一个()
正确答案:统计量
