—平面简谐波沿x轴正方向传播，振幅A=0. 02m，周期T=0. 5s，波长λ=100m，原点处质元的初相位φ=0，则波动方程的表达式为： A.y=0.02cos2π(t/2-0.01x) (SI) B.y=0.02cos2π(2t-0.01x) (SI) C.y=0.02cos2π(t/2-100x) (SI) D.y=0.02cos2π(2t-100x) (SI)
题目
B.y=0.02cos2π(2t-0.01x) (SI)
C.y=0.02cos2π(t/2-100x) (SI)
D.y=0.02cos2π(2t-100x) (SI)
相似考题
参考答案和解析
更多“—平面简谐波沿x轴正方向传播，振幅A=0. 02m，周期T=0. 5s，波长λ=100m，原点处质元的初相位φ=0，则波动方程的表达式为： ”相关问题
-
第1题：
一振幅为A，周期为T，波长λ的平面简谐波沿x轴负向传播，在x=λ/2处，t=T/4时，振动相位为π，则此平面简谐波的波动方程为( )。A.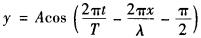
B.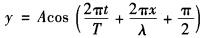
C.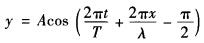
D.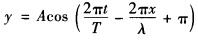
答案：C解析： -
第2题：
一平面余弦波波源的振动周期T=0.5s，所激起的波的波长λ=10m，振幅为0.5m，当t=0时，波源处振动的位移恰为正向最大值，取波源处为原点并设波沿x轴正向传播，此波的波动方程为( )。
答案：C解析：沿x轴正向传播的平面余弦波波动方程为，代入各已知数据求得φ -
第3题：
一平面简谐波沿x轴正向传播，已知波长λ，频率v，角频率w，周期T，初相Φ0，则下列表示波动方程的式子中，哪几个是正确的？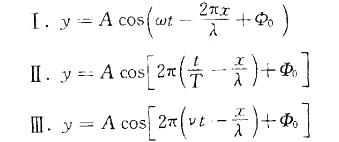
A.Ⅰ
B.Ⅰ、Ⅱ
C.Ⅱ、Ⅲ
D.Ⅰ、Ⅱ、Ⅲ答案：D解析：提示：μ=λv，w=2πv。 -
第4题：
一平面简谐波的波动方程为y=0.01cos10π(25t-x) (SI)，则在t=0. 1s时刻，x=2m处质元的振动位移是：
A. 0. 01cm B. 0. 01m
C. -0. 01m D. 0. 01mm答案：C解析： -
第5题：
—平面简谐波沿x 轴正方向传播 ，振幅A=0.02m ，周期T=0.5s ，波长λ= 100m ，原点处质元的初相位Φ=0，则波动方程的表达式为：
答案：B解析：
-
第6题：
—横波沿一根弦线传播，其方程为y=-0.02cosπ(40-50(SI) ，该波的振幅与波长分别为：A . 0. 02cm ,0.5cm
B .-0.02m ，-0.5m
C . -0. 02m ,0. 5m
D . 0. 02m ,0. 5m答案：D解析：
-
第7题：
一平面简谐波沿x轴负方向传播，其振幅A=0.01m，频率v=550Hz，波速u=330m/s。若t=0时，坐标原点处的质点达到负的最大位移，则此波的波函数为（ ）。
答案：A解析： -
第8题：
一平面简谐波以μ的速率沿x轴正向传播，角频率为ω，那么，距原点x处（x>0）质点的振动相位总是比原点处质点的振动相位（）。
- A、滞后ωx/μ
- B、滞后x/μ
- C、超前ωx/μ
- D、超前x/μ
正确答案:A -
第9题：
一平面简谐波沿x轴负方向传播，其振幅A=0.01m，频率v=550Hz，波速u=330m·s-1。若t=0时，坐标原点O处质元达到负的最大位移，则该波的表达式为（）。
- A、y=0.01cos[2π（550t+1.67x）+π]
- B、y=0.01cos[2π（550t-1.67x）+π]
- C、y=0.01cos[2π（550t+1.67x）-π]
- D、y=0.01cos[2π（550t-1.67x）-π]
正确答案:A -
第10题：
已知平面简谐波的波动方程y=0.3cos（2πt-πx）（m），则该波源的振动初相位为（），波的传播速度为（）m.s-1，波长（）m。
正确答案:0；2；2 -
第11题：
单选题一振幅为A、周期为T、波长为λ平面简谐波沿X负向传播，在X=（1／2）λ处，t=T／4时振动相位为π，则此平面简谐波的波动方程为：（）Ay=Acos（2πt／T-2πx／λ-1／2π）
By=Acos（2πt／T+2πx／λ+1／2π）
Cy=Acos（2πt／T+2πx／λ-1／2π）
Dy=Acos（2πt／T-2πx／λ+1／2π）
正确答案： A解析： 写出波动方程，X=（1／2）λ，t=T／4，φ=π代入，求初相位φ0。 -
第12题：
—横波沿一根弦线传播，其方程为=-0. 02cosπ(4x-50t)(SI) ，该波的振幅与波长分别为：A. 0. 02cm,0. 5cm
B. -0. 02m,-0. 5m
C. -0. 02m,0. 5m
D. 0. 02m,0. 5m答案：D解析：
-
第13题：
一平面谐波沿x轴正方向传播，振幅A=0.02m，周期T=0.5s，波长λ=100m，原点处质元的初相位φ=0，则波动方程的表达式为( )。A.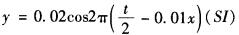
B.y=0.02cos2π(2t-0.01x)(SI)
C.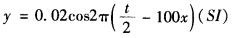
D.y=0.02cos2π(2t-100x)(SI)答案：A解析： -
第14题：
一横波沿绳子传播时的波动方程为y = 0. 05cos(4πx-10πt)(SI)，则下面关于其波长、波速的叙述，哪个是正确的？
A.波长为0. 5m B.波长为0. 05m
C.波速为25m/s D.波速为5m/s答案：A解析：提示:将波动方程化为标准形式，再比较计算。并注意到cosφ =cos(-φ)，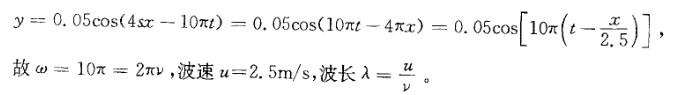
-
第15题：
一平面简谐波的波动方程为y=0.01cos10π(25t-x) (SI)，则在t=0. 1s时刻，x=2m处质元的振动位移是：A. 0. 01cm
B. 0. 01m
C. -0. 01m
D. 0. 01mm答案：C解析： -
第16题：
—平面简谐波的波动方程为y = 0. 02cos2π(10t-x/5)(SI)。t=0. 25s 时，处于平衡位置，且与坐标原点x=0最近的质元的位置是：A. ± 5 m
B. 5m
C. ±1. 25m
D. 1. 25m答案：D解析：
@## -
第17题：
一质点沿y轴方向做简谐振动，振幅为A，周期为T，平衡位置在坐标原点。在t=0时刻，质点位于y正向最大位移处，以此振动质点为波源，传播的横波波长为λ，则沿x轴正方向传播的横波方程为（ ）。
答案：C解析：
-
第18题：
一振幅为A、周期为T、波长为λ平面简谐波沿X负向传播，在X=（1／2）λ处，t=T／4时振动相位为π，则此平面简谐波的波动方程为：（）
- A、y=Acos（2πt／T-2πx／λ-1／2π）
- B、y=Acos（2πt／T+2πx／λ+1／2π）
- C、y=Acos（2πt／T+2πx／λ-1／2π）
- D、y=Acos（2πt／T-2πx／λ+1／2π）
正确答案:C -
第19题：
一平面简谐波沿x轴正向传播，已知波长λ，频率υ，角频率ω，周期T，初相Ф0，则下列表示波动方程的式子中，哪几个是正确的？Ⅰ．y=Acos（ωt-2πX／λ+Ф0）Ⅱ．y=Acos[2π（t／T-X／λ）+Ф0]Ⅲ．y=Acos[2π（γt-X／λ）+Ф0]（）
- A、Ⅰ
- B、Ⅰ、Ⅱ
- C、Ⅱ、Ⅲ
- D、Ⅰ、Ⅱ、Ⅲ
正确答案:D -
第20题：
处于原点（x=0）的一波源所发出的平面简谐波的波动方程为y=Acos（Bt-Cx），其中A、B、C皆为常数。此波的速度为（）；波的周期为（）；波长为（）；离波源距离为l处的质元振动相位比波源落后（）；此质元的初相位为（）。
正确答案:B/C；2π/B；2π/C；lC；-lC -
第21题：
单选题一平面简谐波沿x轴正向传播，已知波长λ，频率υ，角频率ω，周期T，初相Ф0，则下列表示波动方程的式子中，哪几个是正确的？Ⅰ．y=Acos（ωt-2πX／λ+Ф0）Ⅱ．y=Acos[2π（t／T-X／λ）+Ф0]Ⅲ．y=Acos[2π（γt-X／λ）+Ф0]（）AⅠ
BⅠ、Ⅱ
CⅡ、Ⅲ
DⅠ、Ⅱ、Ⅲ
正确答案： A解析： u=λγ，ω=2πγ。 -
第22题：
单选题一平面简谐波沿x轴正向传播，振幅A＝0.02m，周期T＝0.5s，波长λ＝100m，原点处质元初相位φ＝0，则波动方程的表达式（ ）。[2012年真题]Ay＝0.02cos2π（t/2－0.01x）（SI）
By＝0.02cos2π（2t－0.01x）（SI）
Cy＝0.02cos2π（t/2－100x）（SI）
Dy＝0.002cos2π（2t－100x）（SI）
正确答案： A解析：
沿x轴正向传播的波动方程表达式为：y＝Acos[ω（t－x/u）＋φ0]。又u＝λ/T，ω＝2π/T，故波动方程写为：y＝Acos[2π（t/T－x/λ）＋φ0]。由于A＝0.02m，T＝0.5s，λ＝100m，φ0＝0，代入波动方程公式可得：y＝0.02cos2π（2t－0.01x）（SI）。