将质量为m的物体在空气中竖直上抛,初速度为vo,若空气阻力与物体的速度V(t)(t是时间)成正比,比例系数为k,g为重力加速度.V(t)所满足的微分方程及初始条 件是( ).A. B. C. D.
题目

B.
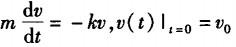
C.
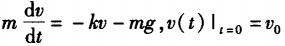
D.

相似考题
更多“将质量为m的物体在空气中竖直上抛,初速度为vo,若空气阻力与物体的速度V(t)(t是时间)成正比,比例系数为k,g为重力加速度.V(t)所满足的微分方程及初始条 件是( ).”相关问题
-
第1题:
潜水艇在水中下沉时,其所受阻力与下沉速度成正比,若潜艇由静止状态开始下沉,则下列哪个方程是x(t)(路程是时间的函数)所满足的微分方程(其中K是比例系数,g为重力加速度)? 答案:D解析:提示:设潜艇下沉方向为正向,利用牛顿第二定律列微分方程,分析受力情况,由重力
答案:D解析:提示:设潜艇下沉方向为正向,利用牛顿第二定律列微分方程,分析受力情况,由重力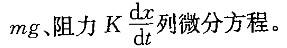
-
第2题:
以不同的初速度将两个物体同时竖直向上抛出并开始计时。一个物体所受空气阻力可忽略,另一个物体所受空气阻力大小与物体速率成正比。下列用虚线和实线描述两物体运动的v-t图象,可能正确的是( )。 答案:D解析:一个物体在竖直上抛时不受空气阻力,向上做匀减速直线运动至最高点再向下做自由落体运动,V一t图象是倾斜向下的直线,四个选项(虚线)均正确;另一个物体所受空气阻力大小与物体速率成正比,上升时阻力方向竖直向下,V减小,加速度减小,对应的口一t图线的斜 率减小,A错误;下落时阻力方向竖直向上,V增大,加速度减小,在最高点时v=0,a=g,对应的。一t图线与x轴的交点,其斜率应该等于g,即过交点的切线应该与竖直上抛运动的直线(虚线)平行.选项D正确。
答案:D解析:一个物体在竖直上抛时不受空气阻力,向上做匀减速直线运动至最高点再向下做自由落体运动,V一t图象是倾斜向下的直线,四个选项(虚线)均正确;另一个物体所受空气阻力大小与物体速率成正比,上升时阻力方向竖直向下,V减小,加速度减小,对应的口一t图线的斜 率减小,A错误;下落时阻力方向竖直向上,V增大,加速度减小,在最高点时v=0,a=g,对应的。一t图线与x轴的交点,其斜率应该等于g,即过交点的切线应该与竖直上抛运动的直线(虚线)平行.选项D正确。 -
第3题:
将质量为m的物体在空气中竖直上抛,初速度为V0,若空气阻力与物体的速度v(t)(t是时间)成正比,比例系数为K,g为重心加速度。则下列哪个方程是v(t)所满足的微分方程()?
- A、m(dv/dt)=Kv
- B、m(dv/dt)=-Kv
- C、m(dv/dt)=-Kv-mg
- D、m(dv/dt)=-Kv+mg
正确答案:C -
第4题:
不计空气阻力,以一定的初速度竖直上抛一物体,从抛出至回到抛出点的时间为t,现在物体上升的最大高度的一半处设置一块挡板,物体撞击挡板前后的速度大小相等、方向相反,撞击所需时间不计,则这种情况下物体上升和下降的总时间约为()
- A、0.5t
- B、0.4t
- C、0.3t
- D、0.2t
正确答案:C -
第5题:
在不计空气阻力的情况下,某物体以30m/s的初速度从地面竖直上抛,则(重力加速度g取10m/s2)()
- A、前4s内物体的平均速度大小为10m/s
- B、前4s内物体的位移大小为50m
- C、第2s末到第4s末物体的平均速度为5m/s
- D、第2s内和第4s内物体的速度改变量不相同
正确答案:A -
第6题:
某物体以40m/s的初速度竖直上抛,不计空气阻力,g取10m/s2,则抛出后5s内物体的()
- A、速度改变量的大小为45m/s
- B、平均速度大小为15m/s,方向向上
- C、位移大小为75m,方向向下
- D、路程为85m
正确答案:B,D -
第7题:
不计空气阻力,以一定的初速度竖直上抛的物体,从抛出至回到抛出点的时间为t,现在物体上升的最大高度的一半处设置一块挡板,物体撞击挡板前后的速度大小相等、方向相反,撞击所需时间不计,则这种情况下物体上升和下降的总时间约为()
- A、0.5t
- B、0.4t
- C、0.3t
- D、0.2t
正确答案:C -
第8题:
一物做匀变速直线运动,其位移与时间关系是:s=5+2t+4t²(m),由此可知()
- A、物体的初速度为5m/s
- B、物体的初速度是4m/s
- C、物体的加速度是4m/s²
- D、物体的加速度是8m/s²
正确答案:D -
第9题:
一个物体位移与时间的关系为s=5t+5t2(s以m为单位,t以s为单位),下列说法中正确的是()
- A、这个物体的初速度是2.5m/s
- B、这个物体的加速度大小是10m/s2
- C、这个物体的初速度是10m/s
- D、这个物体加速度方向一定与初速度方向相反
正确答案:B -
第10题:
以初速度v0将一物体斜向上抛出,抛射角为θ〉45°,不计空气阻力,在t=v0(sinθ-cosθ)/g时刻该物体的()
- A、法向加速度为g
- B、法向加速度为-√2/3g
- C、切向加速度为-√3/2g
- D、切向加速度为-√2/3g
正确答案:D -
第11题:
单选题将质量为m的物体在空气中竖直上抛,初速度为V0,若空气阻力与物体的速度v(t)(t是时间)成正比,比例系数为K,g为重心加速度。则下列哪个方程是v(t)所满足的微分方程()?Am(dv/dt)=Kv
Bm(dv/dt)=-Kv
Cm(dv/dt)=-Kv-mg
Dm(dv/dt)=-Kv+mg
正确答案: A解析: 设竖直上抛方向为正向,利用牛顿第二定律分析上抛运动的受力列微分方程。 -
第12题:
填空题以初速度v0平抛一个质量为m的物体,从抛出开始计时,t秒时间内物体的动量变化的大小为____kg·m/s.正确答案: mgt解析:
平抛运动,水平速度不变,竖直方向做初速度为0加速度为g的匀加速运动,t秒后,竖直方向的速度为gt,所以动量变化的大小为mgt kg·m/s. -
第13题:
如图所示,在光滑水平地面上,一质量为M的物体以v0的速度做匀速直线运动,把另一质量为m的物体轻放在M上,由于物体间的摩擦作用,经t秒后两者以共同速度运动。求:
(1)两物体共同运动速度的大小v;
(2)在时间t内,m所受摩擦力的大小。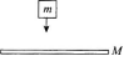 答案:解析:
答案:解析: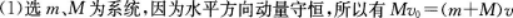

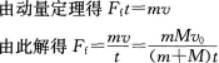
-
第14题:
一质量为m的小球,从高出水面h处的A点自由落下,如图6所示。已知小球在水中受到的黏滞阻力与小球的运动速率v成正比(比例系数为k)。设小球在水中的浮力忽略不计,以小球恰好垂直落入水中时为计时起点(t=O)。求小球在水中的运动速率v与时间t的关系: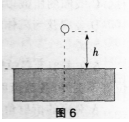 答案:解析:设小球从高出水面h处落入水中的速度为”v0”
答案:解析:设小球从高出水面h处落入水中的速度为”v0”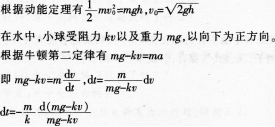
对两边进行积分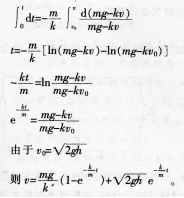
-
第15题:
某物体以30m/s的初速度竖直上抛,不计空气阻力,g取10m/s2.5s内物体的()
- A、路程为65m
- B、位移大小为25m,方向向上
- C、速度改变量的大小为10m/s
- D、平均速度大小为13m/s,方向向上
正确答案:A,B -
第16题:
在20m高处以初速度15m/s竖直上抛一物体,不计空气阻力,g取10m/s2,则物体离抛出点10m时,所经历的时间是()
- A、1s
- B、2s
- C、3s
- D、3.56s
正确答案:A,B,D -
第17题:
一行星的半径是地球半径的2倍,密度与地球的密度相同。在此行星上以一定的初速度竖直上抛一个质量为m物体,上升的高度为h,则在地球上以同样大小的初速度竖直上抛一质量为2m的物体,上升的高度为(空气阻力不计):()
- A、h
- B、2h
- C、3h
- D、4h
正确答案:B -
第18题:
物体以初速度v0竖直上抛,经3s到达最高点,空气阻力不计,g取10m/s2,则下列说法正确的是()
- A、物体上升的最大高度为45m
- B、物体速度改变量的大小为30m/s,方向竖直向上
- C、物体在第1s内、第2s内、第3s内的平均速度之比为5∶3∶1
- D、物体在1s内、2s内、3s内的平均速度之比为9∶4∶1
正确答案:A,C -
第19题:
从某高处将物体以30m/s的初速度竖直上抛,不计空气阻力,g取10m/s2.前5s内(物体未落地)物体的()
- A、路程为65m
- B、位移大小为25m,方向向上
- C、速度改变量的大小为10m/s
- D、平均速度大小为13m/s,方向向上
正确答案:A,B -
第20题:
一个物体位移与时间的关系为s=5t+5t²(位移以米为单位,时间以秒为单位),下列说法中正确的是()
- A、这个物体的初速度是2.5m/s
- B、这个物体的加速度大小是10m/s²
- C、这个物体的初速度是5m/s
- D、这个物体的加速度方向一定与初速度方向相反
正确答案:B,C -
第21题:
质量为M的车以速度v0沿光滑水平地面直线前进,车上的人将一质量为m的物体相对于车以速度u竖直上抛,则此时车的速度v=().
正确答案:V0 -
第22题:
问答题一质量为M的物体自空中落下,设空气的阻力的大小与落体的速度成正比(比例系数K>0),试求物体运动的路程与时间的函数关系。正确答案:
物体自空中落下的过程中,受到自身重力和空气对其产生的阻力,则由牛顿第二定律得md2s/dt2=mg-kds/dt,即d2s/dt2+(k/m)(ds/dt)=g。
对应的齐次方程d2s/dt2+(k/m)(ds/dt)=0的特征方程为r2+kr/m=0。
解得特征根为r1=0,r2=-k/m。
则对应齐次方程的通解为s(t)=C1+C2e-kt/m。
设s*(t)=At为非齐次方程d2s/dt2+(k/m)(ds/dt)=g的特解,将其代入方程得s*(t)=mgt/k。
则方程d2s/dt2+(k/m)(ds/dt)=g的通解为s(t)=C1+C2e-kt/m+mgt/k。
由s(0)=s′(0)=0得C1=-m2g/k2,C2=m2g/k2,则物体运动的路程与时间的函数关系为s=(e-kt/m-1)m2g/k2+mgt/k。解析: 暂无解析 -
第23题:
单选题已知一个物体在斜抛运动时斜抛角度为α(弧度),斜抛初速度为v,重力加速度为9.8,计算物体水平位移的步骤有:①计算物体飞行时间t=v?sinα/9.8②输入斜抛角度α和初速度v③输出变量s④计算水平位移量s=2w?t?cosα其正确的顺序是()。A③④①②
B①②③④
C②①④③
D②①③④
正确答案: A解析: 暂无解析
