设曲线y=ln(1+x2)，M是曲线上的点，若曲线在M点的切线平行于已知直线y-x+1=0，则点M的坐标是( )。 A.(-2，ln5) B.(-1，ln2) C.(1，ln2) D.(2，ln5)

题目
设曲线y=ln(1+x2)，M是曲线上的点，若曲线在M点的切线平行于已知直线y-x+1=0，则点M的坐标是( )。

A.(-2，ln5)
B.(-1，ln2)
C.(1，ln2)
D.(2，ln5)
相似考题

1.已知某点的高斯横坐标Y=13365759.13m,则该点横坐标的实际值为()m。

2.在空间直角坐标系中，已知点A（1，0，2），B(1，-3，1)，点M在y轴上，且M到A与到B的距离相等，则M的坐标是________。

3.设曲线y=y(x)上点P(0，4)处的切线垂直于直线x-2y+5=0，且该点满足微分方程y″+2y′+y=0，则此曲线方程为( )。A. B. C. D.

4.函数y=x²＋x－2,已知该曲线在点M处的切线斜率为3,则点M的坐标是(2,0)。()此题为判断题(对，错)。

参考答案和解析
答案：C
解析：
在D选项中，利用函数在一点的导数的几何意义及平行的已知条件确定点的坐标
更多“设曲线y=ln(1+x2)，M是曲线上的点，若曲线在M点的切线平行于已知直线y-x+1=0，则点M的坐标是( )。 ”相关问题

  • 第1题：

    已知直线L1过点M1(0，0，-1)且平行于X轴，L2过点M2(0，0，1)且垂直于XOZ平面，则到两直线等距离点的轨迹方程为( )。

    A.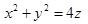
    B.
    C.
    D.

    答案：D
    解析：

  • 第2题：

    过点M0(-1，1)且与曲线2ex-2cosy-1 = 0上点(0，π/3)的切线相垂直的直线方程是：


    答案：C
    解析：
    点斜式求出直线方程。

  • 第3题：

    设曲线y=ax2+2x在点(1，a+2)处的切线与y=4x平行，则a=______．


    答案：
    解析：
    填1．因为y'(1)=2a+2=4，则a=1．

  • 第4题：

    设曲线y=x2+x-2在点M处切线的斜率为2，则点M的坐标为（）.


    答案：
    解析：

    【考情点拨】本题考查了曲线上一点处的切线的知识点．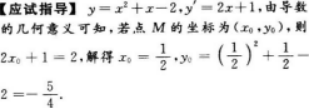

  • 第5题：

    曲线sin(xy)+ln(y-x)=x在点(0，1)处的切线方程是________.


    答案：1、y=x+1.
    解析：
    先求曲线sin(xy)+ln(y-x)=x在点(0，1)处切线斜率y'(0).等式sin(xy)+ln(y-x)=x两端对x求导得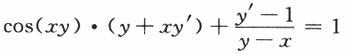

    在上式中令x=0，y=1得y'(0)=1，于是该曲线在点(0，1)处的切线方程为y-1=x，即y=x+1.

  • 第6题：

    设曲线y=y（x）过（0，0）点，M是曲线上任意一点，MP是法线段，P点在x轴上，已知MP的中点在抛物线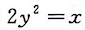，求此曲线的方程。


    答案：
    解析：

  • 第7题：

    设曲线y = ln(1+ x2), M是曲线上的点，若曲线在M点的切线平行于已知直线y-x+1= 0，则M点的坐标是（ ）。

    A. (-2,ln5) B. (-1，ln2) C. (1,ln2) D. (2,ln5)


    答案：C
    解析：

  • 第8题：

    在一条直线上有A、B两点，已知A、B点之间的水平距离是18m，A点高程是8m，B点高程是2m，则该直线的平距是1/3。


    正确答案:错误

  • 第9题：

    在高斯平面直角坐标系中，已知某点的通用坐标为x=3852321.456m，y=38436458.167m，则该点的自然坐标是（）

    • A、x=3852321.456m；y=8436458.167m
    • B、x=52321.456m；y=38436458.167m
    • C、x=3852321.456m；y=-436458.167m
    • D、x=3852321.456m；y=-63541.833m

    正确答案:D

  • 第10题：

    问答题
    某曲线α=20°32′20″，R=400M，l0=90M，求：（1）切线长T，曲线长L（2）缓和曲线总偏角δ0、缓和曲线切线角β0（3）若ZH点里程为DK11+903.19，求HZ点里程

    正确答案： （1）T=117.62m，L=233.39m，
    （2）δ0=2°08′55″，β0=6°26′45″
    （3）HZ点里程：DK12+136.68
    解析： 暂无解析

  • 第11题：

    单选题
    切线支距法测设圆曲线带有缓和曲线的曲线是以（）为坐标原点，以切线为X轴，过原点的半径为Y轴，利用缓和曲线和圆曲线上各点的X轴、Y轴坐标测设曲线。
    A

    ZH点或HZ点

    B

    HY点或YH点

    C

    QZ点

    D

    JD点


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    若供给曲线上每一点的点弹性都等于1，则供给曲线只能是一条（  ）。
    A

    过原点的曲线

    B

    过原点的直线

    C

    平行于横轴的直线

    D

    垂直于横轴的直线


    正确答案： C
    解析：

  • 第13题：

    在曲线x=t，y=t2，z=t3上某点的切线平行于平面x+2y+z=4，则该点的坐标为：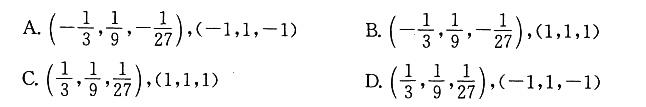


    答案：A
    解析：
    提示：切线平行于平面，那么切线的方向向量应垂直于平面的法线向量，利用向量垂直的条件得到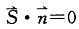，求出t值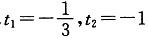，得到对应点的坐标。

  • 第14题：

    设曲线y=^e1?x2与直线x=-1的交点为P，则曲线在点P处的切线方程是（　　）

    A．2x-y+2=0
    B．2x+y+1=0
    C．2x+y-3=0
    D．2x-y+3=0

    答案：D
    解析：


    @##

  • 第15题：

    已知y=ax3在点x=1处的切线平行于直线y=2x-1，则a=______．


    答案：
    解析：
    填2/3．因为

  • 第16题：

    如图所示，已知A，B为直线L：y=mx-m+2与抛物线y=x2的两个交点。
    (1)直线ι经过一个定点C，试求出点C的坐标；(2分)
    (2)若m=-1，已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合)，且△ABP的面积为（3√13）/2，求点P的坐标。(6分)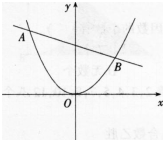


    答案：
    解析：
    (1)直线L：y=m(x-1)+2，当x=1时，y的取值与m无关，此时y=2，所以直线过定点(1，2)；

  • 第17题：

    设P是圆x2+y2=2上的一点，该圆在点P的切线平行于直线x+y+2=0，则点P的坐标为



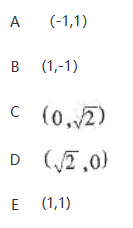    答案：E
    解析：

  • 第18题：

    以曲线起点、终点为坐标原点，以两端切线为x轴，过原点的曲线半径为y轴，根据曲线上各点的坐标进行测设的方法称为()。

    A、 切线支距法
    B、 偏角法
    C、 坐标法
    D、 切基线法

    答案：A
    解析：
    2018新教材P36 切线支距法：亦称为直角坐标法。它是以曲线起点ZH(或ZY)、终点（或YZ）为坐标原点，以两端切线为x轴，过原点的曲线半径为y轴，根据曲线上各点的坐标（图片）进行测设的。切线支距法适用于低等级公路。

  • 第19题：

    设y=f(x)可导，点a0=2为f(x)的极小值点，且f(2)=3，则曲线y=f(x)在点(2，3)处的切线方程为______．


    答案：
    解析：
    由于y=f(x)可导，点x0=2为f(x)的极小值点，由极值的必要条件可知f′(2)=0．曲线y=fx)在点(2，3)处的切线方程为y-3=f′(2)(x-2)=0，即y=3为所求切线方程．

  • 第20题：

    若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.


    正确答案:错误

  • 第21题：

    若供给曲线上每一点的点弹性都等于1，则供给曲线只能是一条（）

    • A、过原点的45线
    • B、过原点的直线 
    • C、平行于横轴的直线
    • D、垂直于横轴的直线

    正确答案:B

  • 第22题：

    填空题
    曲线y＝mx3＋1在点（1，1＋m）处切线的斜率为3，则m＝____．

    正确答案： 1
    解析：
    对y＝mx3＋1求导，得y′＝3mx2．因为曲线在点（1，1＋m）处切线的斜率为3，所以3＝3m·1，解得m＝1．

  • 第23题：

    单选题
    设竖曲线半径R=5000m，竖曲线上某点距离起点的距离为100m，则该点处的纵距为（）。
    A

    1.00m

    B

    2.00m

    C

    5.00m

    D

    10.00m


    正确答案： D
    解析： 暂无解析

相关内容