对某大学在校15000名学生的身高进行调查，从中随机抽取了100人进行抽样调查，测得的样本平均身高为l．66m，标准差为0．08m，总体平均身高未知，现以95%的置信水平对总体平均身高进行估计。

题目
对某大学在校15000名学生的身高进行调查，从中随机抽取了100人进行抽样调查，测得的样本平均身高为l．66m，标准差为0．08m，总体平均身高未知，现以95%的置信水平对总体平均身高进行估计。

相似考题

1.随机抽样调查甲、乙两地正常成年男子身高,得甲地身高的均值为175cm,乙地位179cm,经t检验得P&l随机抽样调查甲、乙两地正常成年男子身高，得甲地身高的均值为175cm，乙地位179cm，经t检验得PA.可认为两地正常成年男子平均身高相差不大B.甲、乙两地正常成年男子身高均值相差较大C.两地接受调查的正常成年男子平均身高不同D.可认为两地正常成年男子平均身高不同E.两地接受调查的正常成年男子平均身高差别较大

2.已知某小学一年级学生的平均体重为26kg,体重的标准差是3.2kg,平均身高2750px,标准差为150px,问体重与身高的离散程度哪个大()?A.体重B.身高C.离散程度一样D.无法比较

3.随机抽样调查甲、乙两地正常成年男子身高，得甲地身高的均值为175cm，乙地位179cm，经t检验得P＜0.05，差别有统计学意义。其结论为A、可认为两地正常成年男子平均身高相差不大B、甲、乙两地正常成年男子身高均值相差较大C、两地接受调查的正常成年男子平均身高不同D、可认为两地正常成年男子平均身高不同E、两地接受调查的正常成年男子平均身高差别较大

4.：对2000人进行身高测量，他们的身高总和为3400米，已知男性平均身高为175cm，女性平均身高为165cm，则参加身高调查的男性女性之比是多少?（ ）A．2：1B．1：1C．1：4D．1：2

更多“对某大学在校15000名学生的身高进行调查，从中随机抽取了100人进行抽样调查，测得的样本平均身高为l．66m，标准差为0．08m，总体平均身高未知，现以95%的置信水平对总体平均身高进行估计。”相关问题

  • 第1题：

    为了研究儿童的成长发育状况,随机抽取了36名儿童,测得平均身高为120CM,标准差为9,抽样标准误差为 1.5,则下列各项中正确的是( )。

    A.抽样标准误差是样本均值的标准差

    B.抽样标准误差是总体数据的标准差

    C.抽样标准误差是抽样产生的实际误差

    D.抽样标准误差是样本数据的标准差


    参考答案：A


  • 第2题：

    随机抽样调查甲、乙两地正常成年男子身高,得甲地身高的均值为175cm,乙地为179cm,经t检验得P<α,差别有统计学意义。其结论为

    A、可认为两地正常成年男子平均身高相差不大

    B、甲、乙两地正常成年男子身高均值相差较大

    C、两地接受调查的正常成年男子平均身高不同

    D、可认为两地正常成年男子平均身高不同

    E、两地接受调查的正常成年男子平均身高差别较大


    参考答案：D

  • 第3题：

    某种零件的长度服从正态分布。已知总体标准差σ=1．5，从总体中抽取200个零件组成样本，测得它们的平均长度为8．8厘米。试估计在95%置信水平下，全部零件平均长度的置信区间。


    正确答案：
    已知n=200，ψ=8．8，1-α=0．95，α=0．05， 
    当=0．025时，zα/2=z0．025=1．96
    根据题意，该题为双侧估计，μ的置信区间为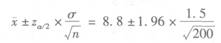 

    所以，总体均值μ在0．95置信水平下的置信区间为(8．59，9．01)

  • 第4题：

    在一次体检中，测了学生的身高水平。身高不超过160cm的有30名学生，平均身高为155cm；身高不低于180cm有45名学生，平均身高183cm；身高超过160cm的平均身高为175cm；身高低于180cm的平均身高172cm。请问此次学生的平均身高约为：

    A.172cm
    B.173cm
    C.174cm
    D.175cm

    答案：B
    解析：
    第一步，本题考查平均数问题，用方程法解题。
    第二步，设身高160cm—180cm之间的学生有x人，他们的总身高为y?cm。由题意有：y+45×183=175×（x+45）①，y+30×155=172×（x+30）②，联立解得x＝290，y＝50390。
    第三步，此次体检学生的平均身高约为（30×155＋50390＋45×183）÷（30＋290＋45）≈173cm。
    因此，选择B选项。

  • 第5题：

    某小学一年级学生的平均体重为25千克，体重的标准差是3.7千克；平均身高是110厘米，标准差为6.2厘米。结论正确的是

    A.体重比身高离散程度大
    B.身高比体重离散程度大
    C.体重和身高的离散程度无法比较
    D.身高和体重的离散程度一样大

    答案：A
    解析：
    可用变异系数对同一团体不同观察值的离散程度进行比较。本题申体重的cv值等于14.8%，而身高的CV值等于5.64%。因此该小学一年级学生体重的离散程度大于身高的离散程度。

  • 第6题：

    总体为正态分布、方差σ2未知。 样本量n = 20、样本的平均值为χ、标准差为 S ，当置信水平 为1-α时，总体均值μ的置信区间为（）。


    正确答案:χ±tα/2(20-1)S/√20

  • 第7题：

    随机从某地人口总体中，抽得100人构成样本，测得100人的平均身高为168cm。又据经验和以往资料知身高服从正态分布，身高的标准差为4cm，问在1%和5%的显著性水平下，是否可认为人口总体的平均身高为167cm。


    正确答案: 在0.01的的显著性水平下认为该地人口的平均身高为167；在0.05的显著性水平下，不能接受该地人口的平均身高为167。

  • 第8题：

    某地区成年男子2002年平均身高为1.70米，今测得该地区100名成年男子身高为1.72±0.04米，由此可知（）。

    • A、该地区成年男子身高平均增高了0.02米
    • B、该地区成年男子身高较2002年有明显增长
    • C、该地区成年男子身高与2002年相比无明显变化
    • D、该地区成年男子身高95％的置信区间为（1.72±1.96×0.04/10）
    • E、该地区成年男子身高99％的置信区间为（1.72±1.96×0.04/10）

    正确答案:D

  • 第9题：

    小儿身材矮小的诊断标准是（）

    • A、身高低于平均身高的2个标准差以下
    • B、身高低于平均身高的3个标准差以下
    • C、身高低于平均身高的5个标准差以下
    • D、身高低于同龄、同性别正常小儿生长曲线第3百分位数以下
    • E、身高低于同龄、同性别正常小儿生长曲线第5百分位数以下

    正确答案:A,D

  • 第10题：

    单选题
    随机抽样调查甲、乙两地正常成年男子身高，得甲地身高的均值为175cm，乙地为179cm，经t检验得P<α，差别有统计学意义。其结论为（）。
    A

    可认为两地正常成年男子平均身高相差不大

    B

    甲、乙两地正常成年男子身高均值相差较大

    C

    两地接受调查的正常成年男子平均身高不同

    D

    可认为两地正常成年男子平均身高不同

    E

    两地接受调查的正常成年男子平均身高差别较大


    正确答案： A
    解析： 两样本均数的t检验，是为了检验两样本均数所属的总体均数有无差别，并不能表示相差有多大。

  • 第11题：

    多选题
    小儿身材矮小的诊断标准是（）
    A

    身高低于平均身高的2个标准差以下

    B

    身高低于平均身高的3个标准差以下

    C

    身高低于平均身高的5个标准差以下

    D

    身高低于同龄、同性别正常小儿生长曲线第3百分位数以下

    E

    身高低于同龄、同性别正常小儿生长曲线第5百分位数以下


    正确答案： D,B
    解析： 暂无解析

  • 第12题：

    对成年组和幼儿组身高资料分组，计算得知成年组的平均身高为160.83cm，标准差为5.22cm;幼儿组的资料如下：

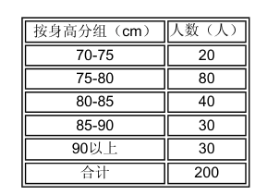
    (1)计算幼儿组的平均身高是___cm，标准差是___cm;

    (2)成年组、幼儿组的身高的标准差系数分别为___、___;(计算结果用小数表示，不用百分数。)(3)___的平均身高的代表性高。

    注：最后结果均取3位小数。按身高分组(cm)人数(人)


    参考答案：81.750,6.180,0.032,0.076,成年组

  • 第13题：

    某地调查18岁男大学生110名，身高的平均数为171cm，身高的标准差为4.10cm。体重的平均数为55.18kg，体重的标准差为4.12kg欲比较两指标变异程度的大小，可采用A、中位数

    B、几何均数

    C、变异系数

    D、标准差

    E、算术均数

    若评价此110名大学生的身高与当地18岁其他人群身高有无差别需进行A、样本均数与总体均数的显著性检验

    B、两个样本均数的显著性检验

    C、同一批对象处理前后的显著性检验

    D、秩和检验

    E、无法评价

    如果进行显著性检验此资料的自由度（v）为A、110

    B、109

    C、108

    D、18

    E、171


    参考答案：问题 1 答案：C


    问题 2 答案：A


    问题 3 答案：B

  • 第14题：

    ● 为了调查某学校 3000名学生的身高，抽取了 100 名学生进行身高测量，以下叙述中正确的是 （23） .

    （23）

    A．测量的总体是 3000 名学生

    B．测量的样本是 100 名学生

    C．测量的个体是每个学生

    D．样本的容量是 100


    正确答案：D

  • 第15题：

    对某大学在校15000名学生的身高进行调查，从中随机抽取了100人进行抽样调查，测得的样本平均身高为1．66m，标准差为0．08m，总体平均身高未知，现以95％的置信水平对总体平均身高进行估计。


    答案：
    解析：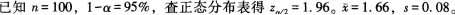


    由于总体方差未知，但为大样本，可用样本方差来代替总体方差。因此




    即以-95％的置信水平推断该校大学生总体平均身高在1．64m至1．68m之间。

  • 第16题：

    某超市想要估平均金额，采取简单随机方式抽取49名顾客进行调查。假定从正态分布，且标准差为15元。如果样本均值为120元求总体均值95%的置信区间。

    略

  • 第17题：

    为了估计全国高中学生的平均身高，从20个城市选取了100所中学进行调查在该项研究中，研究者感兴趣的总体是（）

    • A、100所中学
    • B、20个城市
    • C、全国的高学中生
    • D、100所中学的高中学生

    正确答案:C

  • 第18题：

    从5000名学生中抽查200名测得平均身高为1.65m抽样平均误差为0.05m，试以95%的把握程度推算全部学生平均身高的可能范围。若200名学生中女生数为50名，试以95%的概率，抽样成数平均误差为0.03，估计全部学生数中女生的比重的区间。


    正确答案:平均身高估计区间（1.55,1.75）, 女生比重估计区间:（19.12%.30.88%）

  • 第19题：

    青春期不同体型类型，成年后身高是（）

    • A、早熟型者身高>晚熟型者身高>平均型者身高
    • B、平均型者身高>晚熟型者身高>早熟型者身高
    • C、早熟型者身高<平均型者身高≤晚熟型者身高
    • D、早熟型者身高<晚熟型者身高<平均型者身高
    • E、早熟型者身高<平均型者身高=晚熟型者身高

    正确答案:C

  • 第20题：

    单选题
    某地调查18岁男大学生110名，身高的平均数为171cm，身高的标准差为4.10cm。体重的平均数为55.18kg，体重的标准差为4.12kg若评价此110名大学生的身高与当地18岁其他人群身高有无差别需进行（）
    A

    样本均数与总体均数的显著性检验

    B

    两个样本均数的显著性检验

    C

    同一批对象处理前后的显著性检验

    D

    秩和检验

    E

    无法评价


    正确答案： A
    解析： 暂无解析

  • 第21题：

    单选题
    青春期不同体型类型，成年后身高是（　　）。
    A

    早熟型者身高＜平均型者身高≤晚熟型者身高

    B

    早熟型者身高＜晚熟型者身高＜平均型者身高

    C

    平均型者身高＞晚熟型者身高＞早熟型者身高

    D

    早熟型者身高＞晚熟型者身高＞平均型者身高

    E

    早熟型者身高＜平均型者身高＝晚熟型者身高


    正确答案： C
    解析：
    早熟型者由于生长期短、身高增长量少，因此成年后身高低于平均水平；晚熟型者因为有较晚的生长突增和较长的生长期，以及青春期结束也晚，导致成年后身高达到平均水平，甚至高于平均水平。

  • 第22题：

    填空题
    总体为正态分布、方差σ2未知。 样本量n = 20、样本的平均值为χ、标准差为 S ，当置信水平 为1-α时，总体均值μ的置信区间为（）。

    正确答案： χ±tα/2(20-1)S/√20
    解析： 暂无解析

相关内容