2001个球平均分给若干个人，恰好分完。若有一个人不参加分球，则每人可以多分2个，而且球还有剩余；若每人多分3个，则球的个数不够，原来每人平均分到多少个球? A．87 B．56 C．63 D．69

题目

2001个球平均分给若干个人，恰好分完。若有一个人不参加分球，则每人可以多分2个，而且球还有剩余；若每人多分3个，则球的个数不够，原来每人平均分到多少个球? A．87 B．56 C．63 D．69

相似考题

1.10个球中3个红,7个绿,随机分给10个小朋友,每人一球。则最后三个分到球的小朋友中恰有一个得到红球的概率为()A、9/10B、147/1000C、441/1000D、21/40

2.袋子里有若干个球，小明每次拿出其中的一半再放回一个球，一共这样做了五次，袋中还有3个球，问原来袋中有多少个球?A．18B．34C．66D．158

3.甲乙两人共有100个玻璃球，若把甲的玻璃球的四分之一给乙，乙将比甲多九分之七，则甲原来有多少个玻璃球?A．40B．48C．56D．60

4.袋子里红球与白球的数量之比为19:13，放入若干个红球后，红球与自球的数量之比变为5:3，再放入若干个白球后，红球与白球的数量之比为13:11，已知放入的红球比白球少80个。那么原来袋子里共有多少个球?A．650B．720C．840D．960

更多“2001个球平均分给若干个人，恰好分完。若有一个人不参加分球，则每人可以多分2个，而且球还有剩余；若每人多分3个，则球的个数不够，原来每人平均分到多少个球? A．87 B．56 C．63 D．69”相关问题

  • 第1题：

    一堆玩具分给若干个小朋友，若每人分3件，则剩余4件；若前面每人分4件，则最后一人得到的玩具不足3件。求小朋友的人数与玩具数。

  • 第2题：

    有红球和绿球若干个，如果按每组1个红球2个绿球分组，绿球恰好够用，但剩5个红球；如果按每组3个红球5个绿球分组，红球恰好够用，但剩5个绿球，则红球和绿球共有（ ）个。

    A．122

    B．125

    C．130

    D．132


    正确答案：B
    设第一次分a组，第二次分b组，则依题，a+5=3b，2a=5b+5，解得a=40，6=15。故计算得红球为45个，绿球为80个，共有125个，故选B。

  • 第3题：

    箱子里有红、白两种玻璃球，红球是白球的3倍少2个。每次从箱子里取出7个白球、13个红球，经过若干次后，箱子里剩下6个白球，72个红球，那么，原来箱予里红球比白球多多少个？（ ）

    A．102

    B．104

    C．106

    D．108


    正确答案：D
    D[解析]假设箱子里原来有白球x个，那么红球为（3x-2）个，依题意有（x-6）÷7=（3x-2-72）÷13，解得x=55，所以原来红球比白球多3×55-2-55=108（个）。故选D。

  • 第4题：

    ：将铅笔若干支分给学生数人，若每人分10支则余48支；若每人分13支则差24支，问每人分几支正好分完？（ ）。

    A．12

    B．11

    C．10

    D．14


    正确答案：A

    设共有x名学生，则10x+48=13x一24，解得x=24，则共有24×10+48＝288支铅笔，要正好分完，每人应分铅笔288÷24=12(支)。

  • 第5题：

    数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
    一群学生进行篮球投篮测验，每人投10次，按每人进球数统计的部分情况如下表：

    如果知道至少投进3个球的人平均投进6个球，投进不到8个球的人平均投进3个球。问：共有多少人参加测验?（）
    A.43
    B.55
    C.61
    D.73


    答案：A
    解析：
    设有x人参加测验，由投中的总球数相等这一条件可列方程：
    1×5+2×4+(x-7-5-4)×6=(x-3-4-1)×3+8×3+9×4+10×1
    解得x=43，即有43人参加测验。

  • 第6题：

    甲乙两人共有100个玻璃球，若把甲的玻璃球的四分之一给乙，乙将比甲多九分之七，则甲原来有多少个玻璃球?( )


    A. 40
    B. 48
    C. 56
    D. 60

    答案：B
    解析：
    解题指导： 由“乙将比甲多九分之七”，设此时甲9份，乙9+7=16份。则100个球是25份，每份4个。甲原来有9÷（1- 1/4）=12份，即48个。故答案选B。

  • 第7题：

    一个暗箱装有12个编号从1到12的乒乓球，甲、乙、丙三人轮流从暗箱中摸球，每人每次摸一个球且不放回。将所有球摸完后，三人所摸出的球上的编号之和相等，并且甲摸出了1号球和3号球，乙摸出了6号球和11号球。丙摸出的球编号最大为多少？

    A.7
    B.8
    C.9
    D.10

    答案：C
    解析：
    第一步，本题考查其他杂题。
    第二步，根据题意可知12个球的数字之和为78，由于每个人摸到四个球且编号之和相等，则每人摸到的编号之和为26；甲摸到1号和3号则剩余两个只能为10和12号；乙摸到6号和11号，则剩余的可能为4号，5号或者为2号，7号；那么9号必为丙摸到的。故丙摸出编号最大的为9号。

  • 第8题：

    某中学举行颠足球比赛，比赛时长为2分钟。参加比赛的学生平均每人颠球260次，已知每人至少颠球240次，并且其中一人颠球324次，如果不把该学生计算在内，那么平均每人颠球252次。那么此次比赛颠球最快的学生最多颠了（）次。

    A．420
    B．368
    C．336
    D．252

    答案：C
    解析：
    设共有ｘ人参加比赛，则260ｘ＝324＋252（ｘ－1），解得ｘ＝9，当其余7个人都颠球240次时，颠球最快的学生颠的最多，为252×8－240×7＝336次。故本题选C。

  • 第9题：

    有红球和绿球若干个，如果按每组1个红球2个绿球分组，绿球恰好够用，但剩5个红球，如果按每组3个红球5个绿球分组，红球恰好够用，但剩5个绿球，则红球和绿球共有多少个？（）

    • A、120
    • B、135
    • C、140
    • D、125

    正确答案:D

  • 第10题：

    比赛中每人最多连续触球（）次。

    • A、2
    • B、3
    • C、4

    正确答案:A

  • 第11题：

    发飘球时若球飘晃则球一定是旋转的。


    正确答案:错误

  • 第12题：

    判断题
    发飘球时若球飘晃则球一定是旋转的。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    箱子里有红、白两种玻璃球。红球是向球的3倍少2个。每次从箱子里取出7个白球、13个红球，经过若干次后，箱子里剩下6个白球，72个红球，那么，原来箱子里红球比白球多多少个?（ ）

    A．102

    B．104

    C．106

    D．108


    正确答案：D
    假设箱子里原来有白球x个，那么红球为(3x--2)个，依题意有(x－6)÷7=(3x－2－72)÷13，解得x=55，所以原来红球比白球多3×55－2－55=108(个)。故选D。

  • 第14题：

    某班进行个人投篮比赛，受污损的下表记录了在规定时间内投进n个球的人数分布情况：

    同时，已知进球3个或3个以上的人平均每人投进3.5个球；进球4个或4个以下的人平均每人投进2.5个球。问投进3个球和4个球的各有(27)人?

    A．9，3

    B．6，7

    C．3，9

    D．7，6


    正确答案：A
    解析：这道题可以采用解方程的方法来做。假设投进3个球的有x个人，投进4个球的有y个人，那么
     
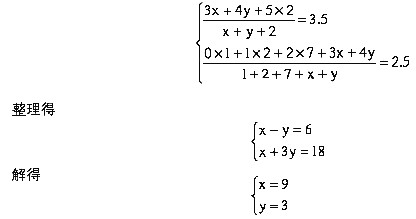
      则投进3个球的有9个人，投进4个球的有3个人。

  • 第15题：

    2001个球平均分给若干个人，恰好分完。若有一个人不参加分球，则每人可以多分2个．而且球还有剩余；若每人多分3个，则球的个数不够，则原来每人平均分到多少个球?

    A．87

    B．56

    C．63

    D．69


    正确答案：D
    由题意知，每人平均分得的球数应为2001的约数，2001=3×23×29排除8．C两项。若平均每人分87个．那么有2001÷87=23人。若有一人不参加分球，则2001÷22=90……21因此每人多分三个球还有剩余，与题干条件不符。只能选D。

  • 第16题：

    袋子中有若干黑球和白球。若取出一个黑球，则袋中黑球占总球数的 2/7；若取出两个白球，则袋中白球占 2/3。从原来袋中抽出3个球，其中有且仅有1个黑球的概率：

    A.低于20%
    B.在20%—40%之间
    C.在40%—60%之间
    D.高于60%

    答案：C
    解析：
    第一步，本题考查概率问题，用方程法解题。

  • 第17题：

    袋子里有若干个球，小明每次拿出其中的一半再放回一个球，一共这样做了五次，袋中还有3个球，问原来袋中有多少个球？( )


    A. 18
    B. 34
    C. 66
    D. 158

    答案：B
    解析：
    解题指导： 反推法，设第五次拿之前剩X：X/2+1=3，则X=4，依次推出剩6、10、18、34，故答案为B。

  • 第18题：

    某中学举行颠足球比赛，比赛时长为 2 分钟。 参加比赛的学生平均每人颠球 260 次，已 知每人至少颠球 240 次，并且其中一人颠球 324 次，如果不把该学生计算在内，那么平均每人 颠球 252 次。 那么此次比赛颠球最快的学生最多颠了（ ）次。

    A．420
    B．368
    C．336
    D．252

    答案：C
    解析：
    设共有ｘ人参加比赛，则260ｘ＝324＋252（ｘ－1），解得ｘ＝9，当其余7个人都颠球240次时，颠球最快的学生颠的最多，为252×8－240×7＝336次。

  • 第19题：

    袋子中有若干黑球和白球。若取出一个黑球，则袋中黑球占总球数的



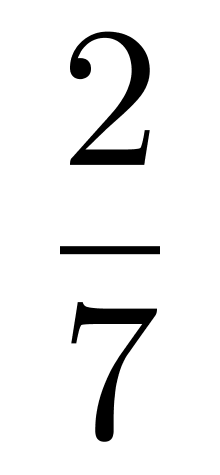
    ；若取出两个白球，则袋中白球占



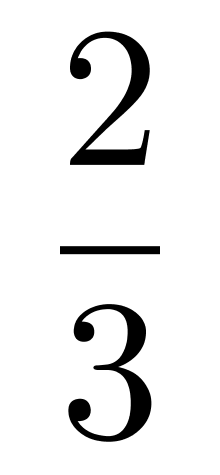
    。从原来袋中抽出3个球，其中有且仅有1个黑球的概率：

    A.低于20%
    B.在20%—40%之间
    C.在40%—60%之间
    D.高于60%

    答案：C
    解析：
    第一步，本题考查概率问题，用方程法解题。

  • 第20题：

    箱子里有乒乓球和网球若干，若每次取出乒乓球4个，网球2个，若干次后正好都取完；若每次取出乒乓球5个，网球3个，则两球取尽后，还剩余5个乒乓球，那么乒乓球和网球共有多少个：
    A40
    B45
    C53
    D58


    答案：B
    解析：
    解析
    第一种取法：每次取乒乓球4个，网球2个，每次取乒乓球是网球的2倍，则总数应被3整除；第二种取法，每次取乒乓球5个，网球3个，还剩余5个乒乓球，则总数减5，剩余球数应为8的倍数。观察选项只有B项符合。
    故正确答案为B。

  • 第21题：

    一袋中有2个黑球和若干个白球，现有放回地摸球4次，若至少摸到一个白球的概率是80/81，则袋中白球的个数是（）。


    正确答案:4

  • 第22题：

    排球垫球测试区域长为每人3米X3米。


    正确答案:正确

  • 第23题：

    单选题
    比赛中每人最多连续触球（）次。
    A

    2

    B

    3

    C

    4


    正确答案： B
    解析： 暂无解析

相关内容