把7个不能区分的苹果放到3个不同的盘子里(允许有空盘)，有多少种不同的放法?A．21B．18C．36D．38

题目

把7个不能区分的苹果放到3个不同的盘子里(允许有空盘)，有多少种不同的放法?

A．21

B．18

C．36

D．38

相似考题

1.有4个相同颜色的球放到不同编号的4个箱子里,不同的摆放方式共有________种。A．81B．256C．35D．12

2.有4个不同颜色的球放到不同编号的4个箱子里,不同的摆放方式共有________种。A．81B．256C．35D．12

3.10个大小相同的橘子放到3个不同的盘子里，允许有的盘子空着。请问一共有多少种不同的放法? A．286 B．220 C．120 D．66

4.把6个标有不同标号的小球放入三个大小不同的盒子里。大号盒子放3个，中号盒子放2个，小号盒子1个，问其有（ ）种放法A. 50B. 60C. 70D. 40

更多“把7个不能区分的苹果放到3个不同的盘子里(允许有空盘),有多少种不同的放法?A.21 B.18 C.36 D.38 ”相关问题

  • 第1题：

    数学运算：共10道题。你可以在草稿纸上运算，遇到难题，你可以跳过不做，待你有时间再返回来做。

    例题：84.78元、59.50元、121.61元、12.43元以及66.50元的总和是()。

    A．343.73B．343.83C．344.73D．344.82

    解答：正确答案为D。实际上你只要把最后一位小数加一下，就会发现和的最后一位数是

    2．只有D符合要求。就是说你应当动脑筋想出解题的捷径。

    请开始答题：

    6．把7个不能区分的苹果放到3个不同的盘子里(允许有空盘)，有多少种不同的放法?

    A．21

    B．18

    C．36

    D．38


    正确答案：C

    [答案]C。[解析]题中所述操作相当于：将10个不能区分的苹果放到三个盘子中(每个盘子至少一个苹果)，运用隔板法，

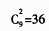
  • 第2题：

    把6个标有不同标号的小球放入三个大小不同的盒子里。大盒子放3个球，中号盒子放2个，小盒子放1个。问共有多少种放法?（　　）A.50  B.60  C.70　　　　D.40


    本题正确答案为B。本题是一个乘法原理与组合综合运用的问题。首先，把球放入盒子需分三步走，这需用乘法原理。其次，放入盒中的球不计顺序，这是一个组合问题，因此，综合以上两点可知，共有C36×C23×C11＝20×3×1＝60种放法

  • 第3题：

    小玉在收拾玩具，要把3个不同的皮球放到3个不同材质的箱子里，每个箱子最多只能放2个皮球，共有几种不同的放法?（ ）

    A．18

    B．21

    C．24

    D．27


    正确答案：C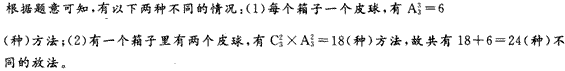

  • 第4题：

    把30个苹果放到6个抽屉中，问：是否存在一种放法，使每个抽屉中的苹果数都小于等于5？


    存在这样的放法。即：每个抽屉中都放5个苹果；

  • 第5题：

    某人到食堂去买饭，主食有三种，副食有五种，他主食和副食各买一种，共有多少种不同的买法?


    正确答案：15

  • 第6题：

    10只无差别的橘子放到3个不同的盘子里。允许有的盘子空着。请问一共有多少种不同的放法?

    A．36

    B．66

    C．54

    D．72


    正确答案：B
    此题相当于“13只橘子放到3个不同的盘子里，每个盘子至少有一个橘子，求有多少种放法?”此时可运用隔板法，相当于在13个橘子所形成的12个空格中插入两个隔板，有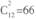HWOCRTEMP_ROC570种放法。

  • 第7题：

    有5本不同的书排成一排,其中甲、乙必须排在一起,丙、丁不能排在一起,则不同的排法共（ ）种

    A.12种
    B.24种
    C.36种
    D.48种
    E.60种

    答案：B
    解析：

  • 第8题：

    不同植物的（）有很多不同，但果实里都有（）。不同植物的种子也有很多（）。豌豆荚里的种子数不都是一样多，但荚里种子多少是有分布（）的。


    正确答案:果实；种子；不同；规律

  • 第9题：

    把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法（用K表示）？请设计一个算法计算K值（只需要计算K值，不用把具体的分法输出）。注意：5，1，1和1，5，1是同一种分法。


    正确答案: 例：M=7，N=3则有K=8
    可能的分法为：
    7，0，0
    6，1，0
    5，2，0
    4，3，0
    5，1，1
    4，2，1
    3，3，1
    3，2，2
    设f（m，n）为m个苹果，n个盘子的放法数目，则先对n作讨论，如果n>m，必定有n-m个盘子永远空着，去掉它们对摆放苹果方法数目不产生影响；即if（n>m）f（m，n）=f（m，m）当n<=m时，不同的放法可以分成两类：即有至少一个盘子空着或者所有盘子都有苹果，前一种情况相当于f（m，n）=f（m，n-1）；后一种情况可以从每个盘子中拿掉一个苹果，不影响不同放法的数目，即f（m，n）=f（m-n，n）.而总的放苹果的放法数目等于两者的和，即f（m，n）=f（m，n-1）+f（m-n，n）。边界条件为m=0或n=1时，只有一种放法。

  • 第10题：

    时分复用的基本原理（）。

    • A、把同一话路信号放到同一链路的不同时隙内。
    • B、把同一话路信号放到不同链路的同一时隙内。
    • C、把多个话路信号放到同一链路的不同时隙内。
    • D、把多个话路信号放到不同链路的同一时隙内。

    正确答案:C

  • 第11题：

    问答题
    把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法（用K表示）？请设计一个算法计算K值（只需要计算K值，不用把具体的分法输出）。注意：5，1，1和1，5，1是同一种分法。

    正确答案： 例：M=7，N=3则有K=8
    可能的分法为：
    7，0，0
    6，1，0
    5，2，0
    4，3，0
    5，1，1
    4，2，1
    3，3，1
    3，2，2
    设f（m，n）为m个苹果，n个盘子的放法数目，则先对n作讨论，如果n>m，必定有n-m个盘子永远空着，去掉它们对摆放苹果方法数目不产生影响；即if（n>m）f（m，n）=f（m，m）当n<=m时，不同的放法可以分成两类：即有至少一个盘子空着或者所有盘子都有苹果，前一种情况相当于f（m，n）=f（m，n-1）；后一种情况可以从每个盘子中拿掉一个苹果，不影响不同放法的数目，即f（m，n）=f（m-n，n）.而总的放苹果的放法数目等于两者的和，即f（m，n）=f（m，n-1）+f（m-n，n）。边界条件为m=0或n=1时，只有一种放法。
    解析： 暂无解析

  • 第12题：

    单选题
    4只小鸟飞入4个不同的笼子里去，每只小鸟都有自己的一个笼子（不同的鸟，笼子也不相同），每个笼子只能飞进一只鸟。若都不飞进自己的笼子里去，有多少种不同的飞法？（）。
    A

    7

    B

    8

    C

    9

    D

    10


    正确答案： D
    解析： 暂无解析

  • 第13题：

    n个完全一样的球放到m个有标志的盒子中，不允许有空盒，其中n≥m，则有多少种不同的方案()。

    A、C(n-1,m)

    B、C(n,m-1)

    C、C(n-1,m-1)

    D、C(n,m)


    参考答案：C

  • 第14题：

    （1）有三个不同的信箱，今有4封不同的信欲投其中，共有多少种不同的投法？


    正确答案：
     

  • 第15题：

    有六只水果箱，每箱里放的是同一种水果，其中只有一箱放的是香蕉，其余都是苹果和梨。已知所放水果的重量分别是1，3，12，21，17，35千克，且苹果总共的重量是梨的5倍，求香蕉有多少千克？

    A.3   B.21   C.17   D.35


    1+3+12+21+17+35=89
    苹果的重量是梨的5倍
    所以苹果+梨=6的倍数
    因此香蕉=17

     

    解析：六箱水果的总重量为1+3+12+21+17+35=89，因为苹果是梨的5倍，所以这两种水果的重量应为6的倍数，经验证，只有香蕉为17千克时，苹果和梨的总重量为72千克可以被6整除

  • 第16题：

    要把A、B、C、D四包不同的商品放到货架上，但是，A不能放在第一层，B不能放在第二层，C不能放在第三层，D不能放在第四层，那么，不同的放法共有( )种。

    A．6

    B．7

    C．8

    D．9


    正确答案：D
    12．【答案】D。解析：先放A，有3种放法，不妨设A放到了第二层，那么这时候再放B，也有3种放法，此时无论B放在哪里，C和D的位置都能确定，因此，不同的方法共有3×3=9种放法。

  • 第17题：

    把4朵不同的花放在5个不同的盒子中，有多少种放法？ （ ）

    A．24

    B．30

    C．60

    D．120


    正确答案：D
    排列组合问题，可考虑放第一朵时有5种选择，也就有5种可能，依次类推可知放第二朵时有4种可能，放第三朵时有3种可能，放第四朵时有2种可能，故共有5×4×3×2=120种放法，故选D。

  • 第18题：

    小玉在收拾玩具，要把3个不同的皮球放到3个不同材质的箱子里，每个箱子最多只能放2个皮球，共有几种不同的放法？（ ）

    A. 18
    B. 21
    C. 24
    D. 27

    答案：C
    解析：
    根据题意可知，有以下两种不同的情况：(1)每个箱子一个皮球，有A33=6 (种)方法；(2)有一个箱子里有两个皮球，有C32 × A32= 18(种)方法，故共有18 + 6 = 24(种 )不同的放法。

  • 第19题：

    有5个人排队,甲、乙必须相邻,丙不能在两头,则不同的排法共有（ ）.

    A.12种
    B.24种
    C.36种
    D.48种
    E.60种

    答案：B
    解析：

  • 第20题：

    将7个乒乓球放入3个同样的盒子里，允许有的盒子空着不放，共有（）种不同的放法。


    正确答案:8

  • 第21题：

    有多少种行业就有多少种不同的职业道德。


    正确答案:正确

  • 第22题：

    中餐转台式分菜操作结束后，应该把空盘子和分菜工具一并撤下。


    正确答案:正确

  • 第23题：

    问答题
    试判断下列各问题是用乘法原理还是用加法原理来解，并写出答案　 （1）从甲地到乙地可以乘火车，也可以乘轮船，还可以乘汽车．一天中有火车6班，轮船3班，汽车4班；一天中从甲地到乙地共有几种不同的走法？　 （2）从3本不同的语文书，4本不同的数学书，5本不同的外文书中任选一本共有几种不同的选法？　 （3）把5只不同的球任意放人4个不同的袋内，共有几种不同的放法？　 （4）加工某零件有三道工序，有8人能做第一道工序，有3人能做第二道工序，有2人能做第三道工序．从中选出3人加工此零件有多少种不同选法？

    正确答案： (1)完成“从甲地到乙地”这件事可以有乘火车、乘轮船、乘汽车这三类彼此独立的方法,因此应当运用加法原理.故不同的走法共有6+3+4=13(种).
    (2)完成“任选一本书”这件事可以有“选一本语文书”、“选一本数学书”、“选一本外文书”这三类方法,因此应当运用加法原理.故不同的选法共有3+4+5=12(种).
    (3)完成“把球放人袋内”这件事必须分五个步骤(即五个球一个一个地放人),因此应该运用乘法原理.故有4×4×4×4×4=1024(种).
    (4)完成“选出3人加工零件”这件事必须分三个步骤(即三道工序都要选出1人).因此用乘法原理,即有8×3×2=48(种).
    解析： 暂无解析

相关内容