10个大小相同的橘子放到3个不同的盘子里，允许有的盘子空着。请问一共有多少种不同的放法? A．286 B．220 C．120 D．66

题目

10个大小相同的橘子放到3个不同的盘子里，允许有的盘子空着。请问一共有多少种不同的放法? A．286 B．220 C．120 D．66

相似考题

1.有4个相同颜色的球放到不同编号的4个箱子里,不同的摆放方式共有________种。A．81B．256C．35D．12

2.有4个不同颜色的球放到不同编号的4个箱子里,不同的摆放方式共有________种。A．81B．256C．35D．12

3.甜点装盘时，下列说法正确的是( )。A.盘子应干净卫生、无破损B.除饰品外，所有主料、配料都不得露在盘子的外沿C.装盘后盘子四周允许有少量的汤汁D.盘子应是有相同风格的

4.请用python编程 据说古代有一个梵塔,塔内有3个底座A、B、C,A座上有64个盘子,盘子大小不等,大的在下,小的在上。有一个和尚想把这64个盘子从A座移动到C座,但每次只能允许移动一个盘子。在移动盘子的过程中可以利用B座,但任何时刻3个座上的盘子都必须始终保持大盘在下、小盘在上的顺序。如果只有一个盘子,则不需要利用B座,直接将盘子从A移动到C即可。 编写函数,接收一个表示盘子数量的参数和分别表

更多“10个大小相同的橘子放到3个不同的盘子里，允许有的盘子空着。请问一共有多少种不同的放法? A．286 B．220 C．120 D．66”相关问题

  • 第1题：

    数学运算：共10道题。你可以在草稿纸上运算，遇到难题，你可以跳过不做，待你有时间再返回来做。

    例题：84.78元、59.50元、121.61元、12.43元以及66.50元的总和是()。

    A．343.73B．343.83C．344.73D．344.82

    解答：正确答案为D。实际上你只要把最后一位小数加一下，就会发现和的最后一位数是

    2．只有D符合要求。就是说你应当动脑筋想出解题的捷径。

    请开始答题：

    6．把7个不能区分的苹果放到3个不同的盘子里(允许有空盘)，有多少种不同的放法?

    A．21

    B．18

    C．36

    D．38


    正确答案：C

    [答案]C。[解析]题中所述操作相当于：将10个不能区分的苹果放到三个盘子中(每个盘子至少一个苹果)，运用隔板法，

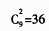
  • 第2题：

    把6个标有不同标号的小球放入三个大小不同的盒子里。大盒子放3个球，中号盒子放2个，小盒子放1个。问共有多少种放法?（　　）A.50  B.60  C.70　　　　D.40


    本题正确答案为B。本题是一个乘法原理与组合综合运用的问题。首先，把球放入盒子需分三步走，这需用乘法原理。其次，放入盒中的球不计顺序，这是一个组合问题，因此，综合以上两点可知，共有C36×C23×C11＝20×3×1＝60种放法

  • 第3题：

    六个盘子中各放有一块糖，每次从任选的两个盘子中各取一块放入另一个盘子中，这样至少要做多少次，才能把所有的糖都集中到一个盘子中?( )

    A．3次

    B．4次

    C．5次

    D．6次


    正确答案：B

  • 第4题：

    10只无差别的橘子放到3个不同的盘子里。允许有的盘子空着。请问一共有多少种不同的放法?

    A．36

    B．66

    C．54

    D．72


    正确答案：B
    此题相当于“13只橘子放到3个不同的盘子里，每个盘子至少有一个橘子，求有多少种放法?”此时可运用隔板法，相当于在13个橘子所形成的12个空格中插入两个隔板，有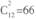HWOCRTEMP_ROC570种放法。

  • 第5题：

    将9个相同的小球放人A、B、C、D四个盒子中，允许有的盒子空着，一共有多少种不同的摆放结果?

    A．220

    B．84

    C．165

    D．120


    正确答案：A
    [答案] A。解析：在每个盒子中先放置一个小球，则问题转化为将13个小球放入四个盒子中而且不允许有空着的情况，可以采用隔板法，即在13个球的12个间隔处选择放下3个隔板将其分为4部分，C312=220。

  • 第6题：

    六个盘子中各放有一块糖，每次从任选的两个盘子中各取一块放入另一个盘子中，这样至少要做多少次，才能把所有的糖都集中到一个盘子中?

    A. 3
    B. 4
    C. 5
    D. 6

    答案：B
    解析：
    开始时是1，1，1，1，1，1，第二次变为0，0，3，1，1，1，第三次变为2，0，2，0，1，1，第三次变为4，0，1，0，0，1，第四次变为6，0，0，0，0，0。故答案为B。

  • 第7题：

    如果不堆叠，直径16厘米的盘子里最多可以放多少个边长为6厘米的正方体？（ ）

    A1
    B2
    C3
    D4


    答案：C
    解析：

  • 第8题：

    甜点装盘时，所有的主料、配料及饰品不得露在（）。

    • A、盘子的外沿
    • B、盘子边缘距中心1/2
    • C、盘子边缘距中心的1/3处
    • D、盘子的边缘距中心1/4处

    正确答案:A

  • 第9题：

    把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法（用K表示）？请设计一个算法计算K值（只需要计算K值，不用把具体的分法输出）。注意：5，1，1和1，5，1是同一种分法。


    正确答案: 例：M=7，N=3则有K=8
    可能的分法为：
    7，0，0
    6，1，0
    5，2，0
    4，3，0
    5，1，1
    4，2，1
    3，3，1
    3，2，2
    设f（m，n）为m个苹果，n个盘子的放法数目，则先对n作讨论，如果n>m，必定有n-m个盘子永远空着，去掉它们对摆放苹果方法数目不产生影响；即if（n>m）f（m，n）=f（m，m）当n<=m时，不同的放法可以分成两类：即有至少一个盘子空着或者所有盘子都有苹果，前一种情况相当于f（m，n）=f（m，n-1）；后一种情况可以从每个盘子中拿掉一个苹果，不影响不同放法的数目，即f（m，n）=f（m-n，n）.而总的放苹果的放法数目等于两者的和，即f（m，n）=f（m，n-1）+f（m-n，n）。边界条件为m=0或n=1时，只有一种放法。

  • 第10题：

    在腌黄瓜的时候，盘子里会剩出很多水，你能尝试做出解释吗？（）

    • A、因为外界溶液的浓度大于细胞液的浓度，所以黄瓜的细胞失水，盘子里才会剩出许多水
    • B、因为外界溶液的浓度小于细胞液的浓度，所以黄瓜的细胞失水，盘子里才会剩出许多水
    • C、因为盘子里放了许多盐，融化后产生了许多盐水。
    • D、因为外界溶液的浓度等于细胞液的浓度，所以黄瓜细胞里的水会流出来，盘子里才会剩出许多水

    正确答案:A

  • 第11题：

    问答题
    把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法（用K表示）？请设计一个算法计算K值（只需要计算K值，不用把具体的分法输出）。注意：5，1，1和1，5，1是同一种分法。

    正确答案： 例：M=7，N=3则有K=8
    可能的分法为：
    7，0，0
    6，1，0
    5，2，0
    4，3，0
    5，1，1
    4，2，1
    3，3，1
    3，2，2
    设f（m，n）为m个苹果，n个盘子的放法数目，则先对n作讨论，如果n>m，必定有n-m个盘子永远空着，去掉它们对摆放苹果方法数目不产生影响；即if（n>m）f（m，n）=f（m，m）当n<=m时，不同的放法可以分成两类：即有至少一个盘子空着或者所有盘子都有苹果，前一种情况相当于f（m，n）=f（m，n-1）；后一种情况可以从每个盘子中拿掉一个苹果，不影响不同放法的数目，即f（m，n）=f（m-n，n）.而总的放苹果的放法数目等于两者的和，即f（m，n）=f（m，n-1）+f（m-n，n）。边界条件为m=0或n=1时，只有一种放法。
    解析： 暂无解析

  • 第12题：

    单选题
    句子“我吃光了盘子里的菜。”中的补语“光”从语义上指向（）。
    A

    施事“我”

    B

    动词“吃”

    C

    名词“盘子”

    D

    受事“盘子里的菜”


    正确答案： B
    解析： 暂无解析

  • 第13题：

    如果不堆叠,直径16厘米的盘子里最多可以放多少个边长6厘米的正方体? A．1 B．2 C．3 D．4


    正确答案：C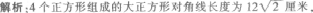
    大于圆的直径．因此最多放3个正方体,呈品字形放置。

  • 第14题：

    小玉在收拾玩具，要把3个不同的皮球放到3个不同材质的箱子里，每个箱子最多只能放2个皮球，共有几种不同的放法?（ ）

    A．18

    B．21

    C．24

    D．27


    正确答案：C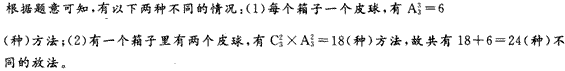

  • 第15题：

    六个盘子中各放有一块糖，每次从任选的两个盘子中各取一块放入另一个盘子中，这样至少要做多少次，才能把所有的糖都集中到一个盘子中?

    A．3

    B．4

    C．5

    D．6


    正确答案：B
    [答案] B[解析]此类操作性问题，要求最优的情况，需要细致的分析。按照题中的要求，每次从任选的两个盘子中各取一块放人另一个盘子中，开始时六个盘子是1、1、1、1、1、1，则第一次操作后一定是0、0、3、1、1、1。最后是0、0、0、0、0、6，则倒数第二次一定是0、0、0、1、1、4。现在需要考虑的就是0、0、3、1、1、1如何变成0、0、0、1、1、4，分析可知，从有三颗糖的盘子中取一粒，从有一颗糖的盘子中取一粒放在没有糖的盘子中，即变为2、0、2、0、1、1，然后从有两颗糖的盘子里取一粒，从有一颗糖的盘子里取一粒放在另一个有两颗糖的盘子里，变为了4、0、1、0、0、1，即达到了目的，共是4次操作。

  • 第16题：

    把7个不能区分的苹果放到3个不同的盘子里(允许有空盘)，有多少种不同的放法?

    A．21

    B．18

    C．36

    D．38


    正确答案：C
    [答案] C。解析：题中所述操作相当于：将10个不能区分的苹果放到三个盘子中(每个盘子至少一个苹果)，运用隔板法，C92=36。

  • 第17题：

    如果不堆叠，直径16厘米的盘子里最多可以放多少个边长6厘米的正方体?（ ）

    A．1

    B．2

    C．3

    D．4


    正确答案：C
    C
     

  • 第18题：

    如果不堆叠，直径16厘米的盘子里最多可以放多少个边长6厘米的正方体？

    A.l
    B.2
    C.3
    D.4

    答案：C
    解析：
    4个正方形组成的大正方形对角线长度为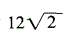厘米，大于圆的直径，因此最多放3个 正方体，呈品字形放置。

  • 第19题：

    小玉在收拾玩具，要把3个不同的皮球放到3个不同材质的箱子里，每个箱子最多只能放2个皮球，共有几种不同的放法？（ ）

    A. 18
    B. 21
    C. 24
    D. 27

    答案：C
    解析：
    根据题意可知，有以下两种不同的情况：(1)每个箱子一个皮球，有A33=6 (种)方法；(2)有一个箱子里有两个皮球，有C32 × A32= 18(种)方法，故共有18 + 6 = 24(种 )不同的放法。

  • 第20题：

    将7个乒乓球放入3个同样的盒子里，允许有的盒子空着不放，共有（）种不同的放法。


    正确答案:8

  • 第21题：

    甜点装盘时，下列说法正确的是（）。

    • A、盘子应干净卫生、无破损
    • B、除饰品外，所有主料、配料都不得露在盘子的外沿
    • C、装盘后盘子四周允许有少量的汤汁
    • D、盘子应是有相同风格的

    正确答案:A

  • 第22题：

    句子“我吃光了盘子里的菜。”中的补语“光”从语义上指向（）。

    • A、施事“我”
    • B、动词“吃”
    • C、名词“盘子”
    • D、受事“盘子里的菜”

    正确答案:D

  • 第23题：

    填空题
    纳西族的“____”是招待贵宾的方式，因使用大碗、小碗、盘子三种不同高度的餐具而得名。

    正确答案： 三叠水
    解析：
    三叠水，纳西人的满汉全席，因使用三套大小不同的餐具，即六个大碗、六个小碗和六个盘子，共十八道菜，所以又称作三叠水，在有贵客来访的时候，纳西人的最高礼仪就是“三叠水”。

相关内容