若干个同样的盒子排成一排，小明把五十多个同样的棋子分装在盒中，其中只有一只盒子没有装棋子，然后他外出了，小光从每个有棋子的盒子里各拿了一个棋子放在空盒内，再把盒子重新排了一下。小明回来后仔细查看了一下，没有发现有人动过这些盒子和棋子。问共有多少个盒子?A．20B．5C．9D．11

题目

若干个同样的盒子排成一排，小明把五十多个同样的棋子分装在盒中，其中只有一只盒子没有装棋子，然后他外出了，小光从每个有棋子的盒子里各拿了一个棋子放在空盒内，再把盒子重新排了一下。小明回来后仔细查看了一下，没有发现有人动过这些盒子和棋子。问共有多少个盒子?

A．20

B．5

C．9

D．11

相似考题

1.把48个球装在盒子里，每个盒子装的同样多，有几种装法？每种装法各需要几个盒子？如果有37个球呢？

2.将一个玩具放在蓝、红、黄三个盒子里,下面只有一条正确,那么玩具放在哪个盒子里?蓝色盒子:玩具在这个盒子里。红色盒子:玩具不在这个盒子里。黄色盒子:玩具不在蓝色盒子里。A.蓝色盒子B.黄色盒子C.红色盒子D.条件不充分，推导不出来

3.8个盒子排成一列，5个有标志的求放到盒子里面，每个盒子最多放一球，要求空盒子不相邻，问有多少种方案()。A、4800B、1200C、3600D、2400

4.某班同学在一次游艺晚，设有一个《动脑筋、育智慧》的节目。逻辑老师给这个节目出了一道题：下列七个盒子，哪个盒子有水果。七个盒子上分别写着一句话：第一个盒子上写道：“所有的盒子里都有水果。”第二个盒子上写道：“本盒子里没有水果。”第三个盒子上写道：“有些盒子里有山核桃。”第四个盒子上写道：“本盒子里没有苹果。”第五个盒子上写道：“所有的盒子里都没有山核桃。”第六个盒子上写道：“第四个盒子里放着一个苹果。”第七个盒子上写道：“有些盒子里没有水果。”在这七句话(每句表达一个性质命题)中，只有三句真话。你能确定哪个盒子里有水果吗?

更多“若干个同样的盒子排成一排，小明把五十多个同样的棋子分装在盒中，其中只有一只盒子没有装棋子，然后他外出了，小光从每个有棋子的盒子里各拿了一个棋子放在空盒内，再把盒子重新排了一下。小明回来后仔细查看了一下，没有发现有人动过这些盒子和棋子。问共有多少个盒子?A．20B．5C．9D．11”相关问题

  • 第1题：

    有16个盒子，里面放了27个小球，每个盒子放了1个、2个或者3个小球，其中放1个小球的盒子数与放2个和3个小球的盒子总数一样多，问：放2个小球的盒子有多少个? A．3 B．4 C．5 D．6


    正确答案：C
    放1个小球的盒子数与放2个和3个小球的盒子总数一样多，说明放1个小球的盒子有16÷2＝8个，那么放2个和3个小球的盒子也有8个且一共放小球27－8＝19个，因此，放2个小球的盒子有(8×3－19)÷(3－2)＝5个。

  • 第2题：

    三、小杨在中粮路演活动上获得了抽奖的机会，抽奖处有三个盒子:分别是红,绿,黄三种颜色。只有一个盒子有奖品。每个盒子上贴着一张纸条。三张纸条写着三句话,只有一句是真话。

    红盒子上写:奖品不在红盒子里

    绿盒子上写:奖品不在绿盒子里

    黄盒子上写:奖品不在红盒子里

    请问奖品在哪个盒子里?


    正确答案：

     

    答案三：

    在红盒子里。

  • 第3题：

    装某种产品的盒子有大、小两种，大盒每盒能装11个，小盒每盒能装8个，要把89个产品装入盒内，要求每个盒子都恰好装满，需要大、小盒子各多少个？

    A、3，7

    B、4，6

    C、5，4

    D、6，3


    正确答案：A
    选A
    普通解法：设大小盒分别为x、y个。则11x+8y=89。在自然数范围内解此不定方程，0≤x≤8，根据奇偶还得是个奇数，所以选择1、3、5、7代入发现，只有x=3可以得到自然数y=7
    特殊解法：直接代入。尾数为9的只有A。

  • 第4题：

    丁丁和宁宁各有一只盒子，里面都放着棋子，两只盒子里的棋子一共是270粒。丁丁从自己的盒子里拿出÷的棋子放入宁宁的盒子里后，宁宁盒子里的棋子数恰好增加亡。原来宁宁有棋子多少粒?（ ）

    A．180

    B．150

    C．120

    D．145


    正确答案：B
    根据题意，可知丁丁原有棋子的1/4恰好等于宁宁原有棋子的1/5。即丁丁原有棋子是宁宁的4/5。270÷(1+4/5)=150(粒)。

  • 第5题：

    装某种产品的盒子有大、小两种，大盒每盒能装11个，小盒每盒能装8个，要把89个产品装入盒内，要求每个盒子都恰好装满，需要大、小盒子各多少个?（ ）

    A．3，7

    B．4，6

    C．5，4

    D．6，3


    正确答案：A
    直接代入可得：3个大盒、7个小盒可装产品3×11+7×8=89个；4个大盒6个小盒可装产品4×11+6×8=92个；5个大盒4个小盒可装产品5×11+4×8=87个；6个大盒3个小金可装产品6×11+3×8=90个，所以选择A。

  • 第6题：

    有金、银、铜三个盒子，有一个硬币藏在其中一个盒子里，三个盒子上各贴着一张纸条，上面的提示分别是：(1)硬币在金盒子中；(2)硬币不在银盒子中； (3)硬币不在金盒子中。这三句话只有一句是真的。根据以上条件，硬币藏在哪个盒子中?
    A．硬币在金盒子中 B．硬币在银盒子中 C. 硬币在铜盒子中 D. 无确切答案


    答案：B
    解析：
    本题属于直言判断的对当关系中的矛盾推理题。题中（1）和（3）是矛盾关系，必有一真一假，则根据“这三句话只有一句是真的”可推得（2）是假的，则知道硬帀在银盒子中。

  • 第7题：

    一个盒子里有黑棋子和白棋子若干粒，若取出一粒黑子，则余下的黑子数与白子数之比为9：7，若放回黑子，再取出一粒白子，则余下的黑子数与白子数之比为7：5，那么盒子里原有的黑子数比白子数多：

    A.5枚
    B.6枚
    C.7枚
    D.8枚

    答案：C
    解析：
    棋子总数减1是9+7和7+5的倍数，因此设棋子总数为48n+1，48为16和12的最小公倍数。根据黑子数量得等式27n+1=28n，解得n=1。因此黑子有28枚，白子有21枚，黑子比白子多7枚。

  • 第8题：

    糖果游戏中，桌子上放着黄、绿、蓝、红色四只盒子，黄盒子上写着：糖果不在蓝盒子里。绿盒子上写着：糖果在红盒子或者 黄盒子里。蓝盒子上写着：糖果在此盒子里。红盒子上写着：糖果在绿盒子里。如果只有一个盒子里放了糖果，并且只有一个盒子上 写的是真话，则装了糖果的盒子是（ ）。

    A 、 黄盒子 B 、 绿盒子 C 、 蓝盒子 D 、 红盒子


    答案：C
    解析：
    只有一个盒子里放了糖果，并且只有一个盒子上写的是真话，意思是只有一个盒子上的话是真的，其他是假的。所以，黄盒子和蓝盒子是矛盾 的，所以它们中有一个说的为真话，绿盒子和红盒子的话是假的。所以糖果只能在蓝盒子里。

  • 第9题：

    A、B两个盒子共有棋子108颗，先从A盒子中取出1/4棋子放入B盒，再从B盒中取出1/4棋子放入A盒，这时两盒的棋子数相等。问A盒中原有棋子是多少？（）

    • A、40颗
    • B、48颗
    • C、52颗
    • D、60颗

    正确答案:B

  • 第10题：

    将7个乒乓球放入3个同样的盒子里，允许有的盒子空着不放，共有（）种不同的放法。


    正确答案:8

  • 第11题：

    单选题
    猜糖果游戏中桌子上放着黄绿蓝红色四个盒子，黄色的盒子上写着：糖果不在蓝盒子中 绿色盒子上写着：糖果在红盒或黄盒中 蓝色盒子上写着：糖果在此盒子中 红色盒子上写着：糖果在绿盒中 如果只有一只盒中装了糖果并且只有一只盒子上面写了真话，则装了糖果的盒子是（）。
    A

    黄盒

    B

    绿盒

    C

    蓝盒

    D

    红盒


    正确答案： B
    解析：

  • 第12题：

    问答题
    某中学高二班的一次联欢会上，进行了一次猜谜，这个谜是这样的：桌子上放了三只盒子：一只绿色，一只蓝色，一只红色。在每只盒子上都粘了一张纸条，纸条上写着不同的话：绿盒子上写着：糖果不在此盒中；蓝盒子上写着：糖果在此盒中；红盒子上写着：糖果不在蓝盒中。主持晚会的文娱委员说：“三只盒子中，只有一只盒子上的话是真的，其余两只盒子上的话都是假的，请大家通过这三句话来猜一猜糖果在哪一只盒子里，猜对的，请吃盒子里的糖。”李姗姗很快就猜出来了。请问：李姗姗是怎样猜出来的？

    正确答案： （考查普通逻辑基本规律的运用）糖果在绿盒子中。李姗姗是这样猜想的：蓝盒子上写的“糖果在此盒(即‘蓝盒’)中”和红盒子上写的“糖果不在蓝盒中”是相互矛盾的两句话，这两句话必有一真一假。根据已知条件，三个盒子中只有一句话为真，那么，这句真话一定存在于蓝、红盒子上所写的互相矛盾的两句话中，剩下的绿盒子上所写的“糖果不在此盒(即‘绿盒’)中”必然是假话。根据排中律，“糖果不在绿盒中”为假，则“糖果在绿盒中”必然为真。
    解析： 暂无解析

  • 第13题：

    将12个球放入3个盒子里，使每个盒子里球的数目是偶数，且没有空盒，问共有几种放法?（ ）

    A．10

    B．12

    C．8

    D．6


    正确答案：A
    设三个盒子所放的球的数量为(x，y，z)，则有(2，2，8)，(2，4，6)，(2，6，4)，(2，8，2)，(4，2，6)，(4，4，4)，(4，6，2)，(6，2，4)，(6，4，2)，(8，2，2)。共10种。本题选A。 

  • 第14题：

    A、B、C、D四个盒子中依次放有6、4、5、3个球。第l个小朋友找到放球最少的盒子，从其他盒子中各取一个球放入这个盒子；然后第2个小朋友找到放球最少的盒子，从其他盒子中各取一个球放入这个盒子……如此进行下去。当34位小朋友放完后，问B盒子中放有多少个球?（ ）

    A．4

    B．6

    C．8

    D．11


    正确答案：B

     

  • 第15题：

    装某种产品的盒子有大、小两种，大盒每盒装11个，小盒每盒装8个，要把89个产品装入盒内，要求每个盒子都恰好装满，需要大、小盒子各多少个？（ ）

    A．3、7

    B．4、6

    C．5、4

    D．6、3


    正确答案：A
    设需要大盒子x个，小盒子y个，列方程得：11x+8y=89(x，y均为非负整数)，为保证x、y一定符合要求，根据方程，可知x、y不可能等于0，且x最大为7，Y最大为9。据此讨论计算，可知当x=3，y=7时，方程恰好成立，则答案为A。

  • 第16题：

    有16个盒子。里面放了27个小球，每个盒子放了1个、2个或者3个小球，其中放1个小球的盒子数与放2个和3个小球的盒子总数一样多，问放2个小球的盒子有多少个?

    A．3

    B．4

    C．5

    D．6


    正确答案：C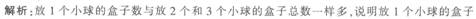



  • 第17题：

    黑白两个盒子中共有棋子193颗。若从白盒子中取出15颗棋子放入黑盒子中，则黑盒子中的棋子数是白盒子中棋子数的m（m为正整数）倍还多6颗。那么，黑盒子中原来的棋子至少有（ ）

    A．121颗 B．140颗 C．161颗 D．167颗

    答案：C
    解析：
    由题意可以得出，193-6=187=11×17，根据11、17均为质数这一特性，要使得黑盒子中的棋子数最少，令白盒子中的棋子数最大=17，则放入后黑盒子中的棋子数=193-17=176，放入前黑盒子中的棋子数=176-15=161。

  • 第18题：

    年终总结晚会上，有这样一个节目，桌子上有七个盒子，盒子里可能装有现金、钻石、黄金、支票中的一个或者多个，每个盒子上都写着一句话。第一个盒子：有些盒子里没有现金。第二个盒子:第四个盒子里有钻石。第三个盒子:所有的盒子里都有黄金。第四个盒子:本盒子里无钻石。第五个盒子:有些盒子里没有黄金。第六个盒子:本盒子里没有支票。第七个盒子：所有的盒子里都有现金。
    老总向员工们介绍，这七句话中有四句是假的，只有猜对的人才能获得该盒子里装的奖品。
    下列猜测一定正确的是（）。

    A.第一个盒子里有现金
    B.第二个盒子里有黄金
    C.第四个盒子里有钻石
    D.第六个盒子里有支票

    答案：D
    解析：
    第一个盒子与第七个盒子、第二个盒子与第四个盒子、第三个盒子与第五个盒子互为矛盾关系，必有三真三假。因为共有四句假话，所以第六个盒子上的话必为假，可知，第六个盒子里有支票。故答案选D。

  • 第19题：

    猜糖果游戏中桌上放着黄绿蓝红色四个盒子。
    黄色盒子上写着：糖果不在蓝盒中。
    绿色盒子上写着：糖果在红盒或黄盒中。
    蓝色盒子上写着：糖果在此盒中。
    红色盒子上写着：糖果在绿盒中。
    如果只有一个盒中装了糖果并且只有一个盒子上面写了真话，则装了糖果的盒子是()。

    A.黄盒
    B.绿盒
    C.蓝盒
    D.红盒

    答案：C
    解析：
    只有一个盒子上写了真话，而黄盒上写的糖果不在蓝盒中，与蓝盒上写的糖果在此盒中，两句话矛盾，可知两句话必然一真一假。综上可知，绿盒和红盒上写的都是假话，那么糖果不在红盒、黄盒、绿盒中，则糖果只能在蓝盒中。

  • 第20题：

    糖果游戏中，桌子上放着黄、绿、蓝、红四只盒子。
    黄盒子上写着：糖果不在蓝盒子
    绿盒子上写着：糖果在红盒子或者黄盒子
    蓝盒子上写着：糖果在此盒子里
    红盒子上写着：糖果在绿盒子里
    如果只有一个盒子放了糖果，并且只有一个盒子上写的是真话，则装糖果的是（　　）。


    A.黄盒子

    B.绿盒子

    C.蓝盒子

    D.红盒子

    答案：C
    解析：
    本题是真假推理题。“只有一个盒子放了糖果，并且只有一个盒子上写的是真话”，意思是只有一个盒子上写的话为真，其他为假。从四句话中可以看出黄盒子与蓝盒子的话是矛盾的，所以它们中有一个说的为真，绿盒子和红盒子的话必为假，即糖果一定不在红、黄、绿盒子里，只能是蓝盒子。

  • 第21题：

    两个盒子里都有糖果，一个盒子里的糖果数是奇数，另一个盒子里的糖果数是偶数。如果右边盒子里的糖果数乘3，左边盒子里的糖果数乘2，然后把两个数加起来，和是49。猜一猜哪个盒子里的糖果数是奇数（）

    • A、左边
    • B、右边
    • C、左右边都是
    • D、无法确定

    正确答案:B

  • 第22题：

    糖果游戏中，桌子上放着黄、绿、蓝、红四只盒子。 黄盒子上写着：糖果不在蓝盒子 绿盒子上写着：糖果在红盒子或者黄盒子 蓝盒子上写着：糖果在此盒子里 红盒子上写着：糖果在绿盒子里 如果只有一个盒子放了糖果，并且只有一个盒子上写的是真话，则装糖果的是（）。

    • A、黄盒子
    • B、绿盒子
    • C、蓝盒子
    • D、红盒子

    正确答案:C

  • 第23题：

    单选题
    A、B两个盒子共有棋子108颗，先从A盒子中取出1/4棋子放入B盒，再从B盒中取出1/4棋子放入A盒，这时两盒的棋子数相等。问A盒中原有棋子是多少？（）
    A

    40颗

    B

    48颗

    C

    52颗

    D

    60颗


    正确答案： D
    解析： 暂无解析

相关内容