8个盒子排成一列,5个有标志的求放到盒子里面,每个盒子最多放一球,要求空盒子不相邻,问有多少种方案()。A、4800B、1200C、3600D、2400
题目
8个盒子排成一列,5个有标志的求放到盒子里面,每个盒子最多放一球,要求空盒子不相邻,问有多少种方案()。
A、4800
B、1200
C、3600
D、2400
相似考题
更多“8个盒子排成一列,5个有标志的求放到盒子里面,每个盒子最多放一球,要求空盒子不相邻,问有多少 ”相关问题
-
第1题:
丁丁和宁宁各有一只盒子,里面都放着棋子,两只盒子里的棋子一共是270粒。丁丁从自己的盒子里拿出÷的棋子放入宁宁的盒子里后,宁宁盒子里的棋子数恰好增加亡。原来宁宁有棋子多少粒?( )
A.180
B.150
C.120
D.145
正确答案:B
根据题意,可知丁丁原有棋子的1/4恰好等于宁宁原有棋子的1/5。即丁丁原有棋子是宁宁的4/5。270÷(1+4/5)=150(粒)。 -
第2题:
64个小球放到18个盒子里,每个里面最多放6个,所有盒子里都有小球.问最少几个盒子里的小球数目相同?()[2008年招行真题]
A.2
B.3
C.4
D.5答案:C解析:利用抽屉原理,按题干要求每个盒子里都有小球。最多放6个。可以从1到6构造6个抽屉,则问题转化为至少有几个含小球数目相同的盒子在同一个抽屉里。因为共有18个盒子.18+6=3,故假设每个抽屉里有3个盒子的小球数目是相同的,故18个盒子里放的小球最多有3×(1+2+3+4+5+6)=63 -
第3题:
要把85个球放人若干个盒子中,每个盒子中最多放7个。问:至少有几个盒子中的球的数目相同?()
A. 2 B. 3 C. 4 D. 5答案:C解析:每盒放1,2,3,4,5,6,7个球,这样的七盒共放球:
1+2 + 3+4+5 + 6 + 7 = 28(个),85/28 = 3... 1。
所以至少有4个盒中的球数相同。故本题正确答案为C。 -
第4题:
有16个盒子。里面放了27个小球,每个盒子放了1个、2个或者3个小球,其中放1个小球的盒子数与放2个和3个小球的盒子总数一样多,问放2个小球的盒子有多少个?
A.3
B.4
C.5
D.6
正确答案:C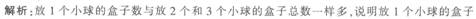

-
第5题:
数学运算。在这部分试题中,每道试题呈现一段表述数字关系的文字.要求你迅速、准确地计算出答案。
64个小球放到18个盒子里,每个里面最多放6个.所有盒子里都有小球,问最少几个盒子里的小球数目相同?()
A.2
B.3
C.4
D.5答案:C解析:利用抽屉原理,按题干要求每个盒子里都有小球。最多放6个。可以从1到6构造6个抽屉,则问题转化为至少有几个含小球数目相同的盒子在同一个抽屉里。因为共有18个盒子.18+6:3。故假设每个抽屉里有3个盒子的小球数目是相同的,故18个盒子里放的小球最多有3×(1+2+3+4+5+6)=63
