黑板上写着8，9，10，11，12，13，14七个数，每次任意擦去两个数，再写上这两个数的和减1。例如，擦掉9和13，要写上21。经过几次后，黑板上就会只剩下一个数，这个数是多少? A．67 B．71 C．73 D．79

题目

黑板上写着8，9，10，11，12，13，14七个数，每次任意擦去两个数，再写上这两个数的和减1。例如，擦掉9和13，要写上21。经过几次后，黑板上就会只剩下一个数，这个数是多少? A．67 B．71 C．73 D．79

相似考题

1.从1、2、3、4、5、6、7、8、9、10这10个数字中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积?（ ）A．13B．14C． 18D． 20

2.：从1，3，9，27，81，243这六个数中，每次取出若干个数(每次取数，每个数只能取一次)求和，可以得到一个新数，一共有63个数。如果把它们以小到大依次排列起来是：1，3，4，9，10，12，…那么，第60个数是（ ）。A．220B．380C．360D．410

3.任意两个数的最小公倍数一定大于这两个数中的任何一个数。()此题为判断题(对，错)。

4.把100分成两个数的和，使第一个数加3，与第二个数减3的结果相等，这两个数分别是多少？

更多“黑板上写着8,9,10,11,12,13,14七个数,每次任意擦去两个数,再写上这两个数的和减1。例如,擦掉9和13 ”相关问题

  • 第1题：

    从1，2，3，……，50这五十个数中，取出若干个数，使其中任意两个数的和都不能被7整除，则最多能取多少个数( )。

    A. 21    B. 22C. 23   D. 29


    从0开始，每7个数一组（0——6，7——13，......，42——48，共七组）中，最多可以选4个数（分别是除7余0，1，2，3的数）
    所以，它们之中可以选7*4＝28个数。
    另外：0不包含在其中，要减去1个数；49和50两个数除7的余数分别是0和1，也要计算上，再加2个数。
    故，最多共可取28－1+2＝29个数

  • 第2题：

    从1、2、3、4、5、6、7、8、9、10这10个数中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不l司的乘积？（ ）

    A．13

    B．14

    C．18

    D．20


    正确答案：A
    从整体考虑分两组，和不变：1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55，最接近的两组为27+28，所以共有27-15+1=13个不同的积。

  • 第3题：

    黑板上写着8，9，10，11，12，13，14七个数，每次任意擦去两个数，再写上这两个数的和减10例如，擦掉9和13，要写上21。经过几次后，黑板上就会只剩下一个数，这个数是多少?

    A．67

    B．71

    C．73

    D．79


    正确答案：B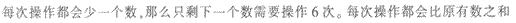

  • 第4题：

    从1，3，9，27，8l，243这六个数中，每次取出若干个数(每次取数，每个数只能取一次)求和、可以得到一个新数，一共有63个数。如果把它们以小到大依次排列起来是：1，3，4，9，10，12，…。那么，第60个数是（ ）

    A. 220
    B. 380
    C. 360
    D. 410

    答案：C
    解析：
    一共63个数，第60个也就是倒数第四个，从大往小排列的第四个数。即364-4=360。故答案为C。

  • 第5题：

    以下命题中正确的一个是（）。

    • A、两个数的和为正数，则这两个数都是正数
    • B、两个数的差为负数，则这两个数都是负数
    • C、两个数中较大的一个绝对值也较大
    • D、加上一个负数，等于减去这个数的绝对值
    • E、一个数的2倍大于这个数本身

    正确答案:D

  • 第6题：

    数据结构与算法里，完数N的因子一定包括1和N-1这两个数。


    正确答案:错误

  • 第7题：

    韩国人崇拜熊、虎，忌讳“4”和“13”这两个数字。（）


    正确答案:正确

  • 第8题：

    黑板上写有一串数字：1、2.3、……、2011、2012，任意擦去几个数，并写上被擦去的几个数的和被11除所得的余数，这样操作下去，一直到黑板上只剩下一个数，则这个数是（）

    • A、0
    • B、1
    • C、2
    • D、4

    正确答案:A

  • 第9题：

    单选题
    对于下面两个问题：（1）从5，11，13三个数中每次取出两个数相加，最多可以得出多少个和?（2）从5，11，13三个数中每次取出两个数相减，最多可以得出多少个差?可以得出（　　）．
    A

    问题（1），（2）都属于排列问题

    B

    问题（1），（2）都属于组合问题

    C

    问题（1）属于排列问题，问题（2）属于组合问题

    D

    问题（1）属于组合问题，问题（2）属于排列问题


    正确答案： D
    解析：
    与顺序有关就属于排列，与顺序无关就属于组合．

  • 第10题：

    单选题
    一个正方体木块放在桌子上，每一面都有一个数，位于相对面两个数的和都等于13，小张能看到顶面和两个侧面，看到的三个数和为18；小李能看到顶面和另外两个侧面，看到的三个数的和为24，那么贴着桌子的这一面的数是多少？（　　）
    A

    4

    B

    5

    C

    6

    D

    7


    正确答案： A
    解析：
    将小张与小王看到的面合在一起，则实际共看到2个顶面与4个不同的侧面。而四个不同侧面恰为两组对面，即其数字之和为13×2＝26。则顶面的数字为（18＋24－26）÷2＝8，因此底面数字为13－8＝5。

  • 第11题：

    黑板上写着8、9、10、11、12、13、14七个数，每次任意擦去两个数，再写上这两个数的和减1。例如，擦掉9和13，要写上21。经过几次后，黑板上就会只剩下一个数，这个数是多少?

    A．67

    B．71

    C．73

    D．79


    正确答案：B
    [答案] B[解析]所剩之数等于原来的七个数之和减6，故这个数是(8+9+10+11+12+13+14)-6=71。

  • 第12题：

    从1、2、3、4、5、6、7、8、9、10这10个数中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积？( )

    A．13

    B．14

    C．18

    D．20


    正确答案：A
    A【解析】从整体考虑分两组，和不变：1+2+3+4+5+6+7+8+9+10=55，从极端考虑分成最小和最大的两组为(1+2+3+4+5)+（6+7+8+9+10）=15+40=55，最接近的两组为27+28，所以共有27-15+1=13个不同的积。

  • 第13题：

    有4个不同的自然数，它们当中任意两数的和是2的倍数；任意3个数的和是3的倍数，为了使得这4个数的和尽可能小，则这四个数的和为（ ）。

    A. 40
    B. 42
    C. 46
    D. 51

    答案：A
    解析：
    任意两个数的和是2的倍数，所以这些数的奇偶性相同。任意三个数的和是3的倍数，所以这些数除以3，所得余数必定相同（否则在三个数的和中换一个数，和将不是3的倍数）。于是， 这些数除以6所得余数相同，故这最小的四个数为1，7，13，19。所以这四个数的和为1 + 7 + 13 + 19 = 40。

  • 第14题：

    从1、3、9、27、81、243这六个数中，每次取出若干个数(每次取数，每个数只能取一次)求和，可以得到一个新数，一共有63个数。如果把它们以小到大依次排列起来是：
    1，3，4，9，10，12，…。那么，第60个数是（　　）。

    A.363
    B.361
    C.360
    D.355

    答案：C
    解析：
    由题目可知，第63个数是364(即6个数之和)，第62个数是364-1=363，第61个数是364-3=361，第60个数是364-1-3=360。

  • 第15题：

    在1和2015之间（包括1和2015在内）不能被4、5、6三个数任意一个数整除的数有（）个。


    正确答案:1075

  • 第16题：

    给法国妇女送花时，宜送单数，但要避开“1”与“13”这两个数目。


    正确答案:正确

  • 第17题：

    两个自然数，它们倒数的和是1/2，这两个数是（）

    • A、0和2
    • B、1和1
    • C、4和2
    • D、3和6

    正确答案:D

  • 第18题：

    填空题
    在1和2015之间（包括1和2015在内）不能被4、5、6三个数任意一个数整除的数有（）个。

    正确答案： 1075
    解析： 暂无解析

  • 第19题：

    单选题
    有4个不同的自然数，他们当中任意两数的和是2的倍数，任意3个数的和是3的倍数，为了使这4个数的和尽可能小，则这4个数的和为（）
    A

    40

    B

    42

    C

    46

    D

    51


    正确答案： D
    解析： 暂无解析

相关内容