一条执行考察任务的科考船,现从8地沿河驶向人海口,已知B地距人海口60千米,水速为每小时6千米,若船顺流而下,则用4小时可以到达人海口,该船完成任务从人海口返回并按原速度航行4小时后,由于海水涨潮,水流方向逆转,水速变为每小时3千米,则该船到达B地还需再航行多少小时? A.5 B.4 C.3 D.2
题目
一条执行考察任务的科考船,现从8地沿河驶向人海口,已知B地距人海口60千米,水速为每小时6千米,若船顺流而下,则用4小时可以到达人海口,该船完成任务从人海口返回并按原速度航行4小时后,由于海水涨潮,水流方向逆转,水速变为每小时3千米,则该船到达B地还需再航行多少小时? A.5 B.4 C.3 D.2
相似考题
更多“一条执行考察任务的科考船,现从8地沿河驶向人海口,已知B地距人海口60千米,水速为每小时6千米,若船顺流而下,则用4小时可以到达人海口,该船完成任务从人海口返回并按原速度航行4小时后,由于海水涨潮,水流方向逆转,水速变为每小时3千米,则该船到达B地还需再航行多少小时? A.5 B.4 C.3 D.2”相关问题
-
第1题:
:旅游船顺水速度每小时8千米,逆水速度每小时7千米,两船同时同地出发,甲船顺水而下然后返回,乙逆水而上然后返回,经过2小时同时回到出发地点,在这2小时中有多少时间两船航行方向相同?( )
A.2/15小时
B.1/5小时
C.4/15小时
D.1/3小时
正确答案:A
-
第2题:
甲、乙两只船在同一条河中以相同的静水速前进,已知静水速为水流速的三倍,且两 只船上都配备了船帆, 扬起后可增速 15 米/秒。 现两只船位于同一直线的两个码头相向而 行,甲船扬起船帆且顺风顺水,行驶 3.9 小时后两船相遇。 后两船掉头按原线路返回,甲船忘 记收起船帆而乙船忘记扬起船帆,同线路行驶 6.5 小时后分别到达原来码头。问静水速为多 少米/秒
A.50
B.30
C.15
D.10答案:B解析:根据题意,设水流速度为v,静水速度为3v,则根据题意可列式3.9(4v+15+2v)=6.5(2v-15+4v),解得v=10,因此静水速度是30米/秒。 -
第3题:
—只装有动力桨的船,其单靠人工划船顺流而下的速度是水速的3倍。现该船靠人工划动从A地顺流到达B地,原路返回时只开足动力桨行驶,用时比来时少2/5。问船在静水中开足动力浆行驶的速度是人工划船速度的多少倍?()
A. 2 B. 3 C. 4 D. 5答案:B解析:设水速是1,则顺水速度为3,人工划船静水速度=3-1 = 2。
顺水时间:逆水时间=1 : (1-2/5),则顺水速度:逆水速度=3 : 5。
所以动力浆逆水行驶时速度为5,动力浆静水速度=5 + 1= 6,因此所求比例为6 : 2=3 : 1。 -
第4题:
—条河的水流速度为每小时4公里。一条船以恒定的速度逆流航行6公里后,再返回 原地,共耗时2小时(不计船掉头的时间)。请问船逆流航行与顺流航行的速度之比是多少?A.1:3
B.2:3
C.1:2
D.1:4答案:A解析:
-
第5题:
一只装有动力桨的船,其单靠人工划船顺流而下的速度是水速的3倍。现该船靠人工划 动从A地顺流到达B地,原路返回时只开足动力桨行驶,用时比来时少2/5。问船在静水 中开足动力浆行驶的速度是人工划船速度的多少倍?( )A. 2
B. 3
C. 4
D. 5答案:B解析:
-
第6题:
甲、乙两船同时从A地出发,甲船逆流前往B地,乙船顺流前往C地,1小时后两艘船同时掉头航向A地,甲船比乙船早1小时返回,已知甲船的静水速度是水流的3倍,那么甲船的静水速度和乙船的静水速度之比是:A. 3:5
B. 2:3
C. 3:4
D. 2:5答案:A解析:
-
第7题:
单选题某船由甲地驶向乙地,逆水而行,若船速每小时8公里,3小时可到达;船速每小时5公里,5.25小时可到达。若船速为每小时6公里,则()小时可到达。A4
B4.2
C4.6
D5
正确答案: D解析: 路程一定,速度和时间成反比。时间比为3∶5.25=4∶7,速度比为7∶4,显然水流的速度为1公里/小时。把船速为8公里/小时和6公里/小时的情况进行正反比关系,速度比为7∶5,时间比为5∶7=3∶4.2,故选B。 -
第8题:
一条执行考察任务的科考船,现从8地沿河驶人海口,已知B地距入海口60千米,水速为每小时6千米。若船顺流而下,则用4小时可以到达人海口,该船完成任务从人海口返回并按原速度航行4小时后。由于海水涨潮,水流方向发生变化,水速变为每小时3千米,则该船到达B地还需再航行( )小时。A.5
B.4
C.3
D.2答案:B解析:从B地到入海口总路程为60千米,水速为6千米/小时。因为船顺流而下到达人海口用时4小时,所以船速为60÷4-6=9千米/小时。从人海口返回,逆流航行4小时,该船行驶的路程为(9-6)x4=12千米。此时水流方向发生变化,逆流改为顺流,且水速变为3千米/小时,则剩余路程用时(60-12)÷(9+3)=4小时。 -
第9题:
—条执行考察任务的科考船,现从B地沿河驶向入海口,已知B地距入海口 60千米,水速为每小时6千米,若船顺流而下,则用4小时可以到达入海口,该船完成任务从入海口返回并按原速度航行4小时后,由于海水涨潮,水流方向逆转,水速变为每小时3千米,则该船到达B地还需再航行多少小时?A.5
B.4
C.3
D.2答案:B解析:此题为流水问题。路程为60千米,水速为6千米/小时,因为船顺流而下到达入海口用时 4小时,所以船速为60÷4-6=9千米/小时。逆流航行4小时,该船行驶的路程为(9-6)×4=12千米,此时水流方向逆转,且水速变为3千米/小时,则剩余路程用时(60-12)÷(9+3)=4小时。 -
第10题:
一条河的水流速度为每小时4公里。一条船以恒定的速度逆流航行6公里后,再返回原地,共耗时2小时(不计船掉头的时间)。请问船逆流航行与顺流航行的速度之比是多少?( )
A1∶3
B2∶3
C1∶2
D1∶4答案:A解析:设船速为,则根据已知有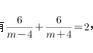 ,解之得m=8,所以船逆流航行与顺流航行的速度之比为
,解之得m=8,所以船逆流航行与顺流航行的速度之比为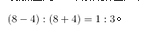 。
。
故正确答案为A。 -
第11题:
—条河的水流速度为每小时4公里。一条船以恒定的速度逆流航行6公里后,再返回原 地,共耗时2小时(不计船掉头的时间)。请问船逆流航行与顺流航行的速度之比是多少?A.l:3
B.2:3
C.l:2
D.l:4答案:A解析:
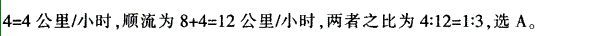
-
第12题:
—条执行考察任务的科考船,现从B地沿河驶向人海口,巳知B地距入海口60千米,水速为每小时6千米,若船顺流而下,则用4小时可以到达入海口,该船完成任务从人海口返回并按原速度航行4小时后,由于海水涨潮,水流方向逆转,水速变为每小时3千米,则该船到达B地还需再航行多少小时?A.5
B.4
C.3
D.2答案:B解析:路程为60千米,水速为6千米/小时,因为船顺流而下到达人海口用时4小时,所以船速为60÷4-6=9千米/小时。逆流航行4小时,该船行驶的路程为(9-6)x4=12千米,此时水流方向逆转,且水速变为3千米/小时,则剩余路程用时(60-12)÷(9+3)=4小时。 -
第13题:
某船由甲地驶向乙地,逆水而行,若船速每小时8公里,3小时可到达;船速每小时5公里,5.25小时可到达。若船速为每小时6公里,则()小时可到达。
- A、4
- B、4.2
- C、4.6
- D、5
正确答案:B -
第14题:
问答题一艘轮船从甲港顺水航行到已港,立即逆水返航到甲港,共用8小时,已知轮船顺水速度比逆水速度每小时快20千米,又知前4小时比后4小时多航行60千米,问两地路程?正确答案: 设顺水速度为v,则逆水速度为v-20,从甲港到乙港用了h个小时,从乙港到甲港用了8-h个小时,两地路程为s,则:
s/v+s/(v-20)=8(1)
s/v=h(2)
s/(v-20)=8-h(3)
hv+(4-h)(v-20)-4(v-20)=60(4)
由上述4式可得v=50,h=3,s=150.
故两地之间的路程为150千米解析: 暂无解析
