甲、乙二人同时从A地去B地，甲每分钟行60米，乙每分钟行90米，乙到达B地后立即返回，并与甲相遇，相遇时，甲还需行3分钟才能到达B地，问A、B两地相距多少米?（ ） A．1 350米 B．1 080米 C．900米 D．720米

题目

甲、乙二人同时从A地去B地，甲每分钟行60米，乙每分钟行90米，乙到达B地后立即返回，并与甲相遇，相遇时，甲还需行3分钟才能到达B地，问A、B两地相距多少米?（ ） A．1 350米 B．1 080米 C．900米 D．720米

相似考题

1.：甲、乙两车同时从A地出发开往B地。甲车到达8地后立即返回，在离B地45千米处与乙车相遇，甲、乙两车的速度比是3：2。求A，B两地的路程是多少千米？（ ）A．220B．200C．225D．250

2.甲、乙二人分别从A、B两地同时相向而行，甲的速度是乙的1.5倍，二人相遇后继续行进，甲到B地、乙到A地后立即返回。已知二人第四次相遇的地点距离第三次相遇的地点20千米，那么A、B两地相距多少千米?A．50B．40C．30D．25

3.甲、乙两车同时从A、B两地出发，相向而行。甲到达B地后立即返回，回到A地后又立即向B地行驶；乙到达A地后立即返回，回到B地后又立即向A地行驶。两车如此往复，行驶速度不变。若两车第2次迎面相遇距B地20千米，第3次迎面相遇距离A地10千米，问A、B两地的距离是多少千米？（ ）A.20B.30C.40D.70

4.甲、乙两船分别在一条河的A、B两地同时相向而行，甲顺流而下，乙逆流而行。相遇时，甲、乙两船的航程相等，此后继续前进，甲到达B地，乙到达A地后，都立即按原来路线返航，两船第二次相遇时，甲船比乙船少行1千米。如果第一次相遇到第二次相遇时间相隔1小时20分． 问河水的流速是每小时多少千米? A．0.375 B．0.5 C．0.75 D．1.5

更多“甲、乙二人同时从A地去B地,甲每分钟行60米,乙每分钟行90米,乙到达B地后立即返回,并与甲相遇,相遇 ”相关问题

  • 第1题：

    甲、乙二人从A、B两地同时出发相向而行，甲每分钟行80米，乙每分钟行60米，出发一段时间后，二人在距中点120米处相遇，如果甲出发后在途中某地停留一会儿，二人还将在距中点120米处相遇。问甲在途中停留了多少分钟？

    A.7B.8C.9D.10


    解：∵二人在距中点120米处相遇，
    ∴一人比一人多走了120×2=240(米)
    第一次明显甲多走了，所花时间为：240÷(80-60)=12(分钟)。
    A，B两地的距离为12×(60+80)=1680(米)
    第二次是乙多走了，设所花时间为t分钟，则：
    60t乙=1/2×1680+120  —— 解得t乙=16
    80t甲=1/2×1680-120  —— 解得t甲=9
    甲在途中停留了16-9=7(分钟)。

  • 第2题：

    A、B两地相距540千米。甲、乙两车同时从A地出发，往返行驶于A、B两地之间，都是到达之后立即返回，乙车较甲车快。设两辆车同时从A地出发后第一次和第二次相遇都在途中P地。那么到两车第三次相遇为止，乙车共走了多少千米？

    A．1080

    B．1620

    C．1890

    D．2160


    正确答案：D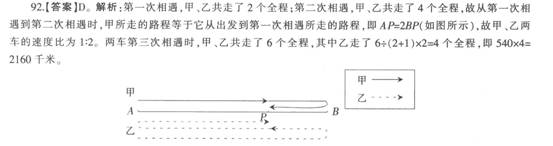

  • 第3题：

    两辆电动小汽车在周长为360米的圆形道上不断行驶，甲车每分钟速度是20米。甲、乙两车同时分别从相距90米的A、B两点相背而行，相遇后乙车立即返回，当它到达B点时，甲车过B点，又回到A点，此时甲车立即返回。问再过多少分钟能与乙车相遇?（ ）

    A．2

    B．3

    C．4

    D．5


    正确答案：B
    如右图，设第一次甲车与乙车相遇点是C点，则乙在BC弧上往返一次所需时间就是甲车行驶圆形道一圈所需时间：360÷20=18(分钟)。它们自出发点至C点，各自行驶了18÷2=9(分钟)。从B顺时针到C路程是360-90-20×9=90(米)。乙车速度是每分钟90÷9=10(米)，则所求时间90÷(20+10)=3(分钟)。故本题正确答案为B。

  • 第4题：

    ：甲、乙两车同时从A、B两地相向而行，在距B地54千米处相遇，它们各自到达对方车站后立即返回，在距A地42千米处相遇。问A、B两地相距多少千米?(提示：相遇时它们行了3个全程)（ ）。

    A．120

    B．150

    C．180

    D．200


    正确答案：A

    本题考查的是相遇问题。设A、B两地相距s千米，令甲的速度是x千米/小时，乙的速度为y千米/4,时。
        两车同时从A、B两地相向而行，在距B地54千米处相遇时，
        根据他们相遇的时间相等得：(s一54)/x=54/y………………①
        再次相遇时，甲乙所用时间同样是相等的，则：
        (s-54+42)/y=(54+S一42)/x………………………………②
        由①、②整理可得S2—120s一0
        解之得Sl一o(不合题意舍去)娩一l20
        故A、B两地相距l20千米。答案选A。

  • 第5题：

    AB两地间有条公路，甲从A地出发步行到B地，乙骑摩托车从B地不停的往返两地之间，若它们同时出发，80分钟后两人第一次相遇，100分钟后乙第一次超过甲，当甲到达B地时，甲乙相遇（ ）次。


    A.5
    B.7
    C.9
    D.10

    答案：A
    解析：

    个全程 ， 第一次是相遇 ， 第二次是追上 ， 所以 ，共相遇5次， 追上4次

  • 第6题：

    甲、乙二人分别从A、B两地驾车同时出发，匀速相向而行，甲车的速度是乙车的2/3，两车开出6小时后相遇，相遇后以原速继续前进。问甲比乙晚几个小时到达目的地？

    A. 2
    B. 3
    C. 4
    D. 5

    答案：D
    解析：
    甲乙二人的速度比是2:3，所以时间比就是3:2，根据时间的比例，甲剩下的路程所需时间是9h，乙剩下的路程时间是4h，二者加上原来的时间就是15h和10h，所以选择D。

  • 第7题：

    甲、乙、丙三人，甲每分钟走50米，乙每分钟走40米，丙每分钟走35米，甲、乙从A地，丙从B地同时出发，相向而行，丙遇到甲2分钟后遇到乙，那么，A、B两地相距多少米？

    A250 米
    B500 米
    C750 米
    D1275 米


    答案：D
    解析：

  • 第8题：

    上午8点甲、乙二人同时从A地出发前往B地，甲骑电动车、乙步行。40分钟后甲到达B地，此时乙距离两地的中点处还需走10分钟，于是乙停下来等待甲返回接他，若甲立刻原速返回，当甲到达乙处接上乙立刻前往B地，速度保持不变。则甲、乙到达B地时甲共骑行（ ）分钟。

    A.88
    B.44
    C.80
    D.94

    答案：A
    解析：
    第一步，本题考查行程问题，属于相遇追及类。
    第二步，甲行驶全程需40分钟；乙走40分钟距离中点处还需10分钟，则乙走全程需（40＋10）×2＝100（分钟），甲、乙速度比为100∶40＝5∶2。
    第三步，乙停下来的位置距离中点还需走10分钟，则甲返回接乙需行驶20＋10×



    ＝24（分钟），接到乙后行驶至B地还需24分钟。
    第四步，甲、乙均到达B地合计需要40＋24＋24＝88（分钟）。

    因此，选择A选项。

  • 第9题：

    上午8点甲、乙二人同时从A.地出发前往B地，甲骑电动车，乙步行。40分钟后甲到达B.地，此时乙距离两地的中点处还需走10分钟，于是乙停下来等待甲返回接他。若甲立刻原速返回，当甲到达乙处接上乙立刻前往B地，速度保持不变。则甲、乙到达B地时甲共骑行（ ）分钟。

    A.88
    B.44
    C.80
    D.94

    答案：A
    解析：

  • 第10题：

    甲、乙两人分别从A、B两地同时同向沿着笔直的公路出发去往C地，并且到了C地立即返回。已知B地在A地前方4000米，A、B两地的距离是

    A、C两地距离的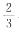，甲骑车每 分钟走250米，乙步行每分钟走100米，那么甲、乙两人相遇时距C地多少米？（ ）

    答案：B
    解析：
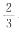    A、C两地距离为4000 ÷ = 6000（米），则B、C两地的距离为2000米，甲骑车从A地到C地需6000 ÷ 250 = 24（分），乙步行从B地到C地需2000÷100 = 20（分），那么 20分钟后乙从C地返回，甲此时距C地距离为6000 —250×20 = 1000（米）。此时问题便转化为两人的相遇问题，相遇时距C地距离为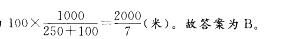

  • 第11题：

    甲、乙二人分别同时从A、B两地出发相向匀速而行，两人相遇之后，甲又经过了2个小时到达B地；乙又经过4个半小时到达A地，若他们到达后都立即调头，当他们再次相遇时，距他们第一次相遇经过了多少个小时？(）

    A.5
    B.5.5
    C.6
    D.6.5

    答案：C
    解析：

  • 第12题：

    单选题
    甲、乙二人分别同时从A、B两地出发相向匀速而行，两人相遇之后，甲又经过了2个小时到达B地；乙又经过4个半小时到达A地；若他们到达后都立即掉头，当他们再次相遇时，距他们第一次相遇经过了多少个小时（）
    A

    5

    B

    5.5

    C

    6

    D

    6.5


    正确答案： C
    解析： 设从出发到第一次相遇时间为t，由题意可知，相同的路程，甲走t小时，乙需要走4.5小时；甲走2小时，乙需要走t小时，则t/4.5=2/t，得t=3。根据直线多次相遇的结论，从第一次相遇到第二次相遇经过的时间等于第一次相遇所用时间的2倍，为6小时。

  • 第13题：

    甲、乙、丙三人，甲每分钟走 50 米，乙每分钟走 40 米，丙每分钟走 35米，甲、乙从

    A 地，丙从 B 地同时出发，相向而行，丙遇到甲 2 分钟后遇到乙，那么，A、B 两地相距多

    少米？( )

    A.250 米

    B.500 米

    C.750 米

    D.1275 米


    正确答案：D

  • 第14题：

    甲从A地，乙和丙从B地同时出发，相向而行。已知甲每小时行65公里，乙每小时行73公里，丙每小时行55公里。甲和乙相遇后，经过15小时又与丙相遇，那么A、B两地相距( )公里。

    A．10100

    B．13800

    C．10600

    D．14800


    正确答案：B

  • 第15题：

    甲、乙二人分别从A．B两地同时相向而行，乙的速度是甲的3/4，二人相遇后继续前进，甲到B地、乙到A地后立即返回．已知二人第二次相遇的地点与第一次相遇的地点相距2千米，那么A、B两地相距多少千米？( )

    A．5

    B．7

    C．9

    D．11


    正确答案：B
    B[解析]设A、B相距S千米，根据题意，第一次相遇时甲走了（4/7）S千米，乙走了（3/7）S千米；第二次相遇时甲走了[S+（3/7）S+2]千米，乙走了[S+（4/7）S-2]千米，则3/4[S+（3/7）S+2]=[S+（4/7）S-2]，解得S=7。故A、B相距7千米。

  • 第16题：

    甲、乙两船分别在一条河的A，B两地同时相向而行，甲顺流而下，乙逆流而上。相遇时，甲乙两船行了相等的航程，相遇后继续前进，甲到达B地、乙到达A地后,都立即按原来路线返航，两船第二次相遇时，甲船比乙船少行1000米。如果从第一次相遇到第二次相遇的时间相隔为1小时20分，那么河水的流速是多少？

    A.0.375千米/小时
    B.0.500千米/小时
    C.0.750千米/小时
    D.0.910千米/小时

    答案：A
    解析：
    因为甲、乙第一次相遇时行驶的路程相等，所以有甲、乙同时刻各自到达B、A两地。则有甲静水速度+水速=乙静水速度-水速。
    甲乙返航时，甲在河流中行驶的速度为（甲静水速度－水速），乙在河流中的速度为（乙静水速度+水速）。它们的速度差为4倍水速。
    从第一次相遇到第二次相遇，两船共行驶了AB路程的2倍，而从返航到第二次相遇两船共行驶了AB的路程，需要80÷2=40分钟。所以4倍水速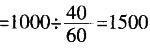米/小时，水速=375米/小时=0.375千米/小时。

  • 第17题：

    甲、乙两人同时从A地去B地,甲每分钟行60米,乙每分钟行90米,乙到达B地后立即返回,并与甲相遇,相遇时,甲还需行3分钟才能到达B地,问A,B两地相距多少米?


    A. 1350米
    B. 1080米
    C. 900米
    D. 720米

    答案：C
    解析：
    解题指导： 设两地距离为X，相遇时甲还有三分钟到达B地，则甲与B地相距3*60=180米，甲走的路程为：X-180，乙走的路程为X+180，相遇时两人所花时间相同，即（X-180）/60=（X+180）/90，X=900。故答案为C。

  • 第18题：

    甲、乙两人骑自行车从东西两地同时出发，相向而行，经过8分钟相遇。如果甲每分钟少行180米，而乙每分钟多行230米，经过7分钟就能相遇，东西两地相距多少米?()

    A. 1240
    B. 1440
    C. 1840
    D. 2800

    答案：D
    解析：
    设东西两地距离为S，甲乙二人速度分别是X米/分钟和Y米/分钟，根据题意列方程式为S=（X+Y)*8=（x+y+50)*7，可解得X+Y=350，S=2800。故答案为D。

  • 第19题：

    甲、乙二人绕着圆形操场跑道散步，甲顺时针走，乙逆时针走，两人在跑道A处同时出发，甲每分钟走90米，乙每分钟走60米，当甲、乙两人在跑道B处相遇时，乙加快了速度，甲在原地停留4分钟后保持原来的速度继续往前走，最后甲、乙二人仍在A处相遇。已知该操场的周长为1800米，那么相遇后，乙的速度变为每分钟（ ）米。

    A.70
    B.80
    C.90
    D.100

    答案：C
    解析：
    第一步，本题考查行程问题。
    第二步，甲、乙在B处相遇，根据S=（+）×t代入数据：1800=（90+60）×t，解得t=12（分钟），则甲走了90×12=1080米，乙走了60×12=720米。
    第三步，要回到A处：甲要再走720米，用时720÷90=8分钟，加上原地停留的4分钟，共用时8+4=12分钟，故乙加速后再走1080米也需用时12分钟，加速后的速度为每分钟1080÷12=90米。

  • 第20题：

    甲、乙二人分别从A、B两地同时出发，相向而行，甲的速度是乙的4倍，甲用时15分钟到达B地后立即返回，甲乙第二次相遇后，乙再走（ ）分钟才能到达A地。

    A.40
    B.30
    C.45
    D.33.3

    答案：A
    解析：

  • 第21题：

    如下图，A、C两地相距2千米，C、B两地相距5千米。甲、乙两人同时从C地出发，甲向B地走，到达B地后立即返回；乙向A地走，到达A地后立即返回。如果甲速度是乙速度的1.5倍，那么在乙到达D地时，还未能与甲相遇，他们还相距0.5千米，这时甲距C地多少千米？（ ）

    A. 1.4 B. 1.9 C. 2.3 D. 3.3


    答案：B
    解析：
    由甲速是乙速的1.5倍，可知甲所走路程是乙所走路程的1.5倍。设C、D距离为x 千米，则乙走的路程是(4+x)千米，甲所走路程为(4+x)X1. 5千米，根据题意有(4+x)X1.5 = 5X2-x-0. 5，解得：x=1.4，此时甲距C地1. 4 + 0. 5 = 1. 9(千米)，本题正确答案为B。

  • 第22题：

    甲、乙两货车同时从相距300千米的A、B两地相对开出，甲车以每小时60千米的速度开往B地，乙车以每小时40千米的速度开往A地，甲车到达B地停留2小时后以原速返回，乙车到达A地停留半小时后以原速返回。那么，返回时两车相遇地点与A地相距____千米。

    A. 60
    B. 84
    C. 96
    D. 110

    答案：C
    解析：
    甲车从A地到达B地行驶及等待的时间为300÷60+2=7（小时）；乙车从A地到达B地行驶及等待的时间为300÷40+0.5=8（小时）。即甲车从B地先行8-7=1（小时）。因此，甲车从B地先行1小时后（走60千米），乙车才从A地出发．所以，两车返回时的相遇时间是（300-60）÷（60+40）=2.4（小时）。故两车返回时相遇地点与A城相距40×2.4=96（千米）。所以选C。

  • 第23题：

    单选题
    A、B两地相距540千米。甲、乙两车往返行驶于A、B两地之间，都是到达一地之后立即返回，乙车较甲车快。设两辆车同时从A地出发后第一次和第二次相遇都在途中P地。那么两车第三次相遇为止，乙车共走了多少千米？（）
    A

    120

    B

    1440

    C

    2160

    D

    2880


    正确答案： D
    解析： 暂无解析

相关内容