某算法的时间复杂度可用递归式[*],表示，若用[*]表示该算法的渐进时间复杂度的紧致界，则正确的是(62)。A．(nlg2n)B．(nlgn)C．(n2)D．(n3)
题目
某算法的时间复杂度可用递归式[*],表示，若用[*]表示该算法的渐进时间复杂度的紧致界，则正确的是(62)。
A．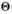
(nlg2n)
B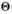．(nlgn)
C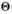．(n2)
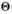D．(n3)
相似考题
参考答案和解析
正确答案：A
解析：本题利用递归树方法求解。得到的递归树如下图所示：
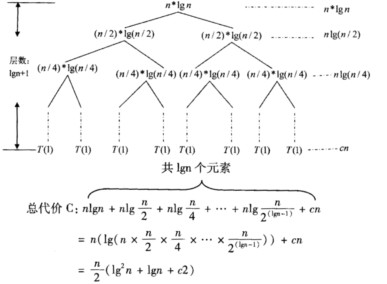
由于C属于O(nlg2n)且C属于Ω(nlg2n)，所以总的时间复杂度为A。
解析：本题利用递归树方法求解。得到的递归树如下图所示：
由于C属于O(nlg2n)且C属于Ω(nlg2n)，所以总的时间复杂度为A。
更多“ 某算法的时间复杂度可用递归式[*],表示，若用[*]表示该算法的渐进时间复杂度的紧致界，则正确的是(62)。A．(nlg2n)B．(nlgn)C．(n2)D．(n3) ”相关问题
-
第1题：
在某个算法时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为（ ），若问题的规模增加了16倍，则运行时间增加（ ）倍。
A.Θ(n) B.Θ(nlgn) C.Θ(n2) D.Θ(n2lgn) A.16 B.64 C.256 D.1024
正确答案：C,C
-
第2题：
已知算法A的运行时间函数为T（n）=8T（n/2）+n2，其中n表示问题的规模，则该算法的时间复杂度为（ ）A.θ（n）
B.θ（nlgn）
C.θ（n2）
D.θ（n3）答案：D解析：本题需要用到特定形式的递归式分析法：
在本题中，a=8,b=2，故符合（1）的情况。时间复杂度为：O（n3）。a=16,b=4 -
第3题：
某个算法的时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为（62），若问题的规模增加了16倍，则运行时间增加（63）倍。A.O(n)
B.O(nlgn)
C.O(n2)
D.O(n2lgn)答案：C解析：对于递归式，假设T(1)=1，则：
T(n)=T(n-1)+n
=T(n-2)+n-1+n
=T(n-3)+n-2+n-1+n
=1+2+…+n-1+n
=n(n+1)/2
可见，时间复杂度为O(n2)。若问题的规模增加了16倍，则运行时间增加了162=256倍。 -
第4题：
某个算法的时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为 （请作答此空） ，若问题的规模增加了16倍，则运行时间增加 （ ） 倍。A.O(n)
B.O(nlgn)
C.O(n2)
D.O(n2lgn)答案：C解析：对于递归式，假设T(1)=1，则：
T(n)=T(n-1)+n
=T(n-2)+n-1+n
=T(n-3)+n-2+n-1+n
=1+2+…+n-1+n
=n(n+1)/2
可见，时间复杂度为O(n2)。若问题的规模增加了16倍，则运行时间增加了162=256倍。 -
第5题：
某个算法的时间复杂度递归式T（n）=T（n-1）+n，其中n为问题的规模，则该算法的渐进时间复杂度为（请作答此空），若问题的规模增加了16倍，则运行时间增加（ ）倍。A.O（n）
B.O（nlgn）
C.O（n2）
D.O（n2lgn）答案：C解析：对于递归式，假设T（1）=1，则：T（n）=T（n-1）+n=T（n-2）+n-1+n=T（n-3）+n-2+n-1+n=1+2+…+n-1+n=n（n+1）/2可见，时间复杂度为O（n2）。若问题的规模增加了16倍，则运行时间增加了162=256倍。