设32位浮点数格式如下。以下关于浮点数表示的叙述中，正确的是（请作答此空）。若阶码采用补码表示，为8位（含1位阶符），尾数采用原码表示，为24位（含1位数符），不考虑规格化，阶码的最大值为（ ）。 A.浮点数的精度取决于尾数M的位数，范围取决于阶码E的位数 B.浮点数的精度取决于阶码E的位数，范围取决于尾数M的位数 C.浮点数的精度和范围都取决于尾数M的位数，与阶码E的位数无关 D.浮点数的精度和范围都取决于阶码E的位数，与尾数M的位数无关

题目
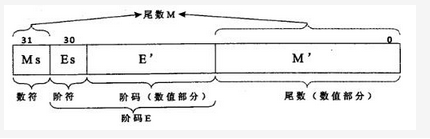
设32位浮点数格式如下。以下关于浮点数表示的叙述中，正确的是（请作答此空）。若阶码采用补码表示，为8位（含1位阶符），尾数采用原码表示，为24位（含1位数符），不考虑规格化，阶码的最大值为（ ）。

A.浮点数的精度取决于尾数M的位数，范围取决于阶码E的位数
B.浮点数的精度取决于阶码E的位数，范围取决于尾数M的位数
C.浮点数的精度和范围都取决于尾数M的位数，与阶码E的位数无关
D.浮点数的精度和范围都取决于阶码E的位数，与尾数M的位数无关
相似考题

1.● 浮点数的一般表示形式为N＝2E×F，其中E为阶码，F为尾数。以下关于浮点表示的叙述中，错误的是（3）。两个浮点数进行相加运算，应首先（4）。（3）A. 阶码的长度决定浮点表示的范围，尾数的长度决定浮点表示的精度B. 工业标准IEEE754浮点数格式中阶码采用移码、尾数采用原码表示C. 规格化指的是阶码采用移码、尾数采用补码D. 规格化表示要求将尾数的绝对值限定在区间[0.5, 1)（4）A. 将较大的数进行规格化处理B. 将较小的数进行规格化处理C. 将这两个数的尾数相加D. 统一这两个数的阶码

2.在某字长为8的机器中浮点数的格式为：阶符1位，阶码2位(补码)，尾符1位，尾数4位(原码)，-0.000875的规格化浮点数为______。A．10111110B．01110001C．11110010D．00101110

3.浮点数的一般表示形式为N=2E×F，其中E为阶码，F为尾数。以下关于浮点表示的叙述中，错误的是( )。两个浮点数进行相加运算，应首先( )。A．阶码的长度决定浮点表示的范围，尾数的长度决定浮点表示的精度B．工业标准IEEE754浮点数格式中阶码采用移码、尾数采用原码表示C．规格化指的是阶码采用移码、尾数采用补码D．规格化表示要求将尾数的绝对值限定在区间[O．5，1)

4.设某浮点数共12位，其中阶码含1位阶符共4位，以2为底，补码表示；尾数含1位数符共8位，补码表示，则规格化浮点数所能表示的最大正数是A.26-1B.27-1C.28-1D.29-1

更多“设32位浮点数格式如下。以下关于浮点数表示的叙述中，正确的是（请作答此空）。若阶码采用补码表示，为8位（含1位阶符），尾数采用原码表示，为24位（含1位数符），不考虑规格化，阶码的最大值为（ ）。 ”相关问题

  • 第1题：

    写出浮点加减运算步骤,并说明为什么要浮点数规格化。

    现有浮点数格式如下：1位阶符，6位阶码，1位数符，8位尾数，请写出浮点数所能表示的范围（只考虑正数值）。


    答案：-263～(1-2-8)×263

    解析：阶码使用移码表示，6位阶码1位阶符，故而能表示的最大值为263，而尾数用补码表示，故而8位尾数可表示的范围为-1～1-2-8。

  • 第2题：

    设浮点数字长16位，其中阶码5位(含1位阶符)，以2为底补码表示，尾数11位(含1位数符)补码表示，下列十进制数表示成规格化浮点数为多少?

    设浮点数字长16位,其中阶码5位(含1位阶符),以2为底补码表示,尾数11位(含1位数符)补码表示,下列十位进制数表示成规化浮点数为多少?

    3.5：(1)；79/512：(2)；-10-4：(3)；1010：(4)

    A．不能表示成浮点数

    B．11110 01001111000

    C．10010 01110000000

    D．11101 10111111110


    正确答案：C

  • 第3题：

    计算机中十六位浮点数的表示格式为

    某机器码为1110001010000000，

    若阶码为移码且尾数为反码，则其十进制真值为(7)；

    若阶码为移码且尾数为原码，则其十进制真值为(8)；

    若阶码为补码且尾数为反码，则其十进制真值为(9)；

    若阶码为补码且尾数为原码．则其十进制真值为(10)，将其规格化后的机器码为(11)。

    A．0.078125

    B．20

    C．20.969375

    D．1.25


    正确答案：B
    解析：(7)如果阶码为移码，由于阶码是4位二进制整数，设真值为X，根据整数移码定义：[X]移码=23+X(1110)2=(14)10，可求得阶码真值为6。如果尾数为反码，从符号位可判断尾数是正数，根据小数反码定义，正小数的反码就是其自身，可求得尾数的真值为：(0.01010000000)2=(2-1+2-4)=(0.3125)10，根据浮点数定义，该机器码真值为0.3125*26=20。(8)如果阶码为移码，同上，真值为6。如果尾数是原码，从符号位可判断尾数是正数，根据小数原码定义，正小数的原码就是其本身，可求得尾数的真值为0.3125。由此可知该机器码真值也是20。(9)如果阶码为补码，由于阶码是4位二进制整数，从符号位判断为负数，设真值为X，根据负整数定义[X]补码=24+X=(1110)2=(14)10，求得阶码的真值为-2。如果尾数为反码，同(7)一样求出尾数的真值为0.3125。这样，该机器码真值为0.3125*2-2=0.078125。(10)如果阶码是补码，尾数是原码，求出阶码和尾数的真值分别为-2和0.3125，这样该机器码的真值也是0.078125。(11)对浮点数进行规格化处理，规定浮点数的尾数部分用纯小数形式表示，当尾数的值不为0时，其绝对值应大于或等于0.5，用二进制表示为0.1XXX…XX(X为0或1)。对于不符合这一规定的浮点数，可改变阶码的大小并同时用左右移尾数的方法来满足这一规定。显然尾数0.01010000000不合要求，应左移1位，而阶码则应相应地减1，因此规格化处理后的阶码为1101，尾数为010100000000。

  • 第4题：

    下面是机器中浮点数的表示格式：

    设浮点数的基为2。若阶码用补码表示、尾数用原码表示，十进制数-51.875采用上述格式可表示为(7)；若阶码用移码表示、尾数用补码表示，该数可表示为(8)。

    A．0110 111001111100

    B．0110 011001111100

    C．0110 001110011111

    D．0101 011001111100


    正确答案：A
    解析：首先将-51.875转换为二进制表示：(-51.875)10=-110011.111=-0.110011111×2110，其中110是阶码，-0.110011111是尾数(绝对值大于0.5)。由于规格化表示格式中阶符和阶码共计4位，本题中阶码大于0，故采用补码时，这4位应该是[110]补=[110]原=0110。而采用原码表示尾数时，向[-0.110011111]原=1110011111后面添零补足12位，得111001111100。

  • 第5题：

    用12位寄存器表示规格化浮点数，左4位为阶码(含1位符号)，右8位为尾数(含1尾符)，阶码用移码，尾数用补码表示时，(-40)10表示成规定的浮点数是(2)。

    A．

    B．

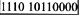
    C．

    D．


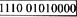    正确答案：B
    解析：浮点数中尾数最高位的真值为1的浮点数称为规格化浮点数。将浮点数规格化的方法是调整阶码使尾数满足下列关系：尾数为原码表示时，无论正负应满足1/2<|d|1，即小数点后的第一位数一定要为1。正数的尾数应为0.1x…x，负数的尾数应为1.1x…x。尾数用补码表示时，小数最高位应与数符符号位相反。正数应满足1/2d1，即0.1x…x；负数应满足-1/2＞d－1，即1.0x…x。(-40)10=-(0.101000)2×2+6，阶码6用移码表示为1110，尾数-0.101000用补码表示为1011000，尾数为8位所以加补一位0，因此选B。

  • 第6题：

    下面是某种计算机的32位短浮点数格式如图1.7

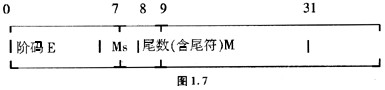
    其中，M为用定点小数表示的尾数的绝对值，占23位；Ms是尾数的符号位，占1位；Ms和M一起表示尾数。E为用定点整数表示的阶码，占8位。若机器表示中取阶码的基数为2，求采用下列五种不同编码方式时，浮点数-123625E-3(隐含基数为10)规格化后的机器码：

    阶码用补码方式、尾数用原码方式时，为(80)；

    阶码用补码方式、尾数用反码方式时，为(81)；

    阶码用移码方式、尾数用原码方式时，为(82)；

    阶码用移码方式、尾数用补码方式时，为(83)；

    阶码用移码方式、尾数用反码方式时，为(84)；

    A．10000111100001000110000000000000

    B．00000111100001000101111111111111

    C．10000111111110000101111111111111

    D．00000111111110111010000000000000


    正确答案：D

  • 第7题：

    设32位浮点数格式如下。以下关于浮点数表示的叙述中，正确的是（ ）。若阶码采用补码表示，为8位（含1位阶符），尾数采用原码表示，为24位（含1位数符），不考虑规格化，阶码的最大值为（请作答此空）。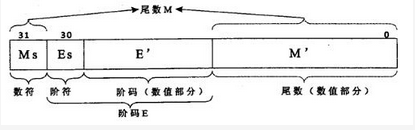

    A.255
    B.256
    C.127
    D.128

    答案：C
    解析：
    本题考察计算机数据的表示。浮点数所能表示的数值范围主要由阶码决定，所表示数值的精度则由尾数决定。八位阶码的最大值为127。

  • 第8题：

    某浮点机字长16位，其中，阶码5位(含1位阶符)，采用补码表示，基数为4；尾数儿位(含1位数符)，采用补码表示，且为规格化形式，则其可以表示的最小正数是()。


    答案：C
    解析：

  • 第9题：

    某浮点数格式如下：7 位阶码（包含一个符号位），9 位尾数（包含一个符号位）。若阶码用移码、尾数用规格化的补码表示，则浮点数所能表示数的范围是（）。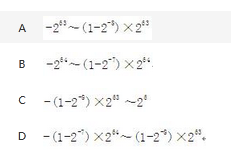


    答案：A
    解析：
    浮点数所能表示的数值范围如下：最大的正数

  • 第10题：

    （）在浮点数的表示中是隐含规定的

    • A、数符
    • B、阶符
    • C、尾数
    • D、阶码
    • E、阶码的底

    正确答案:E

  • 第11题：

    问答题
    设某浮点数格式为：字长12位，阶码6位，用移码表示，尾数6位，用原码表示，阶码在前，尾数（包括数符）在后，则按照该格式：已知X=-25/64，Y=2.875，求数据X、Y的规格化的浮点数形式。

    正确答案： [X]=-0.011001=-0.11001*2-1
    X.的符号：1
    X.的阶码：-1=-00001=（移码）011111
    X.的尾数：11001
    解析： 暂无解析

  • 第12题：

    单选题
    下列关于IEEE 754浮点数格式的叙述中，正确的是（　　）。
    A

    尾数和阶码均用原码表示

    B

    尾数用补码表示、阶码用原码表示

    C

    只能表示规格化数

    D

    可以表示规格化数和非规格化数


    正确答案： C
    解析：
    IEEE 754的浮点格式既可以表示规格化数，也可以表示非规格化数，同时，指数部分采用移码表示，尾数部分采用原码表示。

  • 第13题：

    设机器中浮点数的格式如下：

    其中阶码6位，包括1位符号位，尾数10位(含1位数符)，浮点数的基为2。阶码用补码表示，尾数用原码表示。对于十进制数-25.8375，当阶码用补码表示、尾数用原码表示时，得到的规格化机器码为(38)；当阶码用移码表示、尾数用原码表示时，得到的规格化机器码为(39)；当阶码用原码表示，尾数用补码表示时，得到的规格化机器码为(40)。

    A．1001011100111000

    B．1110101100111010

    C．1001011000111010

    D．1001011100111010


    正确答案：A

  • 第14题：

    用8位寄存器表示浮点数，左3位为阶码(含1位符号)，右5位为尾数(含1尾符)，阶码用移码，尾数用补码表示时，(-3.25)10的浮点数形式是(1)。

    A．

    B．

    C．

    D．


    正确答案：A
    解析：(-3.25)10=-0.1101×2+2，阶码2用移码表示为110，尾数-0.1101用补码表示为10011，所以选A。

  • 第15题：

    某计算机系统中，16位浮点数的表示格式如图6-1所示。其中阶码4位(含1位符号)为定点整数，尾数12位(含1位符号)为定点小数，设一个数机器码为1110001010000000。

    若阶码为移码且尾数为原码，则其十进制数真值为(2)；若阶码为补码且尾数为补码，则其十进制数真值规格化后的机器码为(3)。

    A．20

    B．25

    C．0.078125

    D．20.969375


    正确答案：A

  • 第16题：

    计算机中16位浮点数的表示格式如图1所示：

    某机器码为1110001010000000。

    若阶码为移码且尾数为反码，其十进制真值为(8)；

    若阶码为移码且尾数为原码，其十进制真值为(9)；

    若阶码为补码且尾数为反码，其十进制真值为(10)；

    若阶码为补码且尾数为原码，其十进制真值为(11)，将其规格化后的机器码为(12)。

    A．0.078125

    B．1.45

    C．20

    D．20.697395


    正确答案：C
    解析：本题考查计算机数据的编码，涉及原码、补码、反码和移码以及浮点数规格化处理。同一个数可以有不同的浮点表示形式，阶码的大小可以用来调节数值中小数点的位置。将数值数据表示成N=M+RE，M被称为N的尾数，E是N的指数或称阶码，而只是该阶码的基数。题中阶码用4位二进制整数1110表示，尾数用12位二进制小数001010000000表示，尾数中含有符号位，其最高位即符号位为0。下面具体解答各个问题。(8)如果阶码为移码，由于阶码是4位二进制整数，设真值为X，根据整数移码定义：[X]移码=23+X=(1110)2=(14)10，可此求得阶码真值为6。如果尾数为反码，从符号为可判断尾数是正数，根据小数反码定义，正小数的反码就是其自身，可求得尾数的真值为：(0.01010000000)2=(2-2+2-4)=(0.3125)10，根据浮点数定义，该机器码真值为0.3125+26=20。(9)如果阶码为移码，同上，真值为6。如果尾数是原码，从符号位可判断尾数是正数，根据小数原码定义，正小数的原码就是其本身，可求得尾数的真值位0.3125。这样该机器码的真值也是20。(10)如果阶码为补码，由于阶码是4位二进制整数，从符号位判断为负数，设真值为X，根据负整数定义[X]补码=24+x=(1110)2=(14)10，求得阶码的真值为-2。如果尾数为反码，同问题(8)一样求出尾数的真值为0.3125。这样，该机器码真值为0.3125*2-2=0.078125。(11)如果阶码是补码，尾数是原码，可分别参照问题(10)和问题(9)求出阶码和尾数的真值分别为-2和0.3125这样该机器码的真值也是0.078125。(12)这是对浮点数进行规格化处理。规定浮点数的尾数部分用纯小数形式表示，当尾数的值不为0时，其绝对值应大于或等于0.5，用二进制表示为0.1xxx…xx(x为0或1)。对于不符合这一规定的浮点数。可采用改变阶码的大小并同时左右移尾数的方法来满足这一规定。显然尾数0.01010000000不符合要求，应左移1位，而阶码则相应地减1，因此规格化处理后的阶码为1101，尾数为010100000000。

  • 第17题：

    计算机中十六位浮点数的表示格式为图1.4

    某机器码为1010001010000000。

    若阶码为移码且尾数为反码，则其真值为(60)；

    若阶码为移码且尾数为原码，则其真值为(61)；

    若阶码为补码且尾数为反码，则其真值为(62)；

    若阶码为补码且尾数为原码，则其真值为(63)，将其规格化后的机器码为(64)。

    A．0.00000001012

    B．2010

    C．1.2510

    D．20.96937510


    正确答案：C

  • 第18题：

    设32位浮点数格式如下。以下关于浮点数表示的叙述中，正确的是（ ）。若阶码采用补码表示，为8位（含1位阶符），尾数采用原码表示，为24位（含1位数符），不考虑规格化，阶码的最大值为（ ）。

    A.浮点数的精度取决于尾数M的位数，范围取决于阶码E的位数B.浮点数的精度取决于阶码E的位数，范围取决于尾数M的位数C.浮点数的精度和范围都取决于尾数M的位数，与阶码E的位数无关D.浮点数的精度和范围都取决于阶码E的位数，与尾数M的位数无关A.255 B.256 C.127 D.128


    正确答案：A,C

  • 第19题：

    设16位浮点数，其中阶符1位、阶码值6位、数符1位、尾数8位。若阶码用移码表示，尾数用补码表示，则该浮点数所能表示的数值范围是（ ）。



    答案：B
    解析：

  • 第20题：

    浮点数的一般表示形式为N=2E×F，其中E为阶码，F为尾数。以下关于浮点表示的叙述中，错误的是()。

    A.阶码的长度决定浮点表示的范围，尾数的长度决定浮点表示的精度
    B.工业标准IEEE754浮点数格式中阶码采用移码、尾数采用原码表示
    C.规格化指的是阶码采用移码、尾数采用补码
    D.规格化表示要求将尾数的绝对值限定在区间[0.5，1)

    答案：C
    解析：
    为了提高运算的精度，需要充分地利用尾数的有效数位，通常采取浮点数规格化形式，即规定尾数的最高数位必须是一个有效值，即1/2≤F＜1。在尾数用补码表示时，规格化浮点数应满足尾数最高数位与符号位不同，即当1/2≤F＜1时，应有0.1××…×形式；当-1≤M＜-1/2时，应有1.0××…×形式。需要注意的是，当M=-1/2时，对于原码来说是规格化数，而对于补码来说不是规格化数。

  • 第21题：

    设16位浮点数，其中阶符1位、阶码值6位、数符1位，尾数8位。若阶码用移码表示，尾数用补码表示，则该浮点数所能表示的数值范围是（3） 。


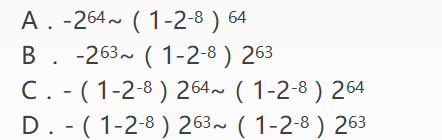    A.A
    B.B
    C.C
    D.D

    答案：B
    解析：

  • 第22题：

    浮点数的表示精度取决于（）的位数

    • A、数符
    • B、阶符
    • C、尾数
    • D、阶码
    • E、阶码的底

    正确答案:C

  • 第23题：

    单选题
    （）在浮点数的表示中是隐含规定的
    A

    数符

    B

    阶符

    C

    尾数

    D

    阶码

    E

    阶码的底


    正确答案： D
    解析： 暂无解析

相关内容