设A是n阶矩阵,且E+3A不可逆,则()。A.3是A的特征值B.-3是A的特征值C.1/3是A的特征值D.-1/3是A的特征值
题目
设A是n阶矩阵,且E+3A不可逆,则()。
A.3是A的特征值
B.-3是A的特征值
C.1/3是A的特征值
D.-1/3是A的特征值
相似考题
参考答案和解析
答案:D
解析:E+3A不可逆,即∣E+3A∣=0,即-3 * ∣(-1/3)E-A∣=0,所以A的特征值为-1/3。
更多“设A是n阶矩阵,且E+3A不可逆,则()。 ”相关问题
-
第1题:
设A、B都是n阶可逆矩阵,且(AB)2=I,则(BA)2的值为( )。
 答案:A解析:已知(AB)2=I,即ABAB=I,说明矩阵A可逆,且A-1=BAB,用A右乘上式两端即可得解
答案:A解析:已知(AB)2=I,即ABAB=I,说明矩阵A可逆,且A-1=BAB,用A右乘上式两端即可得解 -
第2题:
设n阶矩阵A可逆,且detA=a,求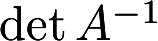 ,.
,.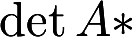 答案:解析:
答案:解析:
-
第3题:
设A是3阶矩阵,P = (α1,α2,α3)是3阶可逆矩阵,且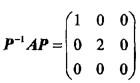 ,若矩阵Q=(α2,α1,α3),则Q-1AQ=( )。
,若矩阵Q=(α2,α1,α3),则Q-1AQ=( )。
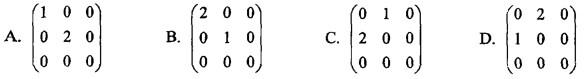 答案:B解析:提示:由条件知,λ1=1,λ2=2,λ3=0是矩阵A的特征值,而α1,α2,α3是对应的特征向量,故有
答案:B解析:提示:由条件知,λ1=1,λ2=2,λ3=0是矩阵A的特征值,而α1,α2,α3是对应的特征向量,故有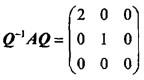 。
。 -
第4题:
设A1,A2分别为m阶,n阶可逆矩阵,分块矩阵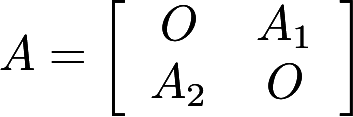 .证明:A可逆,且
.证明:A可逆,且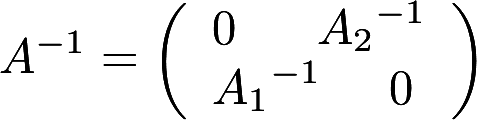 答案:解析:
答案:解析: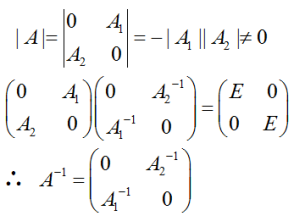
-
第5题:
设a为N阶可逆矩阵,则( ).《》( ) 答案:C解析:
答案:C解析:
