设A,B均为n阶矩阵,(I一B)可逆,则矩阵方程A＋BX=X的解X=()。

题目
设A,B均为n阶矩阵,(I一B)可逆,则矩阵方程A＋BX=X的解X=()。

相似考题

1.设A,B均为n阶可逆矩阵,求证:(AB)*=B*A*。

2.设A,B为n阶可逆矩阵,则().

3.设A、B都是n阶可逆矩阵，则

4.设A,B都是N阶矩阵,且存在可逆矩阵P,使得AP=B,则().A.A,B合同 B.A,B相似 C.方程组AX=0与BX=0同解 D.r(A)=r(B)

更多“设A,B均为n阶矩阵,(I一B)可逆,则矩阵方程A＋BX=X的解X=()。 ”相关问题

  • 第1题：

    设A,B都是n阶可逆矩阵,则().


    答案：B
    解析：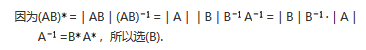

  • 第2题：

    设a为N阶可逆矩阵，则（ ）.《》（ ）


    答案：C
    解析：

  • 第3题：

    设A，B 均为n阶矩阵，A为可逆矩阵，证明：AB与BA相似。


    证明 用反证法：若E-BA不可逆则|E-BA|=0 使得(E-BA)X=O→X=BAX．令Y=AX则X=BY→Y≠O(否则X=O)又(E-AB)Y=Y-ABY=Y-AX=O这与E-AB可逆矛盾故E-BA可逆． 证明用反证法：若E-BA不可逆,则|E-BA|=0,,使得(E-BA)X=O→X=BAX．令Y=AX,则X=BY→Y≠O(否则X=O),又(E-AB)Y=Y-ABY=Y-AX=O,这与E-AB可逆矛盾,故E-BA可逆．

  • 第4题：

    设A、B都是n阶可逆矩阵，且(AB)2=I，则(BA)2的值为( )。



    答案：A
    解析：
    已知(AB)2=I，即ABAB=I，说明矩阵A可逆，且A-1=BAB，用A右乘上式两端即可得解

  • 第5题：

    设A与B均为n阶可逆矩阵，则只用初等行变换可把A变为B


    正确

相关内容