IEEE754浮点数x的二进制存储格式为(41360000)H,其对应的十进制值为( )A.11.5B.11.375C.11.355D.10.385

题目
IEEE754浮点数x的二进制存储格式为(41360000)H,其对应的十进制值为( )

A.11.5

B.11.375

C.11.355

D.10.385

相似考题

1.●在Pentium微处理器中，浮点数的格式采用IEEE754标准。假设一个规格化的32位浮点数如下：1 10000011 00101100000000000000000该数的十进制数值是 (29) 。(29) A．-2．75B．-16．75C．-20．75D．-18．75

2.在Pentium微处理器中，浮点数的格式采用IEEE754标准。假设一个规格化的32位浮点数如下 1 10000011 00101100000000000000000 该数的十进制数值是A．-2.75B．-16.75C．-20.75D．-18.75

3.下面关于计算机浮点数的叙述中，正确的是A．浮点数的绝对值不能大于1010B．十进制整数不能用浮点数精确表示C．Pentium微处理器中的浮点数采用40位二进制编码D．Pentium微处理器中浮点数的格式采用IEEE754标准

4.将十进制数0.84375表示成符合IEEE754标准的32位浮点数的是【 】。

参考答案和解析

答案：B

分析：将16进制展开后，可得二进制数格式为

0 100，0001，0 011，0110，0000，0000，0000，0000

S E M

指数e=100，0001，0－01111111=00000011=（3）10

包含隐藏位1的尾数1.M=1.011，0110，0000，0000，0000，0000

于是有 

x=（-1）^0*（1.M）*2^（E-127）

=+（1.011011）2*2^3

=（11.375）10

所以答案选B


更多“IEEE754浮点数x的二进制存储格式为(41360000)H,其对应的十进制值为( ) A.11.5B.11.375C.11.355D.10.385”相关问题

  • 第1题：

    十进制数89.75其对应的二进制可表示为()

    A.10001001.01110101

    B.1001001.10

    C.1011001.11

    D.10011000.11


    参考答案：C

  • 第2题：

    某计算机中一个16位的二进制代码1101 11100101 1000，它若表示的是一个浮点数，该浮点数格式如下：

    其中，阶码为移码(又叫增码)，基数为2，尾数用补码表示，则该浮点数的值(十进制)是【 】。


    正确答案：-6.625
    -6.625

  • 第3题：

    把短浮点数C1C90000H转换成为十进制数。

    将十六进制代码写成二进制形式，并分离出符号位、阶码和尾数。因为C1C90000H=11000001110010010000000000000000，所以符号位为1，阶码为10000011，尾数为10010010000000000000000。

    计算出阶码真值（移码减去偏置值），如下：

    10000011–1111111 = 100

    以规格化二进制数的形式写出此数，得到写成非规格化二进制数的形式，为11001.001。

    转换成十进制数，并加上符号位(11001.001)2=(25.125)10，所以，该浮点数为-25.125。

    为什么是负的，看到C1C90000H 不应该是正的么？


  • 浮点数的存储，尾数全都是以1为个位数的二进制小数
    也就是说尾数=10010001000000000000000
    其代表的是0.10010001000000000000000
    而真实值为1.1001000100000000000000

    这里的个位是被省略掉的，是默认为1的，所以我们看到的只是小数点后面的数字的记录，这种做法的好处就是能够覆盖更多的数字，一倍的差距。而计算机在从寄存器中读取该浮点数的记录并转化为我们可读的数字或者用于计算的时，已经把这个被省略的默认的“个位1”给重新加入进去了。所以才造成了视觉得偏差

    至于后面得出的结果，因为是C1C90000，说明首位符号位是1，次特性不会被阶码和位数的计算影响，确定是负数

    “规划和非规划化的区别是什么？”这个可能是某个教材中的作者惯用的叫法，我没什么印象了，有原文么？规格化则表示“0.6=1.00110011001（B）”等式中右半部的显示方式，区别在于小数点的位置和第一位是否为1“0.1010101”或“1001.101”这样都不是规格化显示

    C1C90000H=11000001110010010000000000000000 

    符号位=1

    阶码=10000011

    尾数=10010010000000000000000

    首先是符号位，判断正负
    然后是阶码，你刚才已经算出来是100，也就是十进制的4
    这里的尾数10010010000000000000000把后面的0都省略掉，就是1001001
    加上默认的个位1，可知该浮点数为
    1.1001001 * 2的4次方
    那么得出结果是小数点后移4位
    11001.001
    前半段换算可得25，后半段换算的0.125
    结果就是25.125
    然后再把符号加上，因为是负数
    所以结果是 -25.125

因为C1C90000H=11000001110010010000000000000000，所以符号位为1，阶码为10000011，尾数为10010010000000000000000。
人家都说了符号位是1 那就是负数嘛

十六进制和八进制是没有负数的所以转为十进制时要看符号位 也就是最高位是1还是0.。

1为负数 0为正数

（2）将十六进制代码写成二进制形式，并分离出符号位、阶码和尾数。因为C1C90000H=11000001110010010000000000000000，所以符号位为1，阶码为10000011，尾数为10010010000000000000000。
　　计算出阶码真值（移码减去偏置值），如下：
　　10000011–1111111 = 100
　　以规格化二进制数的形式写出此数，得到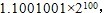写成非规格化二进制数的形式，为11001.001。
　　转换成十进制数，并加上符号位(11001.001)2=(25.125)10，所以，该浮点数为-25.125。

  • 第4题：

    IEEE754标准规定的64位浮点数格式中，符号位为1位，阶码为11位，尾数为52位，则它所能表示的最小规格化负数为()。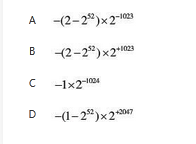


    答案：C
    解析：
    IEEE754标准规定64位浮点数格式中阶码11位，其中有1位符号位，则阶码中的数字位有10位。

  • 第5题：

    某数为IEEE754单精度浮点数格式表示为45100000H，则该数的值是（）

    • A、1.125×210
    • B、1.125×211
    • C、-1.125×211
    • D、-1.125×210

    正确答案:B

  • 第6题：

    C++常数0x45对应的十进制值为（）。


    正确答案:69

  • 第7题：

    若IEEE754单精度格式为（-1）s×（1.M）×2E-127，则十进制数-3/4表示成754标准的十六进制数据为（）。

    • A、3F200000H
    • B、BF200000H
    • C、3F400000H
    • D、BF400000H

    正确答案:D

  • 第8题：

    十进制数89.75其对应的二进制可表示为（）

    • A、10001001.01110101
    • B、1001001.10
    • C、1011001.11
    • D、10011000.11

    正确答案:C

  • 第9题：

    二进制数11000111对应的十进制数为199。


    正确答案:正确

  • 第10题：

    单选题
    某数为IEEE754单精度浮点数格式表示为45100000H，则该数的值是（）
    A

    1.125×210

    B

    1.125×211

    C

    -1.125×211

    D

    -1.125×210


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    ASCII码字符在计算机中存储时采用8位二进制其对应的最大十进制值是（）
    A

    127

    B

    128

    C

    255

    D

    256


    正确答案： B
    解析： 暂无解析

  • 第12题：

    问答题
    将下列十进制数转换为IEEE754单精度浮点数格式： （1）＋36.75 （2）－35/256

    正确答案： （1）+36.75=+100100.11B=1.0010011*25
    符号：0
    阶码：5+127=132=10000100
    尾数：00100110000000000000000
    单精度浮点数表示形式为01000010000100110000000000000000B＝42130000H
    （2）-35/256=-100011*2-8=-1.00011*2-3
    符号：1
    阶码：-3+127=124=01111100
    尾数：000110000000000000000000
    单精度浮点数表示形式为10111110000011000000000000000000B＝B.E0C0000H
    解析： 暂无解析

  • 第13题：

    IP地址长度为32位，以X．X．X．X格式表示，每个X为8位，其值为【 】，这种格式的地址常称为点分十进制地址。


    正确答案：0～255
    0～255 解析：IP地址长度为32位，以X．．X．X．X格式表示，每个X为8位，其值为 0～255，这种格式的地址常称为点分十进制地址。掌握计算机网络安全，TCP／IP协议。

  • 第14题：

    符合IEEE754标准的单精度浮点数0 10000101 1000100 10000000 00000000所表示的十进制数为【 】。


    正确答案：98.25
    98.25 解析：IEEE754标准中采用32位二进制表示浮点数，其表示方法(从左至右)分别是：1位符号+8位指数位+23位尾数。这里最高位是0，因此是正数，尾数是1000100　10000000　00000000，因此是(1.10001001)2，指数位为(10000101)2，指数位的处理方法是将指数位视为无符号整数，然后减去+127偏移量，得到的就是指数，这里(10000101)2=133，　133-127=6，所以26×(1.10001001)2=(1100010.01)2=(98.25)10

  • 第15题：

    十进制数5的单精度浮点数IEEE754代码为()。

    A.01000000101000000000000000000000
    B.11000000101000000000000000000000
    C.00100000101000000000000000000000
    D.01100000101000000000000000000000

    答案：A
    解析：
    IEEE754代码的第一位表示数符，5为正数，所以第一位为0，5=101B，=1.01乘以2的二次方，所以阶码为：偏置量+2=127+2=129，二进制表示为：10000001，由于阶码是用移码表示的，所以8位阶码部分为11000001，其余23位部分便是尾数部位，尾数部位则是0101，0000，0000，0000，0000，0000，0000。

  • 第16题：

    若IEEE754单精度格式为（-1）s×（1.M）×2E-127，则十进制数0.625表示成754标准的十六进制数据为（）。

    • A、3F200000H
    • B、BF200000H
    • C、3F400000H
    • D、BF400000H

    正确答案:A

  • 第17题：

    二进制值1001对应的十进制值为（）

    • A、4
    • B、9
    • C、6
    • D、7

    正确答案:B

  • 第18题：

    将下列十进制数转换为IEEE754单精度浮点数格式： （1）＋36.75 （2）－35/256


    正确答案:（1）+36.75=+100100.11B=1.0010011*25
    符号：0
    阶码：5+127=132=10000100
    尾数：00100110000000000000000
    单精度浮点数表示形式为01000010000100110000000000000000B＝42130000H
    （2）-35/256=-100011*2-8=-1.00011*2-3
    符号：1
    阶码：-3+127=124=01111100
    尾数：000110000000000000000000
    单精度浮点数表示形式为10111110000011000000000000000000B＝B.E0C0000H

  • 第19题：

    ASCII码字符在计算机中存储时采用8位二进制其对应的最大十进制值是（）。

    • A、127
    • B、128
    • C、255
    • D、256

    正确答案:C

  • 第20题：

    已知十进制数为10.125，其对应的二进制数为（）。

    • A、10000.110101
    • B、1010.000100100101
    • C、1010.001
    • D、10000.0010

    正确答案:C

  • 第21题：

    单选题
    二进制值1001对应的十进制值为（）
    A

    4

    B

    9

    C

    6

    D

    7


    正确答案： C
    解析： 暂无解析

  • 第22题：

    单选题
    已知十进制数为10.125，其对应的二进制数为（）。
    A

    10000.110101

    B

    1010.000100100101

    C

    1010.001

    D

    10000.0010


    正确答案： B
    解析： 暂无解析

  • 第23题：

    填空题
    C++常数0x145对应的十进制值为（）。

    正确答案： 325
    解析： 暂无解析

    • 相关内容