若一整系数多项式f(x)有有理根,则f(x)在有理数域上可约。( )
题目
相似考题
更多“若一整系数多项式f(x)有有理根,则f(x)在有理数域上可约。( )”相关问题
-
第1题:
(Ⅰ)证明拉格朗日中值定理:若函数f(x)在[a,b]上连续,在(a,b)内可导,则存在ξ∈(a,b),使得f(b)-f(a)=f'(ξ)(b-a);(Ⅱ)证明:若函数f(x)在x=0处连续,在(0,δ)(δ>0)内可导,且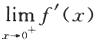 =A,则
=A,则 存在,且.
存在,且.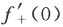 答案:解析:
答案:解析:

-
第2题:
若p(x)是F(x)中次数大于0的多项式,则类比素数的观点不可约多项式有多少条命题是等价的?()
- A、6.0
- B、5.0
- C、4.0
- D、3.0
正确答案:C -
第3题:
若f(x)模2之后得到的f(x)在Z2上不可约,可以推出什么?()
- A、f(x)在Q上不可约
- B、f(x)在Q上可约
- C、f(x)在Q上不可约或者可约
- D、无法确定
正确答案:A -
第4题:
f(x)在F[x]中可约的,且次数大于0,那么f(x)可以分解为几种不可约多项式的乘积?()
- A、无限多种
- B、2种
- C、唯一一种
- D、无法确定
正确答案:C -
第5题:
设K是个数域,K[x]中的多项式f(x),g(x),若有f=g,则可以得到什么?()
- A、f(x)=g(f(x))
- B、g(x)=f(f(x))
- C、f(x)=g(x)
- D、g(x)=f(g(x))
正确答案:C -
第6题:
域F上的一元多项式中的x是一个属于F的符号。
正确答案:错误 -
第7题:
判断题若f(x)与g(x)互素,则f(x)与g(x)的公因式都是零多项式。A对
B错
正确答案: 对解析: 暂无解析 -
第8题:
单选题f(x)(系数为an…a0)是一个次数n>0的本原多项式,q/p是有理根,那么可以得到f(x)=(px-q)g(x)成立,那么g(x)是什么多项式?()A任意多项式
B非本原多项式
C本原多项式
D无理数多项式
正确答案: D解析: 暂无解析 -
第9题:
单选题若f(x)模2之后得到的f(x)在Z2上不可约,可以推出什么?()Af(x)在Q上不可约
Bf(x)在Q上可约
Cf(x)在Q上不可约或者可约
D无法确定
正确答案: B解析: 暂无解析 -
第10题:
单选题不可约多项式f(x)的因式有哪些?()A只有零次多项式
B只有零次多项式和f(x)的相伴元
C只有f(x)的相伴元
D根据f(x)的具体情况而定
正确答案: A解析: 暂无解析 -
第11题:
单选题设K是个数域,K[x]中的多项式f(x),g(x),若有f=g,则可以得到什么?()Af(x)=g(f(x))
Bg(x)=f(f(x))
Cf(x)=g(x)
Dg(x)=f(g(x))
正确答案: C解析: 暂无解析 -
第12题:
判断题在数域K中多项式f(x)与g(x)若有f=g,则f(x)=g(x)。A对
B错
正确答案: 对解析: 暂无解析 -
第13题:
若f(x)在[a,b]上可积,则f(x)在[a,b]上连续。
正确答案:错误 -
第14题:
不可约多项式f(x)的因式有哪些?()
- A、只有零次多项式
- B、只有零次多项式和f(x)的相伴元
- C、只有f(x)的相伴元
- D、根据f(x)的具体情况而定
正确答案:B -
第15题:
若f(x)与g(x)互素,则f(x)与g(x)的公因式都是零多项式。
正确答案:错误 -
第16题:
f(x)(系数为an…a0)是一个次数n>0的本原多项式,q/p是有理根,那么可以得到f(x)=(px-q)g(x)成立,那么g(x)是什么多项式?()
- A、任意多项式
- B、非本原多项式
- C、本原多项式
- D、无理数多项式
正确答案:C -
第17题:
x^2+x+1在有理数域上是可约的。
正确答案:错误 -
第18题:
在数域K中多项式f(x)与g(x)若有f=g,则f(x)=g(x)。
正确答案:正确 -
第19题:
单选题一个次数大于0的整系数多项式f(x)在Q上可约,那么f(x)可以分解成两个次数比f(x)次数低的什么多项式的乘积。()A整系数多项式
B本原多项式
C复数多项式
D无理数多项式
正确答案: B解析: 暂无解析 -
第20题:
单选题若p(x)是F(x)中次数大于0的多项式,则类比素数的观点不可约多项式有多少条命题是等价的?()A6.0
B5.0
C4.0
D3.0
正确答案: B解析: 暂无解析 -
第21题:
单选题下列说法中正确的是( )。[2014年真题]A若f′(x0)=0,则f(x0)必须是f(x)的极值
B若f(x0)是f(x)的极值,则f(x)在点x0处可导,且f′(x0)=0
C若f(x0)在点x0处可导,则f′(x0)=0是f(x)在x0取得极值的必要条件
D若f(x0)在点x0处可导,则f′(x0)=0是f(x)在x0取得极值的充分条件
正确答案: B解析:
当f(x0)在点x0处可导时,若f(x)在x0处取得极值,则可知f′(x0)=0;若f′(x0)=0,f(x)在点x0未必取得极值,例如f(x)=x3在点x=0处有f′(0)=0,但x3在实数域内不存在极值点。 -
第22题:
判断题x^2+x+1在有理数域上是可约的。A对
B错
正确答案: 错解析: 暂无解析 -
第23题:
判断题若f(x)在[a,b]上可积,则f(x)在[a,b]上连续。A对
B错
正确答案: 对解析: 暂无解析
