有甲、乙、丙、丁、戊五个人,每个人头上戴一顶白帽子或者黑帽子,每个人显然只能看见别人头上帽子的颜色,看不见自己头上帽子的颜色。并且,一个人戴白帽子当且仅当他说真话,戴黑帽子当且仅当他说假话。已知: 甲说:我看见三顶白帽子一顶黑帽子。 乙说:我看见四顶黑帽子。 丙说:我看见一顶白帽子三顶黑帽子。 戊说:我看见四顶白帽子。 根据上述题干,下列陈述都是假的,除了( ) A.甲和丙都戴白帽子 B.乙和丙都戴黑帽子 C.戊戴白帽子,但丁戴黑帽子 D.丙戴黑帽子,但甲戴白帽子 E.丙和丁都戴白帽子
题目
有甲、乙、丙、丁、戊五个人,每个人头上戴一顶白帽子或者黑帽子,每个人显然只能看见别人头上帽子的颜色,看不见自己头上帽子的颜色。并且,一个人戴白帽子当且仅当他说真话,戴黑帽子当且仅当他说假话。已知:
甲说:我看见三顶白帽子一顶黑帽子。
乙说:我看见四顶黑帽子。
丙说:我看见一顶白帽子三顶黑帽子。
戊说:我看见四顶白帽子。
根据上述题干,下列陈述都是假的,除了( )
甲说:我看见三顶白帽子一顶黑帽子。
乙说:我看见四顶黑帽子。
丙说:我看见一顶白帽子三顶黑帽子。
戊说:我看见四顶白帽子。
根据上述题干,下列陈述都是假的,除了( )
A.甲和丙都戴白帽子
B.乙和丙都戴黑帽子
C.戊戴白帽子,但丁戴黑帽子
D.丙戴黑帽子,但甲戴白帽子
E.丙和丁都戴白帽子
B.乙和丙都戴黑帽子
C.戊戴白帽子,但丁戴黑帽子
D.丙戴黑帽子,但甲戴白帽子
E.丙和丁都戴白帽子
相似考题
参考答案和解析
答案:E
解析:
解这道题只能用假设法和归谬法。先假设甲的话为真,则甲戴白帽子,加起来共有四顶白帽子一顶黑帽子,于是乙和丙的话就是假的,于是乙和丙都戴黑帽子,这与A项的话为真的结果(一顶黑帽子)矛盾,因此A项的话不可能为真,必定为假。再假设乙的话为真,则他自己戴白帽子,共有一顶白帽子四顶黑帽子;这样,由于丙看不见他自己所戴帽子的颜色,当他说“我看见一顶白帽子三顶黑帽子”时,他所说的就是真话,于是他戴白帽子,这样乙和丙都戴白帽子,有两顶白帽子,与乙原来的话矛盾。所以,乙所说的只能是假话,他戴黑帽子。既然已经确定甲、乙都戴黑帽子,则戊所说的“我看见四顶白帽子”就是假话,戊也戴黑帽子。现假设丙的话为假,则他实际看见的都是黑帽子,他自己也戴黑帽子,于是五个人都戴黑帽子,这样,乙的话就是真话;但我们已经证明乙的话不可能为真,因此丙的话也不可能为假,于是丙和未说话的丁戴白帽子。最后结果是:甲、乙、戌说假话,戴黑帽子;丙、丁说真话,戴白帽子。所以,正确的选项是E项。##niutk
更多“有甲、乙、丙、丁、戊五个人,每个人头上戴一顶白帽子或者黑帽子,每个人显然只能看见别人头上帽子的颜色,看不见自己头上帽子的颜色。并且,一个人戴白帽子当且仅当他说真话,戴黑帽子当且仅当他说假话。已知: ”相关问题
-
第1题:
甲、乙、丙三个学生分别戴着三种不同颜色的帽子,穿着三种不同颜色的衣服去参加大运会志愿者服务活动。已知:(1)帽子和衣服的颜色都只有红、黄、白三种;(2)甲没戴红帽子,乙没戴黄帽子;(3)戴红帽子的学生没有穿白衣服;(4)戴黄帽子的学生穿着红衣服;(5)乙没有穿黄衣服。试问:对三人所戴帽子和所穿衣服判断正确的是( )。A.甲戴白色帽子,乙穿红色衣服
B.甲戴黄色帽子,穿白色衣服
C.乙穿白色衣服,丙戴红色帽子
D.甲穿红色衣服,丙穿白色衣服答案:C解析:根据(2)知道乙没有戴黄色的帽子。
首先设乙帽子为红色。由于(3)戴红帽子的学生没有穿白衣服,则乙没有穿白衣服。由于(5)乙没有穿黄衣服,则乙衣服为红色。但是与(4)戴黄帽子的学生穿着红衣服相矛盾,故乙帽子为红色是不可能的。
因此乙的帽子只能为白色。由于(2)甲没戴红帽子,则甲戴黄帽子,于是丙戴红帽子。根据(4)戴黄帽子的学生穿着红衣服,则甲穿红衣服。而(5)乙没有穿黄衣服,则乙穿白衣服,丙穿黄衣服。具体参见下表说明: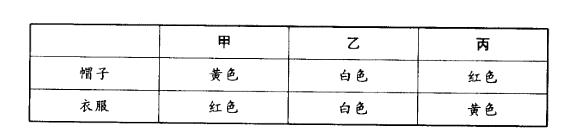
-
第2题:
甲、乙、丙三个学生分别戴着三种不同颜色的帽子,穿着三种不同颜色的衣服去参加一次争办奥运的活动。已知:(1)帽子和衣服的颜色都只有红、黄、蓝三种;(2)甲没戴红帽子,乙没戴黄帽子;(3)戴红帽子的学生没有穿蓝衣服;(4)戴黄帽子的学生穿着红衣服;(5)乙没有穿黄色衣服。试问:甲、乙、丙三人各什么颜色的帽子,穿什么颜色的衣服?A.甲戴蓝帽子穿红衣服。
B.乙戴蓝帽子穿蓝衣服。
C.丙戴黄帽子穿黄衣服。
D.甲戴蓝帽子穿蓝衣服。
E.丙戴红帽子穿红衣服。答案:B解析:第一步:明确维度和组度。3个维度:学生、帽子颜色和衣服颜色。3个组度:甲、乙、丙三人。第二步:画出对应表格,并将题干信息转移到表格中。
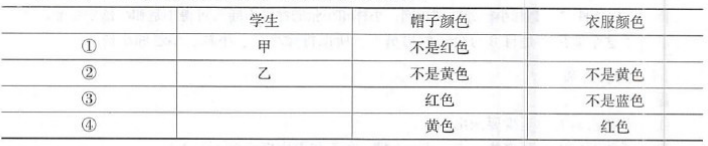
第三步:观察“重复出现”的内容作为突破口:(1)②④中帽子颜色都出现了“黄色”这一信息,可得乙不穿红衣服;又已知乙不穿黄衣服,所以乙只能穿蓝衣服。(2)由上一步可知②中“衣服颜色”一列为“蓝色”,此时②③中衣服颜色都出现了“蓝色”这一信息,可得:乙不戴红帽子,又已知乙不戴黄帽子,所以乙只能戴蓝帽子。(3)甲不戴红帽子,不戴乙的蓝帽子,只能戴黄帽子,再由④知穿红衣服。(4)剩下的丙则为戴红帽子穿黄衣服。 -
第3题:
保安员在雪地、沙漠行动,或者特大风戴口罩时不得把口罩带系在()。
- A、脖子上
- B、帽子上
- C、耳朵上
- D、头上
正确答案:B -
第4题:
穿戴防护用品的顺序是()
- A、穿防护服、戴口罩、戴防护镜、戴帽子、穿鞋套或胶鞋、戴手套
- B、戴口罩、戴帽子、穿防护服、戴防护镜、穿鞋套或胶鞋、戴手套
- C、戴帽子、穿防护服、戴口罩、戴防护镜、穿鞋套或胶鞋、戴手套
- D、穿防护服、戴帽子、戴口罩、戴防护镜、穿鞋套或胶鞋、戴手套
正确答案:C -
第5题:
衣服一般与()意思相同,但在古代还包括头上戴的帽子类。
- A、时装
- B、服装
- C、服饰
- D、衣裳
正确答案:D -
第6题:
穿鼠疫防护服的先后顺序为()
- A、穿内隔离衣裤→戴白帽子和小口罩→扎三角头巾→穿防蚤袜→穿高统雨靴→穿反背衣→戴大口罩→戴手套→戴护目风镜
- B、穿内隔离衣裤→戴白帽子和小口罩→扎三角头巾→穿反背衣→穿防蚤袜→穿高统雨靴→戴手套→戴大口罩→戴护目风镜
- C、穿内隔离衣裤→戴白帽子和小口罩→扎三角头巾→穿防蚤袜→穿高统雨靴→穿反背衣→戴手套→戴护目风镜→戴大口罩
- D、穿内隔离衣裤→戴白帽子和小口罩→扎三角头巾→穿反背衣→穿防蚤袜→穿高统雨靴→戴大口罩→戴手套→戴护目风镜
正确答案:A -
第7题:
根据六顶帽子思考法,控制整个思考过程的人是戴()的人。
- A、黑帽子
- B、黄帽子
- C、红帽子
- D、蓝帽子
正确答案:D -
第8题:
有小利、小美、小景、小真、小珑五个孩子在一起玩耍,有的孩子额头上沾了泥巴。显然,每个孩子只能看见别人头上有没有泥巴,而看不见自己头上有没有泥巴。头上沾有泥巴的孩子只说假话,只说假话的孩子头上一定沾有泥巴。同样,头上没泥巴的孩子只说真话,只说真话的孩子头上一定没有泥巴。已知:小利说:我看见三个人头上没泥巴,一个人头上有泥巴小美说:我看见四个人头上都有泥巴小景说:我看见四个人头上都没泥巴。小珑说:我看见一个人头上没泥巴,三个人头上有泥巴。由此,以下陈述一定为真的是()。
- A、小景头上没有泥巴
- B、小利和小真头上没有泥巴
- C、小美头上有泥巴
- D、小真和小珑头上有泥巴
正确答案:C -
第9题:
问答题有10个人站成一队,每个人头上都戴着一顶帽子,帽子有3顶红的,4顶黑的5顶白的。每个人不能看到自己的帽子,只能看到前面的人的,最后一个人能够看到前面9个人的帽子颜色,倒数第二个人能够看到前面8个人的帽子颜色,以此类推,第一个人什么也看不到。现在从最后面的那个人开始,问他是不是知道自己所带帽子的颜色,如果他回答不知道,就继续问前面的人。如果后面的9个人都不知道,那么最前面的人知道自己颜色的帽子吗?为什么?正确答案: 最后一个人不知道自己所戴帽子的颜色,那么他的帽子和剩下的两顶帽子属于两种以上的颜色,通过排除,知道他的帽子和剩下的两顶帽子分属于三种颜色,第九个人不能判断自己所戴帽子的颜色,也是如此,以此类推,第一个人就能知道自己帽子的颜色为白色。解析: 暂无解析 -
第10题:
单选题比赛中甲队要戴白帽子,乙队要戴蓝帽子,守门员要戴红帽子。这项比赛是()。A冰球比赛
B橄榄球比赛
C水球比赛
正确答案: B解析: 暂无解析 -
第11题:
单选题衣服一般与()意思相同,但在古代还包括头上戴的帽子类。A时装
B服装
C服饰
D衣裳
正确答案: C解析: 暂无解析 -
第12题:
问答题有4个人在做游戏,一人拿了5顶帽子,其中3顶是白的,2顶是黑的。让其余的3人——A、B、C三人站成三角形,闭上眼睛。他给每人戴上一顶白帽子,把两顶黑帽子藏起来,然后让同学们睁开眼睛,不许交流相互看,猜猜自己戴的帽子的颜色。A、B、C三人互相看了看最后异口同声正确地说出了他们所带帽子是白色的,他们是怎么推出来的?正确答案: 根据所给帽子的颜色,只能有3种可能,即黑黑白、黑白白、白白白,如果是黑黑白,那么戴白帽就能立即说出答案,而没有人说出,排除了这种可能;如果有黑帽的话,只有一只,那么戴白帽的人就能立即做出回答,而这时也没有人猜出,那么只有“白白白”这一种可能了。解析: 暂无解析 -
第13题:
一群人开舞会,每人头上都戴着一顶帽子。帽子只有黑白两种,黑的至少有一顶。每个人都能看到其他人帽子的颜色,却看不到自己的。主持人先让大家看看别人头上戴的是什么帽子,然后关灯,如果有人认为自己戴的是黑帽子,就拍自已的手。第一次关灯,没有声音。于是再开灯,大家再看一遍,关灯时仍然鸦雀无声。一直到第三次关灯,才有噼噼啪啪拍手的声音响起。问有多少人戴着黑帽子?A.一人。
B.两人。
C.三人。
D.四人。
E.无法判断。答案:C解析:第一步:明确情景设置。①至少一黑;②每个人都能看到其他人帽子的颜色,却看不到自己的。第二步:分析每一轮情况。

-
第14题:
有甲、乙、丙、丁、戊五个人,每个人头上戴一顶内帽子或者黑帽子,每个人显然只能看见别人头上帽子的颜色,看不见自己头上帽子的颜色。并且,一个人戴白帽子当且仅当他说真话,戴黑帽子当且仅当他说假话。已知:
甲说:我看见三顶白帽子一顶黑帽子。
乙说:我看见四顶黑帽子。
丙说:我看见一顶白帽子三顶黑帽子。
戊说:我看见四顶白帽子。
根据上述题干,下列陈述都是假的,除了( )
A、甲和丙都戴白帽子
B、乙和丙都戴黑帽子
C、戊戴白帽子,但丁戴黑帽子
D、丙戴黑帽子,但甲戴白帽子
E、丙和丁都戴白帽子答案:E解析:解这道题只能用假设法和归谬法。先假设甲的话为真,则甲戴白帽子,加起来共有四顶白帽子一顶黑帽子,于是乙和丙的话就是假的,于是乙和丙都戴黑帽子,这与A项的话为真的结果(一顶黑帽子)矛盾,因此A项的话不可能为真,必定为假。再假设乙的话为真,则他自己戴白帽子,共有一顶白帽子四顶黑帽子;这样,由于丙看不见他自己所戴帽子的颜色,当他说“我看见一顶白帽子三顶黑帽子”时,他所说的就是真话,于是他戴白帽子,这样乙和丙都戴白帽子,有两顶白帽子,与乙原来的话矛盾。所以,乙所说的只能是假话,他戴黑帽子。既然已经确定甲、乙都戴黑帽子,则戊所说的“我看见四顶白帽子”就是假话,戊也戴黑帽子。现假设丙的话为假,则他实际看见的都是黑帽子,他自己也戴黑帽子,于是五个人都戴黑帽子,这样,乙的话就是真话;但我们已经证明乙的话不可能为真,因此丙的话也不可能为假,于是丙和未说话的丁戴白帽子。最后结果是:甲、乙、戌说假话,戴黑帽子;丙、丁说真话,戴白帽子。所以,正确的选项是E项。 -
第15题:
销售人员在销售散装食品时必须持有效健康证明,操作时须戴()
- A、口罩、手套
- B、帽子
- C、口罩、手套、帽子
- D、手套、帽子
正确答案:C -
第16题:
“克什米尔就像是巴基斯坦头上的一顶帽子。如果我们允许印度取走走我们头上的这顶帽子,那就会永远受印度的白摆布,”这句话是谁说的()。
- A、尼赫鲁
- B、纳塞尔
- C、真纳
- D、格雷西
正确答案:C -
第17题:
订婚后女方必须()。
- A、头上带帽子
- B、头上带男方送来的帽子
- C、颈上带男方送来银饰
- D、颈上带男方送来的玉石
正确答案:B,C -
第18题:
男子在握手前应先脱下手套,摘下帽子。女子可以戴手套和帽子握手。
正确答案:正确 -
第19题:
比赛中甲队要戴白帽子,乙队要戴蓝帽子,守门员要戴红帽子。这项比赛是()。
- A、冰球比赛
- B、橄榄球比赛
- C、水球比赛
正确答案:C -
第20题:
多选题订婚后女方必须()。A头上带帽子
B头上带男方送来的帽子
C颈上带男方送来银饰
D颈上带男方送来的玉石
正确答案: D,A解析: 暂无解析 -
第21题:
单选题根据六顶帽子思考法,控制整个思考过程的人是戴()的人。A黑帽子
B黄帽子
C红帽子
D蓝帽子
正确答案: C解析: 暂无解析 -
第22题:
问答题一个牢房,里面关有3个犯人。因为玻璃很厚,所以3个犯人只能互相看见,不能听到对方所说的话。一天,国王命令下人给他们每个人头上都戴了一顶帽子,告诉他们帽子的颜色只有红色和黑色,但是不让他们知道自己所戴的帽子是什么颜色。在这种情况下,国王宣布两条命令如下:1.哪个犯人能看到其他两个犯人戴的都是红帽子,就可以释放谁;2.哪个犯人知道自己戴的是黑帽子,也可以释放谁。事实上,他们三个戴的都是黑帽子。只是他们因为被绑,看不见自己的罢了。很长时间,他们3个人只是互相盯着不说话。可是过了不久,聪明的A用推理的方法,认定自己戴的是黑帽子。您也想想,他是怎样推断的呢?正确答案: 在国王宣布过第1条命令后,过了一段时间,仍没人被释放。因此,可以证明3顶帽子中没有2顶红帽,也可以说三个人中可能有2黑1红,或者3黑。于是出现了两种情况:假设A戴的是红帽,于是他就看见了2顶黑的。B和C都可以看见1黑1红。但是既然红的在A头上,那么B和C都是黑的。那么B和C早就能确定自己带的是黑帽。所以A不可能戴红帽。因此A推定自己头上戴的肯定是黑帽。因为只有出现3顶黑帽,才没有人敢确定红帽是否在自己头上。解析: 暂无解析 -
第23题:
问答题有甲、乙、丙、丁、戊五个人,每个人头上戴一顶白帽子或者黑帽子,每个人显然只能看见别人头上帽子当且仅当他说真话,戴黑帽子当且仅当他说假话。已知:甲说:我看见三顶白帽子一顶黑帽子;乙说:我看见四顶黑帽子;丙说:我看见一顶白帽子三顶黑帽子;戊说:我看见四顶白帽子。根据上述条件,请推理谁说真话:?谁说假话?谁戴白帽子?谁戴黑帽子?正确答案: 用假设法和归谬法。
先假设甲的话为真,戴白帽子,加起来共有四顶白帽子一顶黑帽子,于是乙和丙的话就是假的,于是乙和丙都戴黑帽子,这与甲的话为真的结果(一顶黑帽子)矛盾,因此甲的话不可能为真,必定为假,甲戴黑帽子。
再假设乙的话为真,则他自己戴白帽子,共有一顶白帽子。四顶黑帽子;这样,由于丙看不见他自己所戴帽子的颜色,当他说:.“我看见一顶白帽子三顶黑帽子”时,他所说的就是真话,于是他戴白帽子,这样乙和丙都戴白帽子,有两顶白帽子,与乙原来的话矛盾,所以,乙所说的只能是假话,他戴黑帽子。
既然已经确定甲、乙都戴黑帽子,则戊所说的“我看见四顶白帽子”就是假话,戊也戴黑帽子。
丙说他看见一顶白帽子三顶黑帽子,如果未说话的丁戴白帽子。则他的话为真;若丁戴黑帽子,则他的话为假。现证明丙的话不可能为假,必定为真。假设丙的话为假,则未说话的丁也戴黑帽子,他自己也戴黑帽子,于是五个人都戴黑帽子,这样,乙说看见四顶黑帽子,就说的是真话;但我们已经证明乙的话不可能为真,因此丙的话也不可能为假,于是丙戴白帽子。
最后结果是:丙、乙说,真话,戴白帽子;甲、乙、戊说假话,戴黑帽子。解析: 暂无解析
