在教学生求平行四边形面积时,教师讲授如下:连接AC,因为三角形ABC与三角形CDA的三边分别相等,所以,这两个三角形全等,三角形ABC的面积等于1/2底乘高,所以,平行四边形ABCD的面积等于底乘高,命题得到证明。然后,教师列举了很多不同大小的平行四边形,要求学生求出它们的面积,结果每个问题都正确解决了。下课前,教师又布置了十几个类似的问题作为家庭作业。你认为这种教学有何弊端?( )A.抑制学生学习的主动性、独立性B.学生的思维和想象力被扼杀C.导致学生学习的主体地位缺失D.增强教师的教学能力
题目
在教学生求平行四边形面积时,教师讲授如下:连接AC,因为三角形ABC与三角形CDA的三边分别相等,所以,这两个三角形全等,三角形ABC的面积等于1/2底乘高,所以,平行四边形ABCD的面积等于底乘高,命题得到证明。然后,教师列举了很多不同大小的平行四边形,要求学生求出它们的面积,结果每个问题都正确解决了。下课前,教师又布置了十几个类似的问题作为家庭作业。
你认为这种教学有何弊端?( )
A.抑制学生学习的主动性、独立性
B.学生的思维和想象力被扼杀
C.导致学生学习的主体地位缺失
D.增强教师的教学能力
相似考题
更多“在教学生求平行四边形面积时,教师讲授如下:连接AC,因为三角形ABC与三角形CDA的三边分别相等,所以 ”相关问题
-
第1题:
在相似三角形的判定的复习课上,甲乙两位教师分别设计了如下的教学片段:
(甲教师)
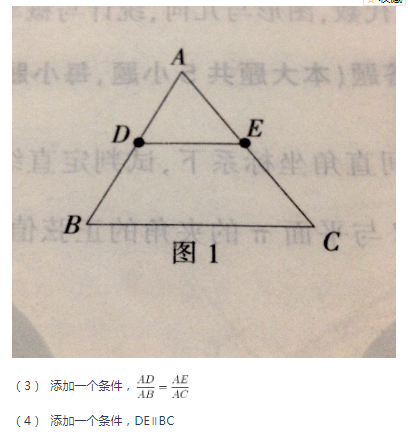
问题引入:如图1,在△ABC中,D、E分别是AB、AC上的两点,请你另外添加一个条件,使△ABC∽△ADE,并说明添加条件的理由。
预设学生回答。
(1) 添加一个条件,∠ADE=∠B
(2) 添加一个条件,∠AED=∠C
(5)依次说出判定方法和理由。
(乙教师)
教师提问:判定三角形相似有哪些方法?
预设学生回答:
(1)两角分别相等的两个三角形相似;
(2)两边成比例且夹角相等的两个三角形相似;
(3)三边成比例的两个三角形相似。
针对上述材料,完成下列任务。
(1)请分别对两位教师的教学设计片段进行评价,并简述理由。(10分)
(2)为了进一步巩固三角形相似的判定定理,请设计开放性的例题和习题各一个,并简述理由。(10分)
(3)简述数学教学中例题和习题设计的注意事项。(10分)答案:解析:本题主要考查数学教学设计内容。
1.分析两位教师的教学设计过程,针对不同内容给出对应的评价;2.根据教学要求及教学目标设计相应的例题与习题。 -
第2题:
如图2,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,依次类推,第2008个三角形的周长为( ) 答案:C解析:
答案:C解析: -
第3题:
教学设计一:在教学生求平行四边形面积时,教师讲授如下:连接AC,因为三角形ABC与三角形CDA的三边分别相等,所以,这两个三角形全等,三角形ABC的面积等于1/2底乘高,所以,平行四边形ABCD的面积等于底乘高,命题得到证明。然后,教师列举很多不同大小的平行四边形,要求学生求出它们的面积,结果每个问题都正确解决了。下课前,教师又布置了十几个类似的问题作为家庭作业。
教学设计二:教师引导学生分析问题,即如何把一个平行四边形变成一个长方形,然后组织学生自主探究,并获得计算平行四边形面积的公式。
问题:两则教学设计中教师的教学方法有何不同 两种教学方法对学生的学习将产生怎样的影响答案:解析:第一种是传授灌输式的教学方法,教师把学生置于知识的接受者的位置上.教师把知识传授作为自己的主要任务和目的,把主要精力放在检查学生对知识的掌握上,这样做,学生将整天处于被动应付,机械训练,死记硬背,简单重复的学习之中,学生学习的主动性、能动性、独立性被消蚀,思维和想象力被扼杀,学习的兴趣和热情被摧残,严重阻碍学生的发展,导致学生主体性缺失。 第二种是探究发现式的教学方法,教师把学生置于知识的发现者,探究者的位置上,教师将学习内容以问题形式间接呈现出来,引导学生主动、独立地探究学习。这样做,学生的主体性、能动性和独立性不断生成,使学习过程成为学生发现问题、提出问题、分析问题、解决问题的过程,培养了学生的批判意识和怀疑精神,鼓励学生对书本知识的质疑和对教师的超越,学生的创新精神和实践能力得到提升,促进了素质的提高。 -
第4题:
在相似三角形的判定的复习课上.甲乙两位教师分别设计了如下的教学片段:
(甲教师)
问题引入:如图1,在△ABC中,D、E分别是AB、AC上的两个点,请你另外添加一个条件,使△ABC—AADE.并说明添加条件的理由。
预设学生回答。
(1)添加一个条件
(2)添加一个条件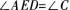
(3)添加一个条件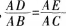
(4)添加一个条件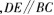
(5)…………依次说出判定方法和理由。
(乙教师)
教师提问:判定三角形相似有哪些方法
预设学生回答:
(1)两角分别相等的两个三角形相似;
(2)两边成比例且夹角相等的两个三角形相似;
(3)三边成比例的两个三角形相似。
针对上述材料,完成下列任务。
(1)请分别对两位教师的教学设计片段进行评价,并简述理由。(10分)
(2)为了进一步巩固三角形相似的判定定理,请设计开放性的例题和习题各一个,并简述理由。(10分)
(3)简述数学教学中例题和习题设计的注意事项。(10分)答案:解析:(1)两位教师的教学片段均属于课堂提问的类型。教师甲是应用提问。这种提问的目的是了解学生能否在理解新知识的基础上应用新知识和旧知识来解决问题。而教师乙采用的是复习、回忆提问。通过复习,回忆提问,使新旧知识相互连贯,强化了所学知识,还能检查学生的复习情况。
(2)例题:如图2在AABC中,点D,E分别在AB,AC边上,连结DE并延长交BC的延长线于点F,连结DC,BE,若∠BDE+∠BCE=1800
①写出图中三对相似三角形(注意:不得加字母和线)
②请在你所找出的相似三角形中选取一对,说明他们相似的理由。
习题:如图3,已知格点AABC,请在图4中分别画出与△ABC相似的格点△A1B1C1和格点△A2B2C2,并使△A1B1C1和△ABC的相似比等于2,而△ABC和△ABC的相似比等于根号5。(说明:顶点都在网格线交点处的三角形叫做格点三角形,友情提示:请在画出的三角形的顶点处标上相应的字母。)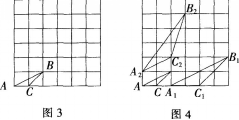
理由:两道例题设计具有梯度,难度逐渐增加,例l在老师的引导下充分巩固了三角形相似的性质,练习题设置具有开放性,能够充分发挥学生的创造力,调动学生主动思考的积极性。
(3)例题设计应具有目的性、典型性、启发性、科学性、变通性和有序性。具体来说,例题的选择要从学习目标和任务出发进行精选;要根据学生的学情进行例题的选配和安排,学习新知识必须建立在已有知识基础之上;更要具有提炼性。
习题是数学课堂教学的一个重要组成部分,他不仅有助于学生对知识的理解,巩固形成熟练的技能技巧,而且对学生智力发展和能力提高起着重要的作用,所以习题的设计应具有目的性、要及时、要有层次、要多样化、要有反馈。 -
第5题:
如下图,把三角形ABC 的三边分别延长1、2、3 倍,得到一个新的三角形,则新三角形的面积是原三角形ABC 面积的几倍?( ) A、15
A、15
B、16
C、17
D、18答案:D解析:

