递归算法在形式上是f(n)中调用f(n-1)
题目
递归算法在形式上是f(n)中调用f(n-1)
相似考题
更多“递归算法在形式上是f(n)中调用f(n-1)”相关问题
-
第1题:
已知递归函数f的定义如下:
int f(int n){
if(n<= 1)return 1;//递归结束情况f5=5*f3=5*3*f1
else return n*f(n-2); //递归
}
则函数调用语句f(5)的返回值是______。
正确答案:15
15 解析:函数递归调用,f(5)=5*f(3)=5*(3*f(1))=15。 -
第2题:
已知f(1)=1,f(2)=2,当n≥3时,f(n)= f(n-1)+f(n-2),编程求f(100)的值,应选择的算法为( )
A.解析法
B.穷举法
C.递归法
D.冒泡排序法
正确答案:C
-
第3题:
设求解某问题的递归算法如下: F(int n){ if n==1{ Move(1); } else{ F(n-1); Move(n); F(n-1); } } 求解该算法的计算时间时,仅考虑算法Move所进行的计算为主要计算,且Move为常数级算法,设算法Move的计算时间为k,当n=5时,算法F的计算时间为(42)。
A.7k
B.15k
C.31k
D.63k
正确答案:C
解析:直接递归算法的计算时间可以根据递归调用形式对应写出其递推关系式。按照题目中描述的算法形式可知,算法F的计算时间T(n)的递推关系式为T(n)=2T(n-1)+1,其中两次递归调用F(n-1)用时2T(n-1),算法Move的计算时间为常数,计为1。将上述递推关系式中常数1用k替换,求解可得T(n)=2n-1T(1)+k2i,易知T(1)=k,将n=5代入可得T(n)=2n-1T(1)+k2i=25-1k+k2i=24k+(20+21+22+23)k=31k。 -
第4题:
请编写一个函数long Fibo(int n), 该函数返回n的Fibonacci数。规则如下:n等于1或者2时,Fibonacci数为1,之后每个Fibonacci数均为止前两个数之和, 即:F(n)=F(n-1)+F(n-2)
注意:清使用递归算法实现该函数。
部分源程序已存在文件test1_2.cpp中。
请勿修改主函数main和其他函数中的任何内容,仅在函数Fibo的花括号中填写若干语句。如n=8时,结果是21。
文件test1_2.cpp清单如下:
include<iostream.h>
corlsh int N=8;
long Fibo(int n);
void main()
{
long f=Fibo(N);
couk<<f<<endl;
}
long Fibo(int n)
{
}
正确答案:long Fibo(int n) { if(n==1)return 1L; else if(n==2) return 1L; else return Fibo(n-1)+Fibo(n-2); }
long Fibo(int n) { if(n==1)return 1L; else if(n==2) return 1L; else return Fibo(n-1)+Fibo(n-2); } 解析:本题考查的是考生对于递归函数的熟练掌握。递归是指在调用函数的过程中出现调用该函数自身,这里递归的结束条件是n等于1或2,即已知数列前两项为1。其调用过程如下:如果函数的参数为l或者2就把返回值1返回调用函数;否则,就使用递推公式Fibo(n)=Fibo(n-1)+Fibo(n-2),把n-1和n-2作为参数调用原函数,即这是一个递归求值的过程(递推的过程)。 -
第5题:
能保证对所有的参数能够结束的递归函数是
A.int f(int n){if(n<1)return 1;else return n*f(n+1);}
B.int f(int n){if(n>1)return 1;else return n*f(n-1);}
C.int f(int n){if(abs(n)<1)return 1;else return n*f(n/2);}
D.int f(int n){if(n>1)return 1;else return n*f(n*2);)
正确答案:C
解析:递归函数的两个重要条件是要有结束和递归表达式。选项A、B、D无法结束。根据这两个条件可以进行判断出答案为C。 -
第6题:
已知递归函数f(n)的功能是计算1+2+…+n,且n≥1,应采用的代码段是______。
A.if n>1 then return 1 else return n+f(n-1)
B.if n>1 then return 1 else return n+f(n+1)
C.if n<1 then return 0 else return n+f(n-1)
D.if n<1 then return 0 else return n+f(n+1)
正确答案:C
解析:递归函数的目的是执行一系列调用,一直到达某一点,序列终止。为了保证递归函数正常执行,应该遵守下面的规则:
(1)每当一个递归函数被调用时,程序首先应该检查其基本的条件是否满足,例如,某个参数的值等于零,如果是这种情形,函数应停止递归。
(2)每当函数被递归调用时,传递给函数一个或多个参数,应该以某种方式变得“更简单”。即这些参数应该逐渐靠近上述基本条件。例如,一个正整数在每次递归调用时会逐渐变小,以至最终其值能到达零。
在本题中,f(n)的功能是解决1+2+…+n的累加问题,可用下面的递归公式表示f(n):
f(n)=0 (n=0)
f(n)=n+f(n-1) (n1)
因此可知,f(n)应采用的代码段为:
if n1
then return 0
else return n+f(n-1)。 -
第7题:
下面 ______ 是正确的递归函数,它保证对所有的参数能够结束。
A.int f(int n){ if(n<1) return 1; else return n*f(n+1); }
B.int f(int n){ if(n>1) return 1; else return n*f(n-1); }
C.int f(int n){ if(abs(n)<1) return 1; else return n*f(n/2); }
D.int f(int n){ if(n>1) return 1; else return n*f(n*2); }
正确答案:C
-
第8题:
递归函数f(n)的功能是计算1+2+…+n,且n≥1,则f(n)的代码段是(49)。
A.if n>1 then return 1 else return n+f(n-1)
B.if n>1 then return 1 else return n+f(n+1)
C.if n>1 then return 0 else return n+f(n+1)
D.if n<1 then return 0 else return n+f(n-1)
正确答案:D
解析:根据题意,当n1时结束递归,函数返回0,否则返回n+f(n-1)进行递归运算。 -
第9题:
菲波那契(Fibonacci)数列定义为
f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2)
据此可以导出,n>1时,有向量的递推关系式:
(f(n+1),f(n))=f(f(n),f(n-1))A
其中A是2*2矩阵(64)。从而,f(n+1),f(n)=(f(2),f(1))*(65).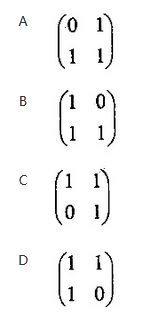 答案:D解析:本题考查数学应用的基础知识。
答案:D解析:本题考查数学应用的基础知识。
若矩阵A选取(64)中的D,则
(f(n),f(n-1))A=(f(n)+f(n-1),f(n))=(f(n+1),f(n))
由递推关系(f(n+1),f(n))=(f(n),f(n-1))A,
得到(f(n+1),f(n)):(f(n),f(n-1))A=f(n-1),f(n-2))A2=(f(n-2),f(n-3))A3=...
=(f(2),f(1)An-1=(1,1)An-1
这就给出了计算菲波那契数列的另一种算式。 -
第10题:
递归函数f(n)=f(n-1)+n(n>1)的递归出口是()
- A、 f(1)=0
- B、 f(1)=1
- C、 f(0)=1
- D、 f(n)=n
正确答案:B -
第11题:
对于以下递归函数f,intf(intn){returnf(n-1)+n;},调用f(4),其返回值为()
- A、10
- B、11
- C、0
- D、以上均不是
正确答案:D -
第12题:
单选题递归函数f(n)=f(n-1)+n(n>1)的递归出口是()Af(1)=0
Bf(1)=1
Cf(0)=1
Df(n)=n
正确答案: B解析: 暂无解析 -
第13题:
( 9 )下面的函数利用递归实现了求 1+2+3+ …… +n 的功能:
int sum ( int n ) {
if ( n==0 )
return 0;
else
return n+sum ( n-1 ) ;
}
在执行 sum ( 10 )的过程中,递归调用 sum 函数的次数是【 9 】 。
正确答案: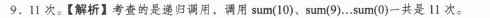
-
第14题:
将f=1+1/2+1/3+…+1/n转化成递归函数,其递归体是()。A、f(1)=0
B、f(1)=1
C、f(0)=1
D、f(n)=f(n-1)+1/n
参考答案:D
-
第15题:
下列各项中(r表示利率、n表示时期),可用于根据年金(用R表示)计算终值(用F表示)的是( )。
A.F=R×r(1+r)n/[(1+r)n-1]
B.F=R×[(1+r)n-1]/r
C.F=R×r/×[(1+r)n-1]
D.F=R×[(1+r)n-1]/r(1+r)n
正确答案:B
已知年金求终值。 -
第16题:
设有一个递归算法如下 im fact(int n){ if(n<=0)return 1; else return n * fact(n-1); } 下面正确的叙述是(35)。
A.计算fact(n)需要执行n次函数调用
B.计算fact(n)需要执行n+1次函数调用
C.计算fact(n)需要执行n+2次函数调用
D.计算fact(n)需要执行n-1次函数调用
正确答案:B
解析:连同其他函数调用fact和递归调用次数,计算fact(n)需要执行n+1次函数调用。 -
第17题:
设求解某问题的递归算法如下:
F(int n){
if n=1 {
Move(1)
}else{
F(n-1);
Move(n);
F(n-1);
}
}
求解该算法的计算时间时,仅考虑算法Move所做的计算为主要计算,且Move为常数级算法。则算法F的计算时间T(n)的递推关系式为(9);设算法Move的计算时间为k,当 n=4时,算法F的计算时间为(10)。
A.T(n)=T(n-1)+1
B.T(n)=2T(n-1)
C.T(n)=2T(n-1)+1
D.T(n)=2T(n+1)+1
正确答案:C
-
第18题:
已知递归函数f(n)的功能是打印n,n-1,…,1,且n>=1,应采用的代码段是(42)。
A.if n>1 then f(n-1); printf("% d",n);
B.if n<1 then f(n+1); printf("% d", n);
C.printf("% d",n); if n>1 then f(n-1);
D.printf("% d", n); if n<1 then f(n+1);
正确答案:C
解析:n等于1时,递归结束,当n>1时递归打印n-1。 -
第19题:
菲波那契(Fibonacci)数列定义为 f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2) 据此可以导出,n>1时,有向量的递推关系式: (f(n+1),f(n))=f(f(n),f(n-1))A 其中A是2*2矩阵( )。从而,(f(n+1),f(n)=(f(2),f(1))*( )
A.
 B.
B. C.
C. D.
D. A.An-1B.AnC.An+1D.An+2正确答案:D,A
A.An-1B.AnC.An+1D.An+2正确答案:D,A
-
第20题:
菲波那契(Fibonacci)数列定义为
f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2)
据此可以导出,n>1时,有向量的递推关系式:
(f(n+1),f(n))=f(f(n),f(n-1))A
其中A是2*2矩阵()。从而,f(n+1),f(n)=(f(2),f(1))*(65).A.An-1
B.An
C. An+1
D. An+2答案:A解析:本题考查数学应用的基础知识。
若矩阵A选取(64)中的D,则
(f(n),f(n-1))A=(f(n)+f(n-1),f(n))=(f(n+1),f(n))
由递推关系(f(n+1),f(n))=(f(n),f(n-1))A,
得到(f(n+1),f(n)):(f(n),f(n-1))A=f(n-1),f(n-2))A2=(f(n-2),f(n-3))A3=...
=(f(2),f(1)An-1=(1,1)An-1
这就给出了计算菲波那契数列的另一种算式。 -
第21题:
设n的初值为正整数,设计一个递归算法如下:int fact(int n){if(n<=0)return 1;else return(n*fact(n-1));}以下叙述中,正确的是______。A.计算fact(n)需要执行n+2次函数调用
B.计算fact(n)需要执行n+1次函数调用
C.计算fact(n)需要执行n次函数调用
D.计算fact(n)需要执行n-1次函数调用答案:B解析:本题考查函数递归调用方面的相关知识。递归法是描述算法的一种强有力的方法,其思想是:将N=n时不能得出解的问题,设法递归(压栈)转化为求n-1,n-2,…的问题,一直到N=0或1的初始情况,由于初始情况的解可以给出,因此,开始层层退栈得到N=2,3,…,n时的解,得到最终结果。本题中,主程序调用fact(n)称为外部调用,其他调用称为内部调用,直到调用fact(0)为止。fact(n)调用fact(n-1),fact(n-1)调用fact(n-2)……fact(1)调用fact(0),内部调用n次,外部调用一次,共n+1次。 -
第22题:
设有一个递归算法如下: int fact(int n) { //n大于等于0 if(n<=0) return 1; else return n*fact(n-1); } 则计算fact(n)需要调用该函数的次数为()
- A、 n+1
- B、 n-1
- C、 n
- D、 n+2
正确答案:A -
第23题:
判断题将f=1+1/2+1/3+…+1/n转化为递归函数时,递归部分为f(n)=f(n-1)+1/n,递归结束条件为f(1)=1。()A对
B错
正确答案: 对解析: -
第24题:
单选题设有一个递归算法如下: int fact(int n) { //n大于等于0 if(n<=0) return 1; else return n*fact(n-1); } 则计算fact(n)需要调用该函数的次数为()An+1
Bn-1
Cn
Dn+2
正确答案: A解析: 特殊值法。设n=0,易知仅调用一次fact(n)函数,故选A。
