( 8 )已知递归函数 f 的定义如下:int f(int n){if (n <= 1) return 1; // 递归结束情况else return n * f(n-2); // 递归 }则函数调用语句 f(5) 的返回值是 【 8 】 。
题目
( 8 )已知递归函数 f 的定义如下:
int f(int n)
{
if (n <= 1) return 1; // 递归结束情况
else return n * f(n-2); // 递归 }
则函数调用语句 f(5) 的返回值是 【 8 】 。
相似考题
更多“( 8 )已知递归函数 f 的定义如下:int f(int n){if (n = 1) return 1; // 递归结束情况else return n * f(n-2); // 递归 }则函数调用语句 f(5) 的返回值是 【 8 】 。”相关问题
-
第1题:
已知递归函数fun的定义如下: int fun(int n) { if(n<=1)return 1;//递归结束情况 else return n*fun(n-2);//递归 } 则函数调用语句fun(5)的返回值是( )。
A.5
B.12
C.15
D.30
正确答案:C
解析:递归函数fun被定义为含有参数int n返回整型.其中 fun函数递归调用本身,当n=1时,fun返回1,如果大于1那么执行n*fun(n-2)。所以,当n等于5时,执行5*fun(3);当n等于3时继续调用fun,3*fun(1),即fun(5)=5*(3*fun(1)),答案为15。 -
第2题:
有如下递归函数:
int Fun(int n){
if(n<=1) return 1;
______
}
请补充完整,使得函数Fun能够正确计算形参n的阶乘。
正确答案:else return n*Fun(n-1);
else return n*Fun(n-1); 解析:此题考查的是递归函数。函数Fun中的参数n小于2时,Fun函数返回1,其余返回值为n*Fun(n-1)。 -
第3题:
阅读以下函数说明和C语言函数,将应填入(n)处的字句写在答题纸的对应栏内。
【函数2.1说明】
递归函数sum(int a[], int n)的返回值是数组a[]的前n个元素之和。
【函数2.1】
int sum (int a[],int n)
{
if(n>0) return (1);
else (2);
}
【函数2.2说明】
有3个整数,设计函数compare(int a,int b,int c)求其中最大的数。
【函数2.2】
int compare (int a, int b, int c )
{ int temp, max;
(3) a:b;
(4) temp:c;
}
【函数2.3说明】
递归函数dec(int a[],int n)判断数组a[]的前n个元素是否是不递增的。不递增返回 1,否则返回0。
【函数2.3】
int dec( int a[], int n )
{
if(n<=1) return 1;
if(a[0]<a[1]) return 0;
return (5);
}
正确答案:(1)a[n-1]+sum(an-1)或者a[0]+sum(a+1n-1); (2)return 0; (3)temp=(a>b)? (4)max=(temp>c)? (5)dec(a+1n-1);
(1)a[n-1]+sum(a,n-1)或者a[0]+sum(a+1,n-1); (2)return 0; (3)temp=(a>b)? (4)max=(temp>c)? (5)dec(a+1,n-1); 解析:本题考查C语言函数和一些基本运算。
下面我们分别来分析这几个函数。在函数2.1中,题目要求用此递归函数求数组前 n个元素之和。递归函数的特点是在函数体中不停地调用函数本身,只是将其函数的参数范围改变。题目中要求我们求数组前n个元素之和,我们可以这样理解,即前n个元素之和等于第n个元素加上前n-1个元素之和,现在的问题转化成如何求前n-1个元素之和。同样的道理,可以将求前n-1个元素之和转化成求前n-2个元素之和,直到这个数小于0。从函数2.1的代码中可以知道,在计算以前,首先判断n与0的关系,如果n小于0,说明数组中无元素,因此,返回0值;如果n大于等于0,说明数组中有元素,应该返回的结果是第n个元素加上前n-1个元素之和,而前n-1个元素之和是调用函数本身来计算的。因此,第(1)空和第(2)空的答案分别是a[n-1)+sum(a,n-1),return()。
在函数2.2中,题目要求我们在三个数中取最大数,在数学中,我们从三个数中取最大数时,一般是首先拿其中两个数比较,取较大的数再与第三个数比较,再取其较大的数,这个数就是三个数中的最大数。从函数2.2的代码中知道,三个数a、b、c,两个整型变量temp与max。根据求三个数中最大数的数学过程和函数中已给出的代码可知,第(3)空处语句应该为temp=(a>b)?a:b,求得a、b中较大数并存放在变量temp中。第(4)空处语句为max=(temp>c)?temp:c。
在函数2.3中,题目要求判断数组a[]的前n个元素是否是不递增的。不递增返回1,否则返回0。要判断前n个元素是否是不递增的,需要判断前n-1个元素是否是不递增的,以及第n个元素与第n-1个元素的关系。此处与函数2.1一样,用的都是递归函数,只是出口不同,在函数2.1中,只要数组中没有元素了,递归结束,这里只要第n个元素大于第n-1个元素,则返回0,递归结束。又由if(a[0]a[1])语句可知,在每次调用函数时,都将其数组中的第一个元素与第二个元素比较来作为递归的出口,如果结果为假,就说明数组的前面两项的关系是不递增的,在下次调用中不用再考虑第一项。因此第(5)空应该是dec(a+1,n-1)。 -
第4题:
请编写一个函数long Fibo(int n), 该函数返回n的Fibonacci数。规则如下:n等于1或者2时,Fibonacci数为1,之后每个Fibonacci数均为止前两个数之和, 即:F(n)=F(n-1)+F(n-2)
注意:清使用递归算法实现该函数。
部分源程序已存在文件test1_2.cpp中。
请勿修改主函数main和其他函数中的任何内容,仅在函数Fibo的花括号中填写若干语句。如n=8时,结果是21。
文件test1_2.cpp清单如下:
include<iostream.h>
corlsh int N=8;
long Fibo(int n);
void main()
{
long f=Fibo(N);
couk<<f<<endl;
}
long Fibo(int n)
{
}
正确答案:long Fibo(int n) { if(n==1)return 1L; else if(n==2) return 1L; else return Fibo(n-1)+Fibo(n-2); }
long Fibo(int n) { if(n==1)return 1L; else if(n==2) return 1L; else return Fibo(n-1)+Fibo(n-2); } 解析:本题考查的是考生对于递归函数的熟练掌握。递归是指在调用函数的过程中出现调用该函数自身,这里递归的结束条件是n等于1或2,即已知数列前两项为1。其调用过程如下:如果函数的参数为l或者2就把返回值1返回调用函数;否则,就使用递推公式Fibo(n)=Fibo(n-1)+Fibo(n-2),把n-1和n-2作为参数调用原函数,即这是一个递归求值的过程(递推的过程)。 -
第5题:
设有如下函数定义
int fun(int k)
{if(k<1) return 0:
else if(k==1) return 1:
else return fun(k一1)+1:
}
若执行调用语句:n=fun(3);,则函数fun总共被调用的次数是
A.2
B.3
C.4
D.5
正确答案:B
解析:函数fun总共被调用了3次,即fun(3)、fun(2)和fun(13) -
第6题:
能保证对所有的参数能够结束的递归函数是
A.int f(int n){if(n<1)return 1;else return n*f(n+1);}
B.int f(int n){if(n>1)return 1;else return n*f(n-1);}
C.int f(int n){if(abs(n)<1)return 1;else return n*f(n/2);}
D.int f(int n){if(n>1)return 1;else return n*f(n*2);)
正确答案:C
解析:递归函数的两个重要条件是要有结束和递归表达式。选项A、B、D无法结束。根据这两个条件可以进行判断出答案为C。 -
第7题:
设有一个递归算法如下: int fact(int n){ if(n<=0)return 1; else return n*fact(n-1); } 下面正确的叙述是(35)。
A.计算fact(n)需要执行n次函数调用
B.计算fact(n)需要执行n+1次函数调用
C.计算fact(n)需要执行n+2次函数调用
D.计算fact(n)需要执行n-1次函数调用
正确答案:B
解析:主程序调用fact(n)称为外部调用,其他调用为内部调用,直到调用fact(0)为止,fact(n)调用fact(n-1),fact(n-1)调用fact(n-2),…,fact(1)调用fact(0),内部调用n次,外部调用1次,总共n+1次。 -
第8题:
下面 ______ 是正确的递归函数,它保证对所有的参数能够结束。
A.int f(int n){ if(n<1) return 1; else return n*f(n+1); }
B.int f(int n){ if(n>1) return 1; else return n*f(n-1); }
C.int f(int n){ if(abs(n)<1) return 1; else return n*f(n/2); }
D.int f(int n){ if(n>1) return 1; else return n*f(n*2); }
正确答案:C
-
第9题:
递归函数f(n)的功能是计算1+2+…+n,且n≥1,则f(n)的代码段是(49)。
A.if n>1 then return 1 else return n+f(n-1)
B.if n>1 then return 1 else return n+f(n+1)
C.if n>1 then return 0 else return n+f(n+1)
D.if n<1 then return 0 else return n+f(n-1)
正确答案:D
解析:根据题意,当n1时结束递归,函数返回0,否则返回n+f(n-1)进行递归运算。 -
第10题:
设n的初值为正整数,设计一个递归算法如下:int fact(int n){if(n<=0)return 1;else return(n*fact(n-1));}以下叙述中,正确的是______。A.计算fact(n)需要执行n+2次函数调用
B.计算fact(n)需要执行n+1次函数调用
C.计算fact(n)需要执行n次函数调用
D.计算fact(n)需要执行n-1次函数调用答案:B解析:本题考查函数递归调用方面的相关知识。递归法是描述算法的一种强有力的方法,其思想是:将N=n时不能得出解的问题,设法递归(压栈)转化为求n-1,n-2,…的问题,一直到N=0或1的初始情况,由于初始情况的解可以给出,因此,开始层层退栈得到N=2,3,…,n时的解,得到最终结果。本题中,主程序调用fact(n)称为外部调用,其他调用称为内部调用,直到调用fact(0)为止。fact(n)调用fact(n-1),fact(n-1)调用fact(n-2)……fact(1)调用fact(0),内部调用n次,外部调用一次,共n+1次。 -
第11题:
设有一个递归算法如下: int fact(int n) { //n大于等于0 if(n<=0) return 1; else return n*fact(n-1); } 则计算fact(n)需要调用该函数的次数为()
- A、 n+1
- B、 n-1
- C、 n
- D、 n+2
正确答案:A -
第12题:
判断题将f=1+1/2+1/3+…+1/n转化为递归函数时,递归部分为f(n)=f(n-1)+1/n,递归结束条件为f(1)=1。()A对
B错
正确答案: 对解析: -
第13题:
( 21 )计算斐波那契数列第 n 项的函数定义如下:
Int fib(int n){
if (n == 0) return 1;
else if (n == 1) return 2;
else return fib(n-1)+fib(n-2);
}
若执行函数调用表达式 fib(2) ,函数 fib 被调用的次数是
A ) 1
B ) 2
C ) 3
D ) 4
正确答案:C
-
第14题:
设有一个递归算法如下int fact(intn){//n 大于等于0 if(n<=0)return 1; else return n* fact(n--); }则计算fact(n)需要调用该函数的次数为(30)次。
A.n
B.n+1
C.n+2
D.n-1
正确答案:B
解析:n--为先使用后自减所以调用n-1次时的值为0终止调用 -
第15题:
下述程序的输出结果是()。includeint f(n)int n;{if(n==0 | | n==1)return 3;return n 下述程序的输出结果是( )。 #include <stdio.h> int f(n) int n; { if(n==0 | | n==1) return 3; return n-f(n-2); } void main() {printf("\n%d",f(10)); }
A.3
B.8
C.9
D.10
正确答案:A
解析:本题定义了一个递归函数f()。当传入的参数n等于1或0时返回3,否则返回n-f(n-2)。所以f(10)=10-f(8)=10- (8—f(6))=10-8+(6-f(4))=10-8+6-(4-f(2))=10-8+6-4+(2-f(0))=10-8+6-4+2-3=3。故本题应该选择A。 -
第16题:
设有一个递归算法如下 im fact(int n){ if(n<=0)return 1; else return n * fact(n-1); } 下面正确的叙述是(35)。
A.计算fact(n)需要执行n次函数调用
B.计算fact(n)需要执行n+1次函数调用
C.计算fact(n)需要执行n+2次函数调用
D.计算fact(n)需要执行n-1次函数调用
正确答案:B
解析:连同其他函数调用fact和递归调用次数,计算fact(n)需要执行n+1次函数调用。 -
第17题:
已知有函数f的定义如下:
int f( ){
static int s=0;
s+=2:
return s;
}
则在某程序中第二次执行函数调用语句f( );时,函数f的返回值是______。
正确答案:4
4 -
第18题:
已知递归函数f(n)的功能是计算1+2+…+n,且n≥1,应采用的代码段是______。
A.if n>1 then return 1 else return n+f(n-1)
B.if n>1 then return 1 else return n+f(n+1)
C.if n<1 then return 0 else return n+f(n-1)
D.if n<1 then return 0 else return n+f(n+1)
正确答案:C
解析:递归函数的目的是执行一系列调用,一直到达某一点,序列终止。为了保证递归函数正常执行,应该遵守下面的规则:
(1)每当一个递归函数被调用时,程序首先应该检查其基本的条件是否满足,例如,某个参数的值等于零,如果是这种情形,函数应停止递归。
(2)每当函数被递归调用时,传递给函数一个或多个参数,应该以某种方式变得“更简单”。即这些参数应该逐渐靠近上述基本条件。例如,一个正整数在每次递归调用时会逐渐变小,以至最终其值能到达零。
在本题中,f(n)的功能是解决1+2+…+n的累加问题,可用下面的递归公式表示f(n):
f(n)=0 (n=0)
f(n)=n+f(n-1) (n1)
因此可知,f(n)应采用的代码段为:
if n1
then return 0
else return n+f(n-1)。 -
第19题:
已知递归函数fun的定义如下: int fun(int n) { if(n<=1)return1;//递归结束情况 else return n*fun(n-2);//递归 } 则函数调用语句fun(5)的返回值是( )。
A.5
B.12
C.15
D.30
正确答案:C
解析:递归函数fun被定义为含有参数int n,返同整型。其中fun函数递归调用本身,当n=1时,fun返回1,如果大于1那么执行n*fun(n-2)。所以,当n等于5时,执行5*fun(3);当3时继续调用fun,3*fun(1),即fun(5)=5*(3*fun(1)),答案为15。 -
第20题:
下列函数中,哪项是正确的递归函数( )。
A int Fun(int n)
{
if(n<1) return 1;
else return n*Fun(n+1);
}
B) int Fun(ira n)
{
if(abs(n)<1) return 1;
else return n*Fun(n/2);
}
C) int Fun(int n)
{
if(n>1) return 1;
else return n*Fun(n*2)1
}
D) int Fun(int n)
{
if(n>1) return 1;
else retun n*Fun(n-1);
}
A.A
B.B
C.C
D.D
正确答案:B
解析:本题考查递归函数这个知识点。递归函数由递归出口和递归体两部分组成:递归出口给出了递归终止的条件;递归体给出了递归的方式。对于选项A,当参数n>=1时,不满足递归调用的结束条件;对于选项C,当参数n=0时,不满足递归调用的结束条件;对于选项D,当参数n:2时,不满足递归调用的结束条件。 -
第21题:
已知递归函数f的定义如下:
int f(int n)
{
if(n <=1)return 1; //递归结束情况
else return n*f(n-2); //递归}
则函数调用语句f(5)的返回值是【 】。
正确答案:15
15 解析:本题考查的是递归算法的分析。一个直接或间接地调用自身的算法称为递归算法。在一个递归算法中,至少要包含一个初始值和一个递归关系。本题的,f()函数在n小于等于1时返回1,而在其余情况下返回n*f(n-2)。所以本题的递归算法可以表示为: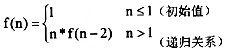
题目要求的结果是f(5),即f(5)=5*f(3)=5*3*f(1)=5*3*1=15。故应该填15。 -
第22题:
递归函数f(n)=f(n-1)+n(n>1)的递归出口是()
- A、 f(1)=0
- B、 f(1)=1
- C、 f(0)=1
- D、 f(n)=n
正确答案:B -
第23题:
单选题设有一个递归算法如下: int fact(int n) { //n大于等于0 if(n<=0) return 1; else return n*fact(n-1); } 则计算fact(n)需要调用该函数的次数为()An+1
Bn-1
Cn
Dn+2
正确答案: A解析: 特殊值法。设n=0,易知仅调用一次fact(n)函数,故选A。
