I=∮C|y|ds的值为下列( )项，其中C：(x2+y2)2=a2(x2-y2)，a＞0。

题目
I=∮C|y|ds的值为下列( )项，其中C：(x2+y2)2=a2(x2-y2)，a＞0。


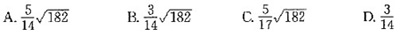
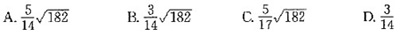
相似考题

1.设平面薄板所占xOy平面上的区域D为1≤x2+y2≤4，*≥0，y≥0，其面密度为π(x，y)=x2+y2，求该薄板的质量m。

2.I=∮C|y|ds的值为下列( )项，其中C：(x2+y2)2=a2(x2-y2)，a＞0。

3. 是由曲面z=x2+y2，y=x，y=0，z=1在第一

4.设z=f（x2－y2），则dz 等于： A. 2x－2y B. 2xdx－2ydy C. f’（x2－y2）dx D.2f’（x2－y2）（xdx—ydy）

参考答案和解析
答案：D
解析：
曲线C可采用极坐标方程形式，然后根据曲线C及被积函数|y|关于x轴、y轴的对称性可得解
更多“I=∮C|y|ds的值为下列( )项，其中C：(x2+y2)2=a2(x2-y2)，a＞0。 ”相关问题

  • 第1题：

    设z=f(x2-y2)，则dz 等于：
    A. 2x-2y B. 2xdx-2ydy
    C. f'(x2-y2)dx D. 2f'(x2-y2)(xdx-ydy)


    答案：D
    解析：
    提示:本题为二元函数求全微分的题目，计算公式为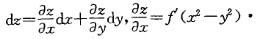

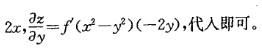
  • 第2题：

    圆x2＋y2＝25上的点到直线5x＋12y－169＝0的距离的最小值是（　　）

    A.9
    B.8
    C.7
    D.6

    答案：B
    解析：

  • 第3题：

    计算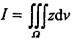,其中Ω为z2=x2+y2，z=1所围成的立体，则正确的解法是( )。


    答案：B
    解析：
    提示：在柱坐标下计算

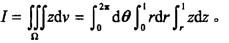
  • 第4题：

    设平面薄板所占Oxy平面上的区域D为1≤x2+y2≤4，x≥0，y≥0，其面密度
    u(x，y)=2+y2，求该薄板的质量m．


    答案：
    解析：
    由二重积分物理意义知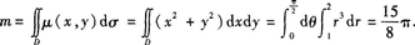
    【评析】如果被积函数为f(x2+y2)的形式，积分区域D为圆域或圆的一部分，此时将
    化为极坐标计算常常较简便．

  • 第5题：

    设C为圆周x2+y2=ax（a>0），则曲线积分的值是（）．

    • A、a2
    • B、2a2
    • C、3a2
    • D、4a2

    正确答案:B

  • 第6题：

    填空题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

    正确答案： -1/7
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第7题：

    单选题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
    A

    1/5

    B

    1/7

    C

    －1/7

    D

    －1/5


    正确答案： B
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第8题：

    单选题
    ∫L（x2＋y2＋2x）ds＝（　　），其中曲线L为x2＋y2＝R2
    A

    πR3

    B

    2πR3

    C

    4πR3

    D

    6πR3


    正确答案： D
    解析：
    由曲线方程L为x2＋y2＝R2可知曲线关于y轴对称，且函数2x是x的奇函数，故∫L2xds＝0。故∫L（x2＋y2＋2x）ds＝∫L（x2＋y2）ds＝∫LR2ds＝R22πR＝2πR3。

  • 第9题：

    单选题
    已知流速场ux＝ax，uy＝－ay，uz＝0，求流函数ψ（　　）。
    A

    无ψ

    B

    ψ＝a（x2－y2）

    C

    ψ＝a（x2＋y2）

    D

    ψ＝axy


    正确答案： D
    解析：
    流函数与速度场的关系式为：ψ＝∫uxdy－uydx。因此流函数ψ＝∫axdy＋aydx＝axy＋C。取常数C＝0，则ψ＝axy。

  • 第10题：

    单选题
    设z＝φ（x2－y2），其中φ有连续导数，则函数z满足（　　）。
    A

    x∂z/∂x＋y∂z/∂y＝0

    B

    x∂z/∂x－y∂z/∂y＝0

    C

    y∂z/∂x＋x∂z/∂y＝0

    D

    y∂z/∂x－x∂z/∂y＝0


    正确答案： D
    解析：
    令u＝x2－y2，则z＝φ（u），∂z/∂x＝φ′（u）·2x＝2xφ′（u），∂z/∂y＝－2yφ′（u），故y∂z/∂x＋x∂z/∂y＝0。

  • 第11题：

    单选题
    I＝∮L（－ydx＋xdy）/（x2＋y2），因为∂Q/∂x＝∂P/∂y＝（y2－x2）/（x2＋y2）2，所以（　　）。
    A

    对任意闭曲线L，I＝0

    B

    在L为不含原点在内的闭区域的边界线时I＝0

    C

    因为∂Q/∂x＝∂P/∂y在原点不存在，故对任意L，I≠0

    D

    在L含原点在内时I＝0，不含原点时I≠0


    正确答案： A
    解析：
    考察对于格林公式的使用条件的应用。在题设中，有∂Q/∂x＝∂P/∂y，但当原点在L内时，由于P、Q不满足在单连通域内有一阶连续偏导数的条件，故只有原点在D外时，曲线积分才与路径无关，此时I＝0。

  • 第12题：

    问答题
    设z＝f（x2－y2，exy），其中f具有连续二阶偏导数，求∂z/∂x，∂z/∂y。

    正确答案：
    由复合函数的求导法则,得∂z/∂x=2xf1′+yexyf2′,∂z/∂y=-2yf1′+xexyf2′。
    解析： 暂无解析

  • 第13题：

    (其中D:x2+y2≤1)化为极坐标系下的二次积分，其形式为下列哪一式？


    答案：D
    解析：
    提示:化为极坐标系下的二次积分，面积元素dσ=rdrdθ，把x=rcosθ，y=rsinθ代入。

  • 第14题：

    设z=f(x2-y2)，则dz 等于：

    A. 2x-2y
    B. 2xdx-2ydy
    C. f'(x2-y2)dx
    D. 2f'(x2-y2)(xdx-ydy)

    答案：D
    解析：

  • 第15题：

    将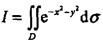 (其中D：x2+y2≤1)化为极坐标系下的二次积分，其形式为( )。


    答案：D
    解析：
    提示：。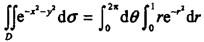

  • 第16题：

    已知X1=+0010100，Y1=+0100001，X2=0010100，Y2=0100001，试计算下列各式（设字长为8位）。 （1）[X1＋Y1]补=[X1]补＋[Y1]补=（） （2）[X1－Y2]补=[X1]补＋[－Y2]补=（） （3）[X2－Y2]补=[X2]补＋[－Y2]补=（） （4）[X2＋Y2]补=[X2]补＋[Y2]补=（）


    正确答案:00010100＋00100001=00110101；00010100＋00100001=00110101；11101100＋00100001=00001101；11101100＋11011111=11001011

  • 第17题：

    设z=f（x2+y2），其中f具有二阶导数，则等于（）．

    • A、2f’（x2+y2）
    • B、4x2f"（x2+y2）
    • C、2’（x2+y2）+4x2f"（x2+y2）
    • D、2xf"（x2+y2）

    正确答案:C

  • 第18题：

    单选题
    与一族曲线中的每一条都交成直角的曲线叫做所给曲线族的正交轨线，若曲线族为x2＋y2＝2cx（c为常数），则此曲线族的正交轨线为（　　）。
    A

    y＝c1（x2＋y2）

    B

    y＝c1（x＋y）

    C

    y＝2c1（x2＋y2）

    D

    y＝c1（x2＋y2）/2


    正确答案： C
    解析：
    已知曲线族方程为x2＋y2＝2cx，方程两边对x求导得2x＋2y·yx′＝2c。由以上两式可得y′＝（y2－x2）/（2xy），即正交轨线的方程应满足y′＝2xy/（x2－y2），解此微分方程得y＝c1（x2＋y2）。

  • 第19题：

    单选题
    设z=f（x2+y2），其中f具有二阶导数，则等于（）．
    A

    2f’（x2+y2）

    B

    4x2f（x2+y2）

    C

    2’（x2+y2）+4x2f（x2+y2）

    D

    2xf（x2+y2）


    正确答案： D
    解析： 暂无解析

  • 第20题：

    单选题
    ∫L（x2＋y2＋2x）ds＝（　　），其中曲线L为x2＋y2＝R2
    A

    2πR3/3

    B

    2πR3

    C

    4πR3

    D

    πR3


    正确答案： A
    解析：
    由曲线方程L为x2＋y2＝R2可知曲线关于y轴对称，且函数2x是x的奇函数，故∫L2xds＝0。故∫L（x2＋y2＋2x）ds＝∫L（x2＋y2）ds＝∫LR2ds＝R22πR＝2πR3。

  • 第21题：

    单选题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
    A

    1

    B

    －1

    C

    1/7

    D

    －1/7


    正确答案： B
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第22题：

    单选题
    设C为圆周x2+y2=ax（a>0），则曲线积分的值是（）．
    A

    a2

    B

    2a2

    C

    3a2

    D

    4a2


    正确答案： B
    解析： 暂无解析

  • 第23题：

    填空题
    ∫L（x2＋y2＋2x）ds＝____，其中曲线L为x2＋y2＝R2

    正确答案： 2πR3
    解析：
    由曲线方程L为x2＋y2＝R2可知曲线关于y轴对称，且函数2x是x的奇函数，故∫L2xds＝0。故∫L（x2＋y2＋2x）ds＝∫L（x2＋y2）ds＝∫LR2ds＝R22πR＝2πR3。

  • 第24题：

    单选题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
    A

    －1/2

    B

    －1/4

    C

    －1/7

    D

    －1/9


    正确答案： C
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

相关内容