A与B都是3×2矩阵,则A与B的乘积也是3×2矩阵。()此题为判断题(对，错)。
题目
此题为判断题(对，错)。
相似考题
更多“A与B都是3×2矩阵,则A与B的乘积也是3×2矩阵。() 此题为判断题(对，错)。”相关问题
-
第1题：
组织结构中最传统也是最常见的形式是矩阵型组织。()此题为判断题(对，错)。
参考答案：×
-
第2题：
既能与上三角矩阵可交换又能与下矩阵较换则这个矩阵一定是对角矩阵。()此题为判断题(对，错)。
参考答案：正确
-
第3题：
既能与上三角矩阵可交换又能与下矩阵交换则这个矩阵一定是对角矩阵。()此题为判断题(对，错)。
参考答案：对
-
第4题：
n阶单位矩阵的特征值都是1。()此题为判断题(对，错)。
参考答案：正确
-
第5题：
若矩阵A可逆,则AB与BA相似。()此题为判断题(对，错)。
参考答案：正确
-
第6题：
设直接消耗系数矩阵为A,I为单位阵,则完全消耗系数矩阵B=(I－A)－1()此题为判断题(对，错)。
正确答案：错误
-
第7题：
设A为2×4矩阵,B为3×5矩阵,且乘积矩阵ACB^T有意义,则C^T为()矩阵。A.4×5
B.5×4
C.3×2
D.2×3
正确答案：B
-
第8题：
总体刚度矩阵是结构体节点向量与节点力向量之间的关系矩阵。()此题为判断题(对，错)。
正确答案:正确
-
第9题：
设为3阶矩阵，将的第2列加到第1列得矩阵，再交换的第2行与第3行得单位矩阵，记，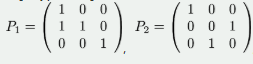
，则A=（ ）
答案：D解析：
-
第10题：
设矩阵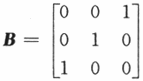
，已知矩阵A相似于B，则秩(A-2E)与秩(A-E)之和等于A.2
B.3
C.4
D.5答案：C解析：
-
第11题：
有4个矩阵{A1，A2，A3，A4}，其中Ai与Ai＋1是可乘的，i=1，2，3，连乘积为A1A2A3A4。在这个四矩阵连乘积问题中，请问不同子问题的个数总共有多少个，并请把所有的子问题列出来。
正确答案: 5个
（A1（A2（A3A4）））
（A1（（A2A3）A4））
（（A1A2）（A3A4））
（（A1（A2A3））A4）
（（（A1A2）A3）A4） -
第12题：
判断题索引矩阵经2次过乘幂法则后得到的矩阵I^3，其描述的还是原系统中3步弧的信息，与Berge定理意义相同A对
B错
正确答案： 错解析： 暂无解析 -
第13题：
通用矩阵与波士顿矩阵是截然不同的两种用于业务组合分析的方法。 ()此题为判断题(对，错)。
正确答案：错误
-
第14题：
两个行列式相等的正交矩阵的乘积也是正交矩阵。()此题为判断题(对，错)。
参考答案：错
-
第15题：
设6阶方阵A的秩为3,则其伴随矩阵的秩也是3。()此题为判断题(对，错)。
参考答案：错误
-
第16题：
设二阶矩阵A与B相似,A的特征值为－1,2,则|B|=1。()此题为判断题(对，错)。
参考答案：错误
-
第17题：
已知矩阵A3×2,B2×3,C3×3,则A*B为3×3矩阵。()此题为判断题(对，错)。
参考答案：正确
-
第18题：
矩阵分析方法包括波士顿矩阵和GE矩阵。()此题为判断题(对，错)。
参考答案：正确
-
第19题：
雅可比矩阵是对称矩阵。()此题为判断题(对，错)。
正确答案：错误
-
第20题：
设A是3阶矩阵，P=(a1,a2,a3)是3阶可逆矩阵，
若矩阵Q=(a1,a2,a3)，则Q-1AQ=
答案：B解析：提示:当P-1AP=Λ时，P=(a1,a2,a3)中a1,a2,a3的排列满足对应关系，a1对应λ1，a2对应λ2，a3对应λ3，可知a1对应特征值λ1=1，a2对应特征值λ2=2，a3对应特征值λ3=0，由此可
-
第21题：
设A与B都是n阶正交矩阵，证明AB也是正交矩阵.答案：解析：
-
第22题：
设A是3阶矩阵，P = (α1，α2，α3)是3阶可逆矩阵，且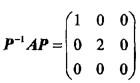
，若矩阵Q=(α2，α1，α3),则Q-1AQ=( )。
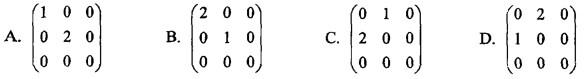答案：B解析：提示：由条件知，λ1=1，λ2=2，λ3=0是矩阵A的特征值,而α1，α2，α3是对应的特征向量，故有
。 -
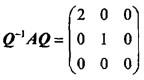第23题：
问答题有4个矩阵{A1，A2，A3，A4}，其中Ai与Ai＋1是可乘的，i=1，2，3，连乘积为A1A2A3A4。在这个四矩阵连乘积问题中，请问不同子问题的个数总共有多少个，并请把所有的子问题列出来。正确答案： 5个
（A1（A2（A3A4）））
（A1（（A2A3）A4））
（（A1A2）（A3A4））
（（A1（A2A3））A4）
（（（A1A2）A3）A4）解析： 暂无解析