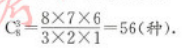将四个颜色互不相同的球全部放人编号为1和2的两个盒子里，使得放入每个盒子里球的个数不小于盒子的编号，则不同的放球方法有（ ）种。 A．9 B．10 C．12 D．18

题目

将四个颜色互不相同的球全部放人编号为1和2的两个盒子里，使得放入每个盒子里球的个数不小于盒子的编号，则不同的放球方法有（ ）种。 A．9 B．10 C．12 D．18

相似考题

1.现在将编号为1、2、3、4、5、6的6个球分别放入编号为1、2、3、4、5、6的6个盒子里，每个盒子放1个球。请问。恰好有2个盒子编号与球编号一样的投放方法有多少种? A．15 B．24 C．135 D．270

2.将四个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里球的个数不小于盒子的编号，则不同的放球方法有（ ）种。A．9B．10C．12D．18

3.现在将编号为1、2、3、4、5、6的6个球分别放入编号为1、2、3、4、5、6的6个盒子里，每个盒子放1个球。请问，恰好有2个盒子编号与球编号一样的投放方法有多少种?A．15B．24C．135D．270

4.将12个球放入3个盒子里，使每个盒子里球的数目是偶数，且没有空盒，问共有几种放法?（ ）A．10B．12C．8D．6

更多“将四个颜色互不相同的球全部放人编号为1和2的两个盒子里,使得放入每个盒子里球的个数不小于盒子 ”相关问题

  • 第1题：

    现在将编号为1、2、3、4、5、6的6个球分别放入编号为1、2、3、4、5、6的6个盒子里，每个盒子放1个球。请问，恰好有2个盒子编号与球编号一样的投放方法有多少种？

    A.15
    B.24
    C.135
    D.270

    答案：C
    解析：
    首先选出2个编号和球一样的盒子，有种方法；剩余的4个再进行错位重排，有3x3=9种方法。因此一共有15x9=135种方法。

  • 第2题：

    设有编号为1,2,3,4,5的5个球和编号为1,2,3,4,5的5个盒子,将5个小球放入5个盒子中（每个盒子中放入1个小球）,则至少有2个小球和盒子编号相同的方法有（ ）

    A.36种
    B.49种
    C.31种
    D.28种
    E.72种

    答案：C
    解析：

  • 第3题：

    现有n个盒子，若每2个盒子里都恰有1个相同颜色的球，每种颜色的球恰好有2个，并放在不同盒子里，请问这n个盒子里的球共有多少种不同的颜色？

    A．n / 2

    B．n

    C．n(n-1) / 2

    D．n(n-1)


    n (n-1) / 2

  • 第4题：

    三个相同的盒子里各有2个球，其中一个盒子里放了2个红球，一个盒子里放了2个蓝球，一个盒子里放了红球和蓝球各1个。随机选择一个盒子后从中随机摸出一球是红球，则这个盒子里另一个球是红球的概率为（ ）。

    A.1/2
    B.3/4
    C.2/3
    D.4/5

    答案：C
    解析：

  • 第5题：

    若将15只相同的球随机放入编号为1,2,3,4的四个盒子中,每个盒子中小球的数目,不少于盒子的编号,则不同的投放方法有（ ）种

    A.56
    B.84
    C.96
    D.108
    E.120

    答案：A
    解析：
    减少元素法,第一步:先将1,2,3,4四个盒子分别放0,1,2、3个球,因为球是相同的球,故只有一种放法.第二步:余下的9个球放入四个盒子、则毎个盒子至少放一个,使用挡法,即

相关内容