有l0名选手参加一次棋类比赛，每个人都要和其他选手赛一盘，共要赛多少盘?（ ）。A．45B．46C．47D．48

题目

有l0名选手参加一次棋类比赛，每个人都要和其他选手赛一盘，共要赛多少盘?（ ）。

A．45

B．46

C．47

D．48

相似考题

1.有A、B、C、D、E五位同学一起比赛象棋，每两人之间只比赛一盘，统计比赛的盘数知：A赛了4盘，B赛了3盘，C赛了2盘，D赛了1盘。则同学E赛的盘数是（ ）。A．1盘B．2盘C．3盘D．4盘

2.一次象棋比赛共有10名选手参加，他们分别来自甲、乙、丙三个队，每个人都与其余九名选手各赛一盘，每盘棋的胜利者得1分，负者得0分，平局各得0.5分。结果甲队选手平均得4.5分，乙队选手平均得3.6分，丙队选手平均得9分，那么甲、乙、丙三队参加比赛的选手的人数依次是（ ）。A. 6人、3人、1人B.4人、5人、1人C. 3人、5人、2人D.5人、1人、4人

3.有A、B、C、D、E五位同学一起比赛象棋，每两人之间只比赛一盘，统计比赛的盘数知：A赛了4盘，B赛了3盘，C赛了2盘，D赛了1盘，则同学E赛的盘数是( )。A.1盘 B.2盘 C.3盘 D.4盘

4.：有l0名选手参加一次棋类比赛，每个人都要和其他选手赛一盘，共要赛多少盘?（ ）。A．45B．46C．47D．48

更多“有l0名选手参加一次棋类比赛,每个人都要和其他选手赛一盘,共要赛多少盘?( )。 A.45 ”相关问题

  • 第1题：

    某单位职员在健身活动中举行乒乓球比赛，每个选手都要和其他选手各赛一场，一共120场比赛，则该单位参加人数是( )人。

    A.18

    B.16

    C.15

    D.14


    正确答案：B

    略

  • 第2题：

    一次国际象棋比赛，有10名选手参加，每名选手都要与其他选手比赛一次，选手们的得分全不一样。已知：
    (1)第一名选手和第二名选手一次都没有输；
    (2)前两名的总分比第三名选手多10分；
    (3)第四名选手与最后四名选手的得分和相等。
    (每局棋胜者得1分，负者得0分，平局每人得0. 5分）
    请问:从第一名到第六名共得分数为（）。
    A. 46 B. 25 C. 18 D. 39


    答案：D
    解析：
    单循环赛，每人赛9盘棋，所以最高分为9分，前两名都没有输，说明没有全胜的人。所以，最高分最多为8. 5分。
    那么，第二名最多8分，第三名最多8.5+8-10 = 6. 5（分），第四名最多6分。
    后四名选手之间要赛4X3 /2=6（盘）。
    每盘出现1分，这四人之间要累计6分，那么这四人的总分至少要有6分，就是说第四名的分数至少是6分。
    综合“第四名最多6分”“第四名的分数至少是6分”，可知第四名的得分应该是6分。
    由此可知：第三名6. 5分，第四名6分，第一名是8. 5分，第二名是8分，后四人最后总分是6分。
    10名选手的循环赛总盘数是1/2x10x(10-1)=45(盘)，总分是1x45 = 45(分)。故第一到第六名共得的分数为45-6=39(分)。所以本题选D。

  • 第3题：

    5.在有n个选手参加的单循环赛中，总共将进行（）场比赛。


    n(n-1)/2__

  • 第4题：

    某单位职员在健身活动中举行乒乓球比赛，每个选手都要和其他选手各赛一场，一共120场比赛，则该单位参加人数是（ ）人。

    A.18
    B.16
    C.15
    D.14

    答案：B
    解析：
    本题考查的是排列组合知识。假设总共有X人，因为每两个人要进行一场比赛，所以应该用组合公式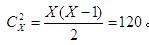： 。此时利用代入排除法，只有X=16时满足条件。故正确答案为B。

  • 第5题：

    .有A、B、C、D、E五位同学一起比赛象棋，每两人之间只比赛一盘，统计比赛的盘数知：A赛了4盘，B赛了3盘，C赛了2盘，D赛了1盘，则同学E赛的盘数是（　　）。

    A.1盘
    B.2盘
    C.3盘
    D.4盘

    答案：B
    解析：
    由题意首先可知A与B、C、D、E均比赛过。那么D只赛了的一盘应是与A进行的。已知B与A比赛过一盘，则另两盘应是与C、E进行的。由以上推理可知C比赛过的两盘应是与A、B进行的。所以E只与A、B比赛过。正确答案为B。

相关内容