:学校举办一次中国象棋比赛,有10 名同学参加,比赛采用单循环赛制,每名同学都要与其他9 名同学比赛一局.比赛规则,每局棋胜者得2 分, 负者得O 分,平局两人各得l 分.比赛结束后,10 名同学的得分各不相同,已知:( 1 )比赛第一名与第二名都是一局都没有输过; ( 2 ) 前两名的得分总和比第三名多20 分;( 3 )第四名的得分与最后四名的得分和相等.那么,排名第五名的同学的得分是:A . 8 分B . 9 分C . 10 分D . 11 分
题目
:学校举办一次中国象棋比赛,有10 名同学参加,比赛采用单循环赛制,每名同学都要与其他9 名同学比赛一局.比赛规则,每局棋胜者得2 分, 负者得O 分,平局两人各得l 分.比赛结束后,10 名同学的得分各不相同,已知:( 1 )比赛第一名与第二名都是一局都没有输过; ( 2 ) 前两名的得分总和比第三名多20 分;( 3 )第四名的得分与最后四名的得分和相等.那么,排名第五名的同学的得分是:
A . 8 分
B . 9 分
C . 10 分
D . 11 分
相似考题
参考答案和解析
这个题目比较复杂,条件多。包括一些专家给出的答案,也不一致。众说纷纭。
首先,要明白每场比赛产生的分值是2分。
其次要明白比赛一共进行了45场。因此产生的分数总值是90分。
第三,个人选手的最高分只能是18分,假设9场比赛全部赢。根据( 1 )比赛第一名与第二名都是一局都没有输过,可以得出第一名一定和棋过。要是第一名全部赢了,那么第二名一定输过棋。这说明第一名最多17分,第二名最多16分。
条件一:
第一名和第二名的总分最多33分。
当他们的总分是33时,第三名分数为13分。假设第四名为12分,第7,8。9。10。名的分数和为12分。第五名为11分,第六名分数为9分。
当他们的总分是33时,第三名分数为13分。如果假设第四名为11分,那么第7,8。9。10。名的分数和为11分。第五六名的分数和为22分。必定有人分数高于11分,矛盾。在条件一下,其他任意假设也推导出矛盾来。
条件二:
第一名和第二名总分为32分时,第三名为12分。第四名最多为11分。 那么第7,8。9。10。名的分数和为11分。第五名和第六名分数和为24分。结果推导出矛盾来。
其他条件都会推导出矛盾来。
因此,第五名的成绩是11分。
更多“:学校举办一次中国象棋比赛,有10 名同学参加,比赛采用单循环赛制,每名同学都要与其他9 名 ”相关问题
-
第1题:
:学校举办一次中国象棋比赛,有10名同学参加,比赛采用单循环赛制,每名同学都要与其他9名同学比赛一局。比赛规则,每局棋胜者得2分,负者得0分,平局两人各得1分。比赛结束后,10名同学的得分各不相同,已知: (1)比赛第一名与第二名都是一局都没有输过; (2)前两名的得分总和比第三名多20分; (3)第四名的得分与最后四名的得分相等。 那么,排名第五名的同学的得分是( )。
A. 8分
B. 9分
C.10分
D.11分
正确答案:D本题运用代入法,经计算正确答案为D。
-
第2题:
某单位组织的羽毛球男单比赛共有48名选手报名参加,比赛采用淘汰赛制,在比赛中负一场的选手即被淘汰,直至决出最后的冠军。如每名选手每天最多参加一场比赛,则比赛至少需要举行几天?A.4
B.5
C.6
D.7答案:C解析:根据题意,每一轮的比赛都安排在一天,48=2 4 3,则4天后还剩3名选手,这3名选手还需要两场比赛才能决出冠军,所以比赛至少要举行4+2=6天。 -
第3题:
学校举办一次中国象棋比赛,有10名同学参加,比赛采用单循环赛制,每名同学都要与其他9名同学比赛一局。比赛规则,每局棋胜者得2分,负者得0分,平局两人各得1分。比赛结束后,10名同学的得分各不相同,已知:
(1)比赛第一名与第二名都是一局都没有输过;
(2)前两名的得分总和比第三名多20分;
(3)第四名的得分与最后四名的得分和相等。
那么,排名第五名的同学的得分是( )。
A. 8分
B. 9分
C.10分
D.11分答案:D解析:【参考解析】: 本题运用代入法,经计算正确答案为D。 -
第4题:
某次足球比赛,共有来自全国各地的10支球队参加,比赛采用单循环赛制,每队都要跟其他九队比赛一次,胜者计2分,败者计0分,平局则各计1分。赛后,各队得分各不相同,第一名和第二名都没有输过,他们的得分总和比第三名多20分,第四名得分与最后四名的得分之和相等。那么,第五名的球队得分是多少? ( )A.10
B.11
C.12
D.13答案:B解析:根据题意,共有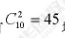
场比赛,每场比赛总得分2分(分胜负2+0,平局1+1),总得分为90分。如果第-名和第二名都没有输过,则第一和第二之间肯定是平局,
每队比赛9场,故第一名最多可得17分(8胜1平),第二名最多可得16分(比第一名少1分),第三名最多13分,第4名最多12分,那么7、8、9、10名得分之和为12分,列方程: 17+16+13+12+12+第五名+第六名-90分, 可得,第五名+第六名=20分,又因为得分各不相同,第五名得分为11分,满足题意。
-
第5题:
某学校召开春季田径运动会,甲同学报名参加100米跑和跳远比赛,可当准备参加跳远比赛时,100米跑比赛也即将开始,甲同学不知道应该先参加哪项比赛,就找裁判长问:“王老师,我先参加哪项呀?”王老师刚要回答,又有乙同学来问:“老师,我的跳高成绩和第一名的跳高成绩都是1.68米,为什么我是第二名呢?”王老师根据规则,分别做了解答。
关于甲同学的兼项问题怎么处理?答案:解析:如果一名运动员参加一个径赛项目,同时又参加一个田赛项目,或者参加一个以上的田赛项目,而这些项目又同时举行比赛时,有关主裁判可以允许运动员只在某一轮次(高度项目以一个高度为一个轮次,一个高度有三次试跳机会;远度项目以所有运动员按顺序试跳或试掷完一次为一个轮次)的比赛中以不同于赛前抽签确定的顺序先进行试跳(试掷)一次。回来后已错过的试跳(试掷)顺序一律不补。
