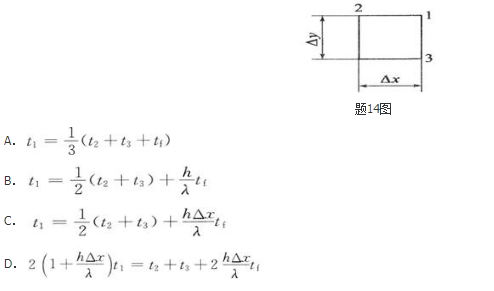
常物性无内热源二维稳态导热过程，在均匀网格步长下，Δx=Δy如图所示的拐角节点1处于第三类边界条件时，其差分格式为（　　）。

题目
常物性无内热源二维稳态导热过程，在均匀网格步长下，Δx=Δy如图所示的拐角节点1处于第三类边界条件时，其差分格式为（　　）。

相似考题

1.物性参数为常数的一圆柱导线,通过的电流均匀发热,导线与空气间的表面传热系数为定值,建立导线的导热微分方程采用()。A、柱坐标下一维无内热源的不稳态导热微分热方程B、柱坐标下一维无内热源的稳态导热微分热方程C、柱坐标下一维有内热源的不稳态导热微分热方程D、柱坐标下一维有内热源的稳态导热微分热方程

2.当热力设备长时间处于稳定运行状态时,其部件内发生的导热过程为稳态导热。()此题为判断题(对，错)。

3.对于题13图中的二维稳态导热问题，右边界是恒定热流边界条件，热流密度为qw，若采用有限差分法求解，当Δx＝Δy时，则在下面的边界节点方程式中正确的是（　　）。

4.一维非稳态导热采用向前差分离散微分方程，其显式格式的中心节点方程的稳定性条件为( )。A．Fo＜1/2B．Fo≤1/2C．Fo≥1/2D．Fo＞1/2A．B．C．D．

参考答案和解析
答案：D
解析：
第三类边界条件：已知壁面相邻流体温度和表面传热系数。本题图示拐角节点1所代表的微元体为四分之一网格，由热平衡关系式列节点1的平衡方程：
更多“常物性无内热源二维稳态导热过程，在均匀网格步长下，Δx=Δy如图所示的拐角节点1处于第三类边界条件时，其差分格式为（　　）。”相关问题

  • 第1题：

    第一类边界条件下，常物性稳态导热大平壁，其温度分布与导热系数无关的条件是( )。

    A.无内热源
    B.内热源为定值
    C.负内热源
    D.正内热源

    答案：A
    解析：

  • 第2题：

    单层圆柱体内一维径向稳态导热过程中，无内热源，物性参数为常数，则下列说法正确的是( )。

    A.导热量Φ为常数
    B.导热量Φ为半径的函数
    C.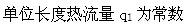
    D.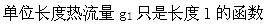

    答案：C
    解析：

  • 第3题：

    常物性无内热源一维非稳态导热过程第三类边界条件下微分得到离散方程，进行计算时要达到收敛需满足( )。

    A.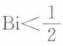
    B.Fo≤1
    C.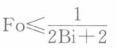
    D.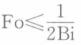

    答案：C
    解析：

  • 第4题：

    在稳态常物性无内热源的导热过程中，可以得出与导热率（导热系数）无关的温度分布通解，t＝ax＋b，其具有特性为（　　）。

    A． 温度梯度与热导率成反比
    B． 导热过程与材料传导性能无关
    C． 热量计算也与热导率无关
    D． 边界条件不受物理性质影响

    答案：D
    解析：

  • 第5题：

    如图所示，有一长圆柱，两端温度是t0，其导热系数为λ，圆柱的外柱周围是完全绝热的，圆柱内部具有热流强度为qv的均匀内热源。正确描述这圆柱内稳态温度分布的微分方程式（　　）。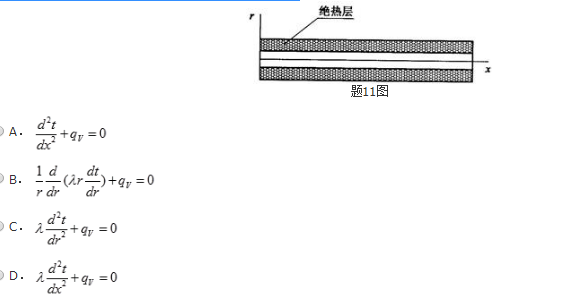


    答案：B
    解析：

  • 第6题：

    单层圆柱体内径一维径向稳态导热过程中无内热源，物性参数为常数，则下列说法正确的是（　　）。

    A． φ导热量为常数
    B． φ为半径的函数
    C． q1（热流量）为常数
    D． q1只是l的函数

    答案：C
    解析：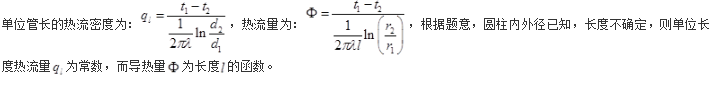

  • 第7题：

    单层圆柱体内径一维径向稳态导热过程中无内热源，物性参数为常数，则下列说法正确的是( )。

    A.Φ导热量为常数
    B.Φ为半径的函数
    C.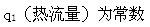
    D.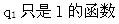

    答案：C
    解析：
    Φ为圆柱体高的函数。

  • 第8题：

    在稳态、常物性、无内热源的导热物体中，最低温度出现在（）

    • A、内部某一点
    • B、形心
    • C、质心
    • D、边界上

    正确答案:D

  • 第9题：

    非稳态一维导热过程采用显式差分法格式计算时，时间步长和空间步长之间要满足（）

    • A、Fo<0.5；
    • B、Fo>1；
    • C、Bi<0.1；
    • D、Fo<0.25。

    正确答案:A

  • 第10题：

    有人对二维矩形物体中的稳态无内热源常物性的导热问题进行了数值计算。矩形的一个边绝热，其余三个边均与温度为tf的流体发生对流换热。你能预测他所得的温度场的解吗？


    正确答案:能，因为在一边绝热其余三边为相同边界条件时，矩形物体内部的温度分布应为关于绝热边的中心线对称分布。

  • 第11题：

    单选题
    在稳态常物性无内热源的导热过程中，可以得出与导热率（导热系数）无关的温度分布通解，t＝ax＋b，其具有特性为（　　）。[2018年真题]
    A

    温度梯度与热导率成反比

    B

    导热过程与材料传导性能无关

    C

    热量计算也与热导率无关

    D

    边界条件不受物理性质影响


    正确答案： C
    解析：
    A项，由于gradt(→)＝（∂t/∂n）n(→)，t＝ax＋b，因此温度梯度gradt(→)与热导率λ无关。BC两项，q(→)＝－λgradt(→)＝－λ（∂t/∂n）n(→)，因此导热过程除了与温度场有关，还与热导率λ有关。影响导热系数λ的主要因素是物质的种类和温度。D项，边界条件受外界换热环境影响，而不受物理性质的影响。

  • 第12题：

    问答题
    有人对二维矩形物体中的稳态无内热源常物性的导热问题进行了数值计算。矩形的一个边绝热，其余三个边均与温度为tf的流体发生对流换热。你能预测他所得的温度场的解吗？

    正确答案： 能，因为在一边绝热其余三边为相同边界条件时，矩形物体内部的温度分布应为关于绝热边的中心线对称分布。
    解析： 暂无解析

  • 第13题：

    常物性有内热源（qc＝C，W/m3）二维稳态导热过程，在均匀网格步长下，如图所示，其内节点差分方程可写为（　　）。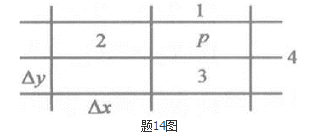

    A． tp＝（t1＋t2＋t3＋qv/λ）/4
    B． tp＝（t1＋t2＋t3＋t4）/4＋qvΔx2/（4λ）
    C． tp＝（t1＋t2＋t3＋t4）/4＋qvΔx2
    D． tp＝（t1＋t2＋t3＋t4）/4

    答案：B
    解析：
    建立热平衡关系式：λ?x（t1－tp）/?x＋λ?x（t2－tp）/?x＋λ?x（t3－tp）/?x＋λ?x（t4－tp）/?x＋qv?x2＝0。解得：tp＝（t1＋t2＋t3＋t4）/4＋qv?x2/（4λ）。

  • 第14题：

    对于一维非稳态导热的有限差分方程，如果对时间域采用显式格式进行计算，则对于内部节点而言，保证计算稳定性的判据为( )。

    A.Fo≤1
    B.Fo≥1
    C.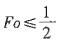
    D.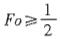

    答案：C
    解析：

  • 第15题：

    常物性无内热源二维稳态导热过程，在均匀网格步长下，如图所示的平壁面节点处于第二类边界条件时，其差分格式为（　　）。



    答案：D
    解析：
    节点1为边界节点，其节点方程为：

    本题选项都是错误的，答案中无正确选项，其中较为接近的是D选项。

  • 第16题：

    对于一维非稳态导热的有限差分方程，如果对时间域采用显式格式进行计算，则对于内部节点而言，保证计算稳定性的判据为（　　）。

    A． Fo≤1
    B． Fo≥1
    C． Fo≤1／2
    D． Fo≥1／2

    答案：C
    解析：
    对非稳态导热的显式格式，其数值解的稳定性要受到稳定性条件的限制。对于内部节点的稳定性条件是：Fo≤1/2；对于第三类边界条件的稳定性条件是：

  • 第17题：

    物性参数为常数的一圆柱导线，通过的电流均匀发热，导线与空气间的表面传热系数为定值，建立导线的导热微分方程采用( )。

    A.柱坐标下一维无内热源的不稳态导热微分方程
    B.柱坐标下一维无内热源的稳态导热微分方程
    C.柱坐标下一维有内热源的不稳态导热微分方程
    D.柱坐标下一维有内热源的稳态导热微分方程

    答案：D
    解析：
    圆柱导线，沿长度方向电流均匀发热，热量沿半径方向从里向外传递，因此应建立柱坐标下一维(沿半径方向)有内热源的稳态导热微分方程。

  • 第18题：

    对于图中的二维稳态导热问题，右边界是恒定热流边界条件，热流密度为qw，如果采用有限差分法求解，当Δx=Δy时，则在下面的边界节点方程式中，哪一个是正确的？（　　）


    答案：D
    解析：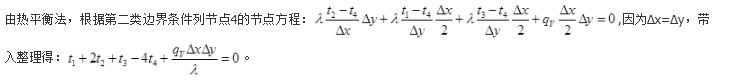

  • 第19题：

    对于题12图中二维稳态导热问题，右边界是绝热的。如果采用有限差分法求解，当Δx＝Δy时，则正确的边界节点方程是（　　）。


    答案：B
    解析：
    边界节点离散方程在第一类边界条件下，因边界节点的温度已给定，无需建立边界节点的方程，其温度值会进入到与之相邻的内节点方程中。对于第二及第三类边界条件，则必须建立边界节点的节点方程，从而使整个节点方程组封闭，利于求解。则根据图2列节点4的热平衡方程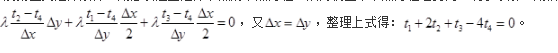

  • 第20题：

    对于二维稳态导热过程，如果物性参数为常数，t1、t2、t3和t4分别为四周四点温度，t5为中心节点温度，则均匀网格有限差分的内部节点方程（）

    • A、t1+t2+t3+t4-t5=0；
    • B、t1+t2+t3+t4-4t5=0；
    • C、t1+t2+t3+t4-6t5=0；
    • D、t1+t2+t3+t4-2t5=0

    正确答案:B

  • 第21题：

    某一稳态、常物性、无内热源的导热物体的表面最低温度为100℃，那么其内部绝对不可能出现的温度是（）

    • A、50℃
    • B、200℃
    • C、1000℃
    • D、2000℃

    正确答案:A

  • 第22题：

    对于矩形区域内的常物性，无内热源的导热问题，试分析在下列四种边界条件的组合下，导热物体为铜或钢时，物体中的温度分布是否一样： （1）四边均为给定温度； （2）四边中有一个边绝热，其余三个边均为给定温度； （3）四边中有一个边为给定热流（不等于零），其余三个边中至少有一个边为给定温度； （4）四边中有一个边为第三类边界条件。


    正确答案: （1）一样，因为两种情况下的数学描写中不出现材料物性值；
    （2）一样，理由同上；
    （3）不一样，在给定热流的边上，边界条件中出现固体导热系数；
    （4）不一样，在第三类边界条件的表达式中出现固体导热系数。

  • 第23题：

    单选题
    常物性无内热源一维非稳态导热过程第三类边界条件下可微分得到离散方程，进行计算时要达到收敛需满足（　　）。[2011年真题]
    A

    Bi＜1/2

    B

    Fo≤1

    C

    Fo≤[1/（2Bi＋2）]

    D

    Fo≤1/（2Bi）


    正确答案： B
    解析：
    对非稳态导热的显式格式，其数值解的稳定性要受到稳定性条件的限制。对于第一类边界条件的稳定性（收敛）条件是Fo≤1/2；对于第三类边界条件的稳定性（收敛）条件是Fo≤[1/（2Bi＋2）]。

相关内容