下图中的大正方形ABCD的面积是1平方厘米，其他点都是它所在边的中点。那么，阴影三角形的面积是多少平方厘米？（） A. 5/28 B. 7/34 C. 3/32 D. 5/38

题目
下图中的大正方形ABCD的面积是1平方厘米，其他点都是它所在边的中点。那么，阴影三角形的面积是多少平方厘米？（）


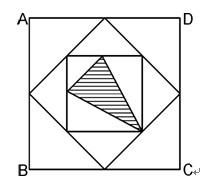
A. 5/28
B. 7/34
C. 3/32
D. 5/38
相似考题

1.：右图中的甲和乙都是正方形，BE=6厘米，EF=4厘米。那么，阴影部分ABC的面积是多少平方厘米？（ ）A．20B．24C．21D．18

2.如图，它是由15个同样大小的正方形组成的。如果这个图形的面积是375平方厘米．那么，它的周长是多少厘米?（ ）

3.右图中的三角形纸板、正方形纸板、圆形纸板的面积都是40cm2，阴影部分的面积总和是30cm2，三张纸板盖住的总面积是70cm2。求三张纸板重叠部分的面积（即A的面积）为多少平方厘米？（）A. 10 B. 15 C. 6 D. 20

4.请教:四川2010年公务员考试《行测》冲刺模考试卷(1)第1大题第12小题如何解答?【题目描述】第12题图中的三角形纸板、正方形纸板、圆形纸板的面积都是40c㎡，阴影部分的面积总和是30c㎡，三张纸板盖住的总面积是70c㎡。求三张纸板重叠部分的面积，即A的面积为多少平方厘米?（　）

参考答案和解析
答案：C
解析：
［解析］ 阴影三角形面积为最小正方形的3/8，最小正方形面积为第二大正方形面积的1/2，第二大正方形面积是最大正方形的1/2，则阴影三角形的面积为3/8×1/2×1/2＝3/32（厘米2）。故选C。
更多“下图中的大正方形ABCD的面积是1平方厘米，其他点都是它所在边的中点。那么，阴影三角形的面积是多少平方厘米？（） ”相关问题

  • 第1题：

    下图中，每个小正方形网格都是边长为1的小正方形，则阴影部分面积最大是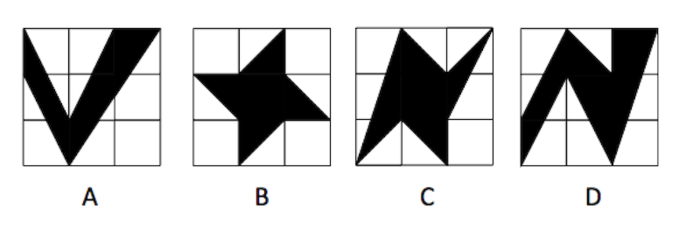： AA
    BB
    CC
    DD


    答案：D
    解析：
    解析:
    根据题目所给图形，可计算得：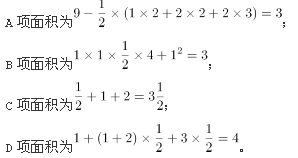

    故正确答案为D。

  • 第2题：

    在下图中，大正方形的边长为10,连接大正方形的各边中点得到小正方形，将小正方 形每边三等分，再将三等分点与正方形的中心和对应的顶点相连，得到如下图形。那么阴影部分面积是（）。



    答案：C
    解析：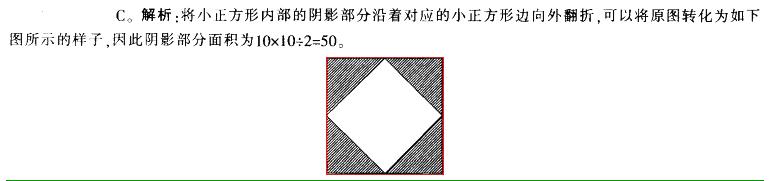

  • 第3题：

    在下图中，大正方形的边长为10，连接大正方形的各边中点得到小正方形，将小正方形 每边三等分，再将三等分点与正方形的中心和对应的顶点相连，得到如下图形。那么阴影部分 面积是（）。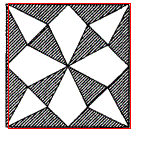


    A.25
    B.100/3
    C.50
    D.75

    答案：C
    解析：
    将小正方形内部的阴影部分沿着对应的小正方形边向外翻折，可以将原图转化为如下 图所示的样子，因此阴影部分面积为10x10+2=50。

  • 第4题：

    如图，AD=DB=DC=10厘米，那么，图中阴影部分的面积是多少平方厘米？（）



    A. 109
    B. 110
    C. 107
    D. 110.25

    答案：C
    解析：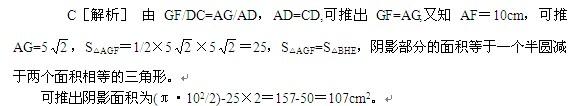

  • 第5题：

    右图中间阴影部分为长方形。它的四周是四个正方形，这四个正方形的周长和是320厘米，面积和是1700，则阴影部分的面积是_____平方厘米。
    A、375 B、400
    C、425 D、430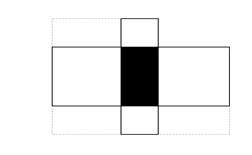

    A. 375
    B. 400
    C. 425
    D. 430

    答案：A
    解析：

  • 第6题：

    正方形ABCD的面积是120平方厘米，E、H分别是AD和DC的中点，求阴影部分的面积（ ）。



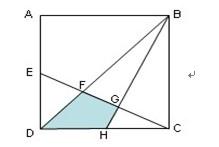    A.14
    B.16
    C.17
    D.18

    答案：A
    解析：

  • 第7题：

    如图所示，ΔABC是直角三角形，四边形和四边形都是正方形，已知4cm，问正方形HFGF的面积是多少？（ ）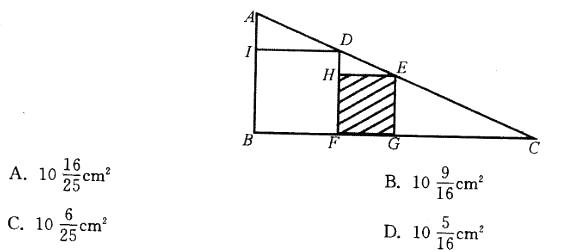


    答案：C
    解析：

  • 第8题：

    如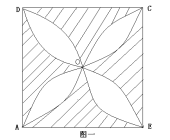，四边形ABCD是边长为1的正方形，弧AOB，BOC，COD，DOA均为半圆，则阴影部分的面积为



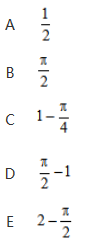    答案：E
    解析：

  • 第9题：

    图中的大正方形ABCD的面积是1平方厘米，其他点都是它所在边的中点。弧是一个内切于小正方形IJKL的半圆弧，PQ、OP是与弧半径相等的圆的四分之一圆弧，则阴影区的面积是多少平方厘米？（ ）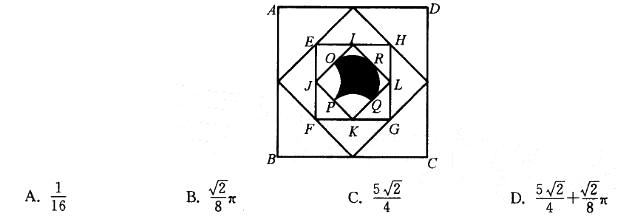


    答案：A
    解析：
    由正方形是大正方形面积的1/4，小正方形IJKL是正方形EFHG面积的1/2，故小正方形IJKL是大正方形ABCD面积的1/8，如下图所示，图中的阴影部分面积是小正方形IJKL 的一半，所以阴影区的面积为大正方形面积的1/16。A为正确选项。

  • 第10题：

    如右上图，正三角形的三个顶点都位于大圆周上，且三条边都与小圆相切。如果正三角形的边长是10厘米，那么图中圆环（阴影部分）的面积是多少平方厘米？ (π=3. 14)( )

    A. 12.56 B. 78.5 C. 314 D. 512.6


    答案：B
    解析：
    连接圆心O与三角形的顶点A及三角形与小圆相切的切点B（见右图）。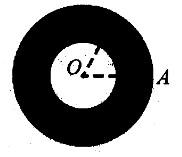

    S圆环 = (OA2-OB2)π= BA2π
    =(10/2)2 π
    =78.5(平方厘米)
    因此，本题正确答案为B。

  • 第11题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )

    A. 11.75 B. 16.45 C. 19.625 D. 39.25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。
    由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10X10X2，所以大半圆的面积是1/2x1/4xπx10x10x2 = 25π(平方厘米)；
    小半圆的面积是1/2πx5x5 = 12. 5π(平方厘米)；
    阴影的面积是25π-12. 5π=12. 5π=39. 25(平方厘米)。
    故本題选D。

  • 第12题：

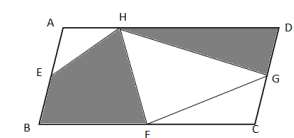
    如图，平行四边形ABCD的面积是54平方厘米，点E、F、G分别是平行四边形ABCD边上的中点，H为AD边上的任意一点，则阴影部分的面积为（ ）平方厘米。


    A. 27
    B. 28
    C. 32
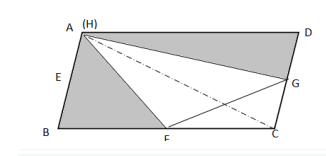
    D. 36

    答案：A
    解析：
    方法一：如图所示，由于H为AD边上的任意一点，假设H点与A点重叠，则左边阴影为三角形ABF，其面积为三角形ABC的一半；右边阴影为三角形ADG，其面积为三角形ACD的一半。因此题目所求为平行四边形ABCD面积的一半，平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。



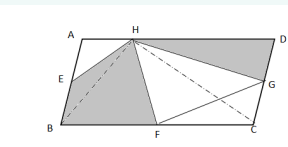
    方法二：如图所示，连接BH和CH，由于点E、F、G分别是平行四边形ABCD边上的中点，则三角形AEH和BEH相等，三角形BFH和CFH相等，三角形CGH和DGH相等，因此题目所求的阴影部分为平行四边形ABCD的一半。平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。

  • 第13题：

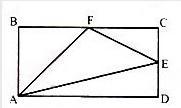
    长方形ABCD的面积是72平方厘米，E、F分别是CD、BC的中点，三角形AEF的面积是（）平方厘米。


    A 24
    B 27
    C 36
    D 40

    答案：B
    解析：
    因为ABF和ADE面积为18,EFC面积为9，用总面积72-18-18-9=27

  • 第14题：

    下图中的甲和乙都是正方形，BE=6厘米，EF=4厘米。那么，阴影部分ABC的面积是多少平方厘米？（ ）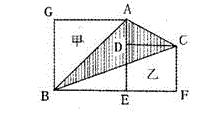


    A. 20
    B. 24
    C. 21
    D. 18

    答案：D
    解析：
    阴影部分ABC的面积等于整个图形面积减去△AGB和△BFC的面积，所以有6×6+4×4+1/2×2×4-1/2×6×6-1/2×10×4 =18平方厘米。故答案为D。

  • 第15题：

    长方形ABCD的面积是72平方厘米，E、F分别是CD，BC的中点。问三角形的面积为多少平方厘米？

    A.24
    B.27
    C.36
    D.40


    答案：B
    解析：

  • 第16题：

    在4×7的方格板纸上面有如阴影所示的“9”字，每个小正方形的面积都是1平方厘米，阴影边缘是线段或圆弧，问纸板中阴影部分的面积是多少平方厘米？（ ）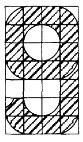


    A. 17
    B. 18
    C. 19
    D. 20

    答案：C
    解析：
    矩形纸板共有28个小正方形，图中非阴影部分比较少，其面积更容易计算。非阴影部分有三个完整的小正方形，经过平移其他部分可以拼成6个小正方形，因此非阴影部分的面积是9平方厘米，即阴影部分的面积是19平方厘米。

  • 第17题：

    如图，有大小两个正方形，其对应边的距离均为1厘米。如果两个正方形之间部分的面积是20平方厘米，那么，小正方形的面积是多少平方厘米？（ ）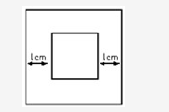


    A4
    B9
    C16
    D25


    答案：C
    解析：
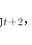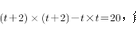    设小正方形的边长为，则大正方形的边长为，依题意有，解之得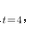，所以面积为16。

    故正确答案为C。

  • 第18题：

    右图中间阴影部分为长方形。它的四周是四个正方形，这四个正方形的周长和是320厘米，面积和是1700，则阴影部分的面积是_____平方厘米。

    A. 375
    B. 400
    C. 425
    D. 430

    答案：A
    解析：
    设小正方形边长x，大正方形边长y，那么阴影部分的面积就是xy。由题意得4x+4x+4y+4y=320，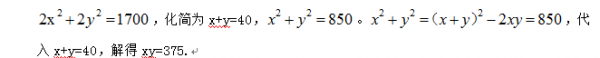

  • 第19题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )
    A. 11.75 B. 16.45 C. 19.625 D. 39. 25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10x10x2，所以大半圆的面积是1/2x1/4xπx10x10x2=25π（平方厘米）；
    小半圆的面积是π/2X5X5 = 12. 5π（平方厘米）；
    阴影的面积是25π-12. 5π=12. 5π=39. 25（平方厘米）。
    故本题选D。

  • 第20题：

    如图，在平行四边形ABCD中，已知三角形ABP、BPC的面积分别是73、100，那么三角形BPD的面积是多少?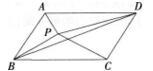

    A.27
    B.36．5
    C.50
    D.无法确定

    答案：A
    解析：

  • 第21题：

    如右图，它是由15个同样大小的正方形组成。如果这个图形的面积是375平方厘米，那么．它的周长是多少厘米?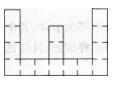

    A.150
    B.155
    C.160
    D.165

    答案：C
    解析：
    每个正方形的面积为375÷15=25平方厘米，边长为5厘米。周长为5×32=160厘米。

  • 第22题：

    已知如图，直角三角形ABC的两直角边AC = 8厘米，BC=6厘米，以AC、BC为边向三角形外分别作正方形ACDE和BCFG，再以AB为边向上作正方形ABMN，其中N点落在DE上，BM交CF于点了，则阴影部分的总面积等于（ ）。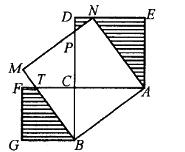

    A. 46平方厘米 B. 38平方厘米
    C. 40平方厘米 D. 48平方厘米


    答案：D
    解析：
    已知ΔABC为直角三角形，AC=8厘米，BC=6厘米，则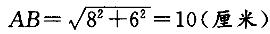。 设四边形ACPN的面积为S1，ΔBCT的面积为S2，四边形CTMP的面积为S3。SACDE + SBGFC = 82 + 62 =102 =SABMN，即S1 + S2 + S阴影=S1 + S2+ S3 + SΔABC ，故S阴影=S3 + SΔABC 。已知四边形ABMN为正方形，则∠BAC + ∠ABC = ∠ABC + ∠CBM，得∠BAC =∠CBM；∠CBM +∠BPM = ∠CBM +∠BTC，则∠BPM =∠BTC。因为AB=BM，所以SΔABT≌SΔBMP（角角边），故S3+SΔBCT=SΔABC +SΔBCT，得S3=SΔABC。故S阴影=2 SΔABC = 2X8X6/2 = 48(平方厘米)。

  • 第23题：

    已知图中三角形ABC的面积为1998平方厘米，是平行四边形DEFC面积的3倍。那么，图中阴影部分的面积是多少平方厘米？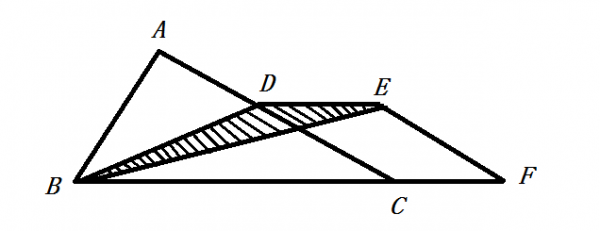


    A. 333
    B. 499
    C. 999
    D. 1333

    答案：A
    解析：
    由图得阴影部分与平行四边形同底等高,所以阴影部分面积是平行四边形的一半，
    因为三角形ABC的面积是1998平方厘米，是平行四边形DEFC的3倍，所以三角形ABC的面积是阴影部分的6倍，则阴影部分面积是8325px2。故选A选项。

相关内容