将2个棱长为30厘米的正方体木块的六面分别全涂成黑色后,都锯成棱长为10厘米的小正方体,问从这些小正方体中随机抽取出多少个,才能保证一定能够在取出的小立方体中挑出8个,拼成外表面全为黑色的,棱长为20厘米的正方体?A. 27 B. 36 C. 40 D. 46
题目
B. 36
C. 40
D. 46
相似考题
更多“将2个棱长为30厘米的正方体木块的六面分别全涂成黑色后,都锯成棱长为10厘米的小正方体,问从这些小正方体中随机抽取出多少个,才能保证一定能够在取出的小立方体中挑出8个,拼成外表面全为黑色的,棱长为20厘米的正方体?”相关问题
-
第1题:
将27个边长为1的小正方体垒成一个大正方体,然后把大正方体全部涂成红色,请问:三面都被涂成红色的小正方体有多少个?()。
A.4
B.6
C.8
D.12
正确答案:C
只有正方体8个顶点处的小正方体三面都被涂成红色。故选C。 -
第2题:
一个正方体木块的体积为1000厘米³,现要把它锯成八块,同样大小的正方体小木块,小木块的棱长是多少?
锯成8块之后,每小块的正方体体积为1000/8=125厘米³
设小木块的棱长是x,则
x³=125,x=5厘米
-
第3题:
9厘米的正方体切成棱长为3厘米的小正方体,可以切成( )个。
A.3
B.9
C.27
D.6
正确答案:C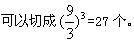
-
第4题:
一块各面均涂有油漆的正方体被锯成1000个同样大小的小正方体,将这些小正方体均匀地搅混在一起,随机地取出一个小正方体,其两面涂有油漆的概率是:A.0.12
B.0.096
C.0.072
D.0.064答案:B解析:1000=10×10×10,即每个边上有10块,两面涂有油漆的只能在边上,共有(10-2)×12=96块,概率为96÷1000=0.096。 -
第5题:
用n个棱长是a cm的小正方体可以摆出“一”字形长方体,如图,n个小正方体拼在一起 时,这个长方体表面积是_______cm2。
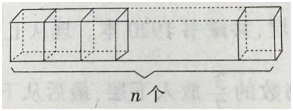 答案:解析:(4n+2)a2。解析:n个小正方体如题干图中所示拼在一起时,组成长为na,宽为a,高为a的长方体,所以表面积为(4n+2)a2 cm2。
答案:解析:(4n+2)a2。解析:n个小正方体如题干图中所示拼在一起时,组成长为na,宽为a,高为a的长方体,所以表面积为(4n+2)a2 cm2。 -
第6题:
有l25个棱长均为1的正方体,其中100个表面为白色,25个表面为蓝色。将这些正方体组成一个大正方体,表面为白色的面积至少为( )。’A.100
B.97
C.94
D.92答案:D解析:题目可转化为表面为蓝色的面积至多为多少,则应把蓝色小正方体尽量放在角和棱上,这样每个小正方体可贡献3个或2个蓝色表面。因此在8个角上用去8个蓝色正方体后,在棱上再放25—8=17个,此时蓝色表面积最大为3×8+17x2=58,表面为白色的面积至少为25×6—58=92.选D。 -
第7题:
如 ,正方体ABCD-A′B′C′D′的棱长为2,F是棱C′D′的中点,则AF的长为
,正方体ABCD-A′B′C′D′的棱长为2,F是棱C′D′的中点,则AF的长为
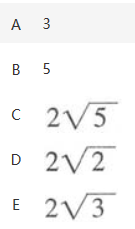 答案:A解析:
答案:A解析:
-
第8题:
有64个棱长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的。现将它们拼成一个4X4X4的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?( )
A. 52 B. 64 C. 72 D. 74答案:D解析:没有露在表面的小正方体有(4一2)3=8(个)是用黑色的。在面上但不在棱上的小正方体有(4-2)2X6 = 24(个),其中30-8 = 22(个)用黑色的。这样,在表面积为4X4X6 = 96(平方厘米)的小正方形中,22个是黑色,共22平方厘米,有96-22 = 74(平方厘米)是白色,在大正方体的表面上白色部分最多可以是74平方厘米。因此,本题正确答案为D。 -
第9题:
边长为4的正方体木块,各面均涂成红色,将其锯成64个边长为1的小正方体,并将它们搅匀混在一起,随机取出一个小正方体,恰有两面为红色的概率是( )。 答案:A解析:本题主要考查概率的计算及空间想象能力。根据题意,是将大正方体分成四层,每层16个小正方体,两个面都为红色的处于上(除过顶点处),每条棱有2个,12条棱共有24个符合条件的小正方体,因此取到面为红色的小正方体的概率为
答案:A解析:本题主要考查概率的计算及空间想象能力。根据题意,是将大正方体分成四层,每层16个小正方体,两个面都为红色的处于上(除过顶点处),每条棱有2个,12条棱共有24个符合条件的小正方体,因此取到面为红色的小正方体的概率为
-
第10题:
如图,A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )。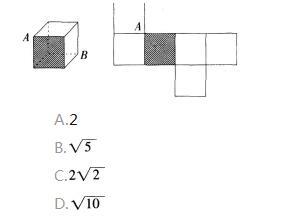 答案:B解析:
答案:B解析:
-
第11题:
如图所示,有一只蚂蚁在正方体某条棱的A处,它想尽快地游览完正方体的各个面,然后回到A处,如果正方体的棱长为10cm,则这只蚂蚁通过的最短路程为( )。
A. 55cm
B. 30 cm
C. 120cm
D. 42 cm
正确答案:B
80.【答案】B。解析:将正方体展开计算两点直线距离。 -
第12题:
如图1,正方体ABCDA′B′C′D′中,EE′∥FF′∥BB′,平面AEE′A′与平面ABB′A′成15°角,平面AFF′A′与平面ADD′A′成30°角.如果正方体的棱长为1,那么几何体AEF A′E′F′的体积等于____.
参考答案3-√3 -
第13题:
把棱长为4的正方体分割成24个棱长为整数的正方体(且没有剩余),其中棱长为1的正方体的个数为( )
A、 12
B、 15
C、 18
D、 21
正确答案:D
-
第14题:
在棱长为1的正方体上切下两个角,所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体,六面体体积为原正方体体积的1/24,则六面体表面积为原正方体表面积的:A.1/4
B.1/6
C.1/8
D.1/10答案:C解析:由题意知切下的角是底面为正三角形、侧面为三个等腰直角三角形的三棱锥,设切下角的直角边为x,则六面体体积=2×三棱锥体积=2×(1/3)×(x2/2)×x=1/24,解得x=1/2。所以六面体每个面是直角边为1/2的等腰直角三角形,六面体的每个面相当于边长为1的正方形面积的1,所以六面体的表面积为原正方体的1/8。故本题选C。 -
第15题:
一个木制正方体在表面涂上颜色,将它的每条棱三等分,然后从等分点将正方体展开,得到27个小正方体,将这些小正方体充分混合后,装入一个口袋,从这个口袋中随机取出两个小正方体,其中一个正方体只有一个面涂有颜色,另一个只有2个面涂有颜色的概率约为( )A. 0.05
B. 0.17
C. 0.34
D. 0.67答案:C解析:涂一面的6个 涂2面的12个 满足条件情况72个,经计算为0.34 -
第16题:
一个棱长为6厘米的正方体木块,表面涂上红色,然后把它锯成边长为1厘米的小正方体,设一面红色的有a块,两面红色的有b块,三面红色的有c块,没有红色的有d块,则a,b,c,d的最大公约数为( )A.2
B.4
C.6
D.8
E.12答案:D解析:
-
第17题:
将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料,然后将其切成64个棱长1厘米的小正方体,再用这些小正方体堆成棱长4厘米的大正方体,且使黑色的面向外露的面积要尽量大,问大正方体的表面上有多少平方厘米是黑色的?A. 88
B. 84
C. 96
D. 92答案:A解析:白色长方体可以看做64个小正方体平铺,由4个角,24个棱和36个中间小正方体构成,角上的4个小正方体有4个面被刷成了黑色,棱上的24个小正方体连续的3个面被刷成了黑色,中间的36个小正方体相对的2个面被刷成了黑色;拼成的大正方体有8个角,24个棱和24个单面,拼接时有4个角需用之前棱上的小正方体替换,每替换一次缺一个黑色面,角上共缺了4个;由于4个棱上的正方体替换到了角上,此时棱上又少了4个小正方体,需用对面为黑色的小正方体替换,每替换一次缺一个黑色面,棱上共缺了4个。大正方体的表面积为4×4×6=96平方厘米,大正方体的表面上共有96-4-4=88平方厘米是黑色的。因此,本题选A。 -
第18题:
边长为4的正方体木块,各面均涂成红色,将其锯成64个边长为1的小正方体,并将它们搅匀混在一起,随机抽取一个小正方体,恰有两面为红色的概率是( )
 答案:A解析:锯成64个边长为1的小正方体后,涂色的面有以下几种情况:涂3面的小正方体分别在大正方体的8个顶点处,共有8个;涂2面的小正方体分别是大正方体的每条棱的中间的2个,而大正方体共有12条棱,那么,涂2面的小正方体有2×12=24个;涂1面的小正方体分别是每个面的中间的4个,而大正方体共有6个面,那么,涂1面的小正方体有4×6=24个;6个面都没有涂色的小正方体有64-8-24-24=8个,则随机抽取一个小正方体,恰有两面为红色的概率是
答案:A解析:锯成64个边长为1的小正方体后,涂色的面有以下几种情况:涂3面的小正方体分别在大正方体的8个顶点处,共有8个;涂2面的小正方体分别是大正方体的每条棱的中间的2个,而大正方体共有12条棱,那么,涂2面的小正方体有2×12=24个;涂1面的小正方体分别是每个面的中间的4个,而大正方体共有6个面,那么,涂1面的小正方体有4×6=24个;6个面都没有涂色的小正方体有64-8-24-24=8个,则随机抽取一个小正方体,恰有两面为红色的概率是

-
第19题:
把棱长为4的正方体分割成24个棱长为整数的正方体(且没有剩余),其中棱长为1的正 方体的个数为()。
A. 12 B. 15 C. 18 D. 21答案:D解析:设分割后棱长为1、2、3 .的正方体分别有x,y,z个,则有
