平行四边形ABCD如右图所示,E为AB上的一点,F、G分别是AC和DE、DB的交点。若AB=3AE,则四边形BEFG与ABCD的面积之比是: A.2︰7 B.3︰13 C.4︰19 D.5︰24
题目
B.3︰13
C.4︰19
D.5︰24
相似考题
更多“平行四边形ABCD如右图所示,E为AB上的一点,F、G分别是AC和DE、DB的交点。若AB=3AE,则四边形BEFG与ABCD的面积之比是: ”相关问题
-
第1题:
有关系模式R=ABCD,其函数依赖集为F={A→B,B→C,AB→D,AB→E,A→DE},则F的最小覆盖( )。
A.G1={A→B,A→C,A→D,A→E)
B.G2={A→B,B→C,AB→D}
C.G3=={A→B,B→C,A→D,A→E}
D.G4={A→C,A→D,A→E}
正确答案:C
-
第2题:
平行四边形中,已知AB、BC及其夹角∠ B(∠ B是锐角),能求出平行四边形ABCD的面积S吗?如果能,写出用AB,BC及其夹角∠ B表示S的式子。
S=BC×AB×sinB
-
第3题:
设关系模式R (U,F),其中U为属性集, F是U上的一组函数依赖,那么函数依赖的公理系统(Armstrong公理系统)中的合并规则是指为( )为F所蕴涵。
A.若A→B,B→C,则A→CB.若Y⊆X⊆U,则X→Y。C.若A→B,A→C ,则A→BCD.若A→B,C⊆B,则A→C
正确答案:C
-
第4题:
如下图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.
 答案:解析:证明:如右图所示,∵四边形ABCD为平行四边形,∴BO=DO,
答案:解析:证明:如右图所示,∵四边形ABCD为平行四边形,∴BO=DO,
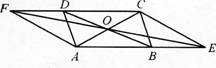
又∵AB∥CD,∴∠FDO=∠EB0

-
第5题:
如图,D是△ABC内的一点,BD⊥CD,AD=6,BD=8,CD=6,E,F,G,H分别是AB,AC,CD, BD的中点.则四边形EFGH的周长是()。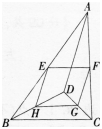 A.12
A.12
B.14
C.15
D.16答案:D解析:因为BD⊥CD,BD=8,CD=6,由勾股定理可知BC=10。由三角形中位线定理可知EH=FG=
-
第6题:
如右图,在梯形ABCD中,点E、F分别是腰AB、CD上的点.
(1)证明:如果E、F为中点时,有 EF=1/2(AD+BC);
(2)请写出(1)中命题的逆命题,并判断该逆命题是否成立,若成立,请给予证明;若不成立,请说明理由.
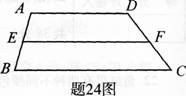 答案:解析:(1)证明:连接AC,设AC中点为日,连接EH、FH
答案:解析:(1)证明:连接AC,设AC中点为日,连接EH、FH

逆命题不成立.
理由如下:连接AC,连接BD,延长AD至M使DM=AD,延长BC至N,使CN=AD,连接MN、DN.由DM平行且等于CN可知,DN平行且等于AC由ADBN可知,BD+DM>BN,即BD+AC>BC+AD
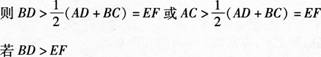
又AD<EF可知AD<EF<BD过点D作直线交AB于Q,则AD<DQ<BD,其中必有DQ=EF同理,若AC>EF,Q为DC上-点,则必有AQ=EF且A、D均不是AB、CD的中点故命题错误. -
第7题:
如右图,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周长为( ).
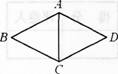 A.20
A.20
B.18
C.16
D.15答案:C解析:由“菱形的每一条对角线平分-组对角”知,在△ABC中,∠BAC=60。,又由“菱形的四条边相等”知,△ABC为正三角形,得AB=4.故菱形的周长为16. -
第8题:
如右图所示,△ABC是等腰直角三角形,AB=12,AD的长度是CD的2倍,四边形EBCD与△AED的面积之比为3:2,问AE的长度是多少( )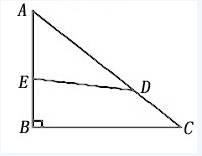
A.6.9 B.7.1 C.7.2 D.7.4答案:C解析:C。由题意可知三角形AED和三角形ABC的面积比为2︰5,AD/AC=2/3,得(0.5AE×AD)/(0.5AB×AC)=2/5,解得AE=7.2。 -
第9题:
如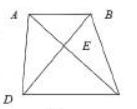 ,在四边形ABCD中,AB//CD,AB与CD的边长分别为4和8,若ABE的面积为4,则四边形ABCD的面积为( )A.24
,在四边形ABCD中,AB//CD,AB与CD的边长分别为4和8,若ABE的面积为4,则四边形ABCD的面积为( )A.24
B.30
C.32
D.36
E.40答案:D解析: -
第10题:
如右图所示,梯形ABCD的对角线AC丄BD,其中AD=1/2,BC=3,AC=2,BD=2.1,则梯形ABCD的髙AE的值是()。
 答案:C解析:由ACXBD=(AD+BC)XAE=>AE=42/45。
答案:C解析:由ACXBD=(AD+BC)XAE=>AE=42/45。 -
第11题:
如图,平行四边形ABCD,∠ADC的角平分线DE交BC于E,且AD=14,DC=9,
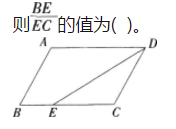
 答案:C解析:
答案:C解析:
-
第12题:
已知圆内接四边形ABCD中,AB、CD的延长线交与点F,则F=()
- A、40°
- B、50°
- C、60°
- D、70°
正确答案:A -
第13题:
有关系模式R=ABCD,其函数依赖集为F=A->B,B->C,AB->D,AB->E,A->DE,则F的最小覆盖为______。
A.G1=A->B,A->C,A->D,A->E
B.G2=A->B,B->C,AB->D
C.G3=A->B,B->C,A->D,A->E
D.G4=A->C,A->D,A->E
正确答案:C
-
第14题:
对边相等,对角相等的凸四边形,是平行四边形吧?方法①∠B小于90°;
左上为A,左下为B,右下为C,右上为D;
已知∠B=∠D;AB=CD;
证明:过A作AN⊥BC于N;
过C作CM⊥AD于M;
连接AC
∵AN⊥BC;CM⊥AD
∴∠ANB=∠DMC=90°
又∵∠B=∠D;AB=CD
∴△ANB=△DMC(AAS)
∴AN=CM;BN=DM
又∵∠ANB=∠DMC=90°,AC=AC
∴△ACD=△AMD(HL)
∴AM=DN
又∵BN=DM
∴BD=AC
∵BD=AC;AB=CD
∴凸四边形ABCD为平行四边型。
方法②∠B大于90°
左上为A,左下为B,右下为C,右上为D;
已知∠B=∠D;AB=CD;
证明:延长CD,过A作AN⊥BC于N;
延长AB,过C作CM⊥AD于M;
连接AC
∵AN⊥BC;CM⊥AD
∴∠ANB=∠DMC=90°
又∵∠B=∠D;AB=CD
∴△ANB=△DMC(AAS)
∴AN=CM;BN=DM
又∵∠ANB=∠DMC=90°,AC=AC
∴△ACD=△AMD(HL)
∴AM=DN
又∵BN=DM
∴BD=AC
∵BD=AC;AB=CD
∴凸四边形ABCD为平行四边型。
方法③∠B等于90°
证明:∵∠B=∠D=90°;AB=CD;AC=AC
∴△ABC=△ADC(HL)
∴AB=CB
∵BD=AC;AB=CD
∴凸四边形ABCD为平行四边型。
有错吗?若我的证明有错请明示,我知道有个反例,但它是凹四边形。
是平行四边形 -
第15题:
如图:已知圆0,点P在圆外,D,E在圆上,PE交圆于C,PD与圆相切,G为CE上一点且满足PG=PD,连接DG并延长交圆于A,作弦AB⊥EP,垂足为F。
(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。答案:解析:(1)证明:∵PG=PD,∴∠PGD=∠PDG,又∵∠AGF=∠PGD,∠PDG=∠ABD,∴∠AGF=∠ABD,∴∠ADB=∠AFP=90°,∴AB为圆的直径。
-
第16题:
在平行四边形ABCD中,∠DAB=60,AB=15cm,已知圆O的半径等于3cm,AB,AD分别与圆O相切于点E,F.圆0在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止.试求圆O滚过的路程.答案:解析:
-
第17题:
如右图,在直角梯形ABCD中,AB,∥CD,AD⊥CD,AB=1cm,AD=6cm,CD=9cm,则BC=________cm.
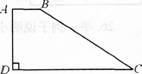 答案:解析:
答案:解析:
-
第18题:
如图,平面四边形ABCD中,AB=2,BC=4,CD=5,DA=3,
(1)若∠B与∠D互补,求AC2的值;
(2)求平面四边形ABCD面积的最大值。 答案:解析:
答案:解析: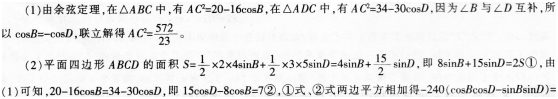
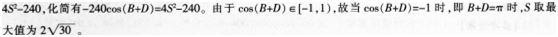
-
第19题:
如右图所示,梯形ABCD的对角线AC⊥BD,其中AD=1/2,BC=3,AC=14/5 ,BD=2.1.问梯形ABCD的高AE的值是: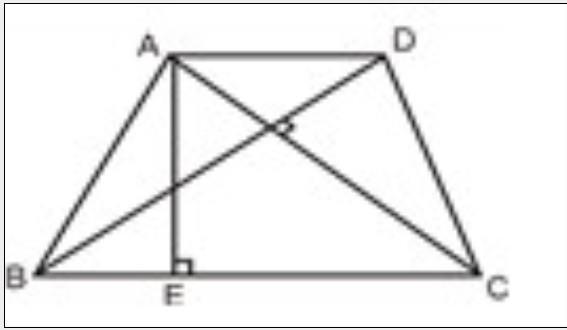
A. 43/24
B. 1.72
C. 42/25
D. 1.81答案:C解析:解题指导: C。 -
第20题:
如图,在梯形ABCD中,AB//CD,O为AC与BD的交点,CO=2AO,则梯形ABCD与三角形AOB的面积之比为: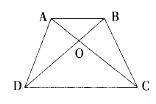 A.6:1
A.6:1
B.7:1
C.8:1
D.9:1答案:D解析:在梯形中,上底与下底平行,可得△AOB~△COD,其面积之比等于对应边AO、CO之比的平方,为1:4。△AOB与△BOC可看成两个等高的三角形,面积之比等于底AO、CO之比,为1:2。显然△AOD与△BOC面积相等。设△AOB面积为1,则梯形面积为1+2+2+4=9。故所求为9:1。 -
第21题:
如右图所示,在△ABC:中,D为AC的中点,E在BC上,且 BE : EC=1 : 2,AE与BD交于F。则△BEF与四边形EFDC 的面积之比为( )。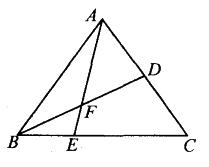
A. 1 : 3 B. 1 : 4
C. 1 : 5 D. 1 : 6答案:C解析: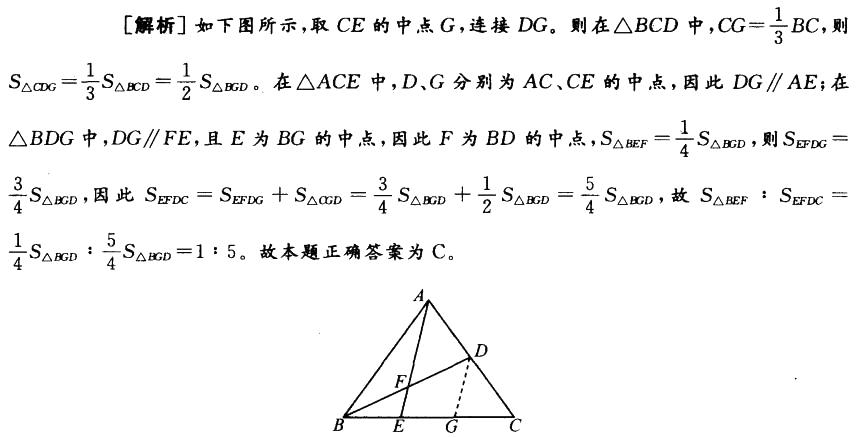
-
第22题:
如图,平行四边形ABCD的面积是54平方厘米,点E、F、G分别是平行四边形ABCD边上的中点,H为AD边上的任意一点,则阴影部分的面积为( )平方厘米。
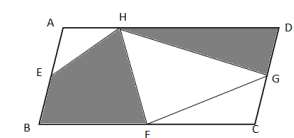 A. 27
A. 27
B. 28
C. 32
D. 36答案:A解析:方法一:如图所示,由于H为AD边上的任意一点,假设H点与A点重叠,则左边阴影为三角形ABF,其面积为三角形ABC的一半;右边阴影为三角形ADG,其面积为三角形ACD的一半。因此题目所求为平行四边形ABCD面积的一半,平行四边形ABCD的面积是54平方厘米,则阴影部分面积为27平方厘米。因此,本题答案为A选项。
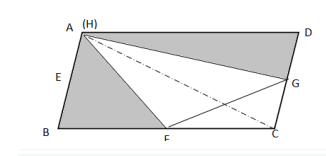
方法二:如图所示,连接BH和CH,由于点E、F、G分别是平行四边形ABCD边上的中点,则三角形AEH和BEH相等,三角形BFH和CFH相等,三角形CGH和DGH相等,因此题目所求的阴影部分为平行四边形ABCD的一半。平行四边形ABCD的面积是54平方厘米,则阴影部分面积为27平方厘米。因此,本题答案为A选项。
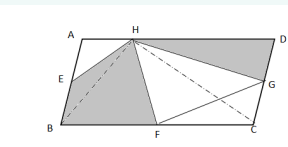
-
第23题:
逻辑代数式子f=AB+ABC+AB(C+D),则f的简化式子为()。
- A、AB
- B、A+B
- C、ABC
- D、ABCD
正确答案:A
