在平行四边形ABCD中,∠DAB=60°,AB=15cm.已知⊙O的半径等于3cm,AB,AD分别与⊙O相切于点E,F,⊙O在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止,试求⊙O滚过的路程.
题目
在平行四边形ABCD中,∠DAB=60°,AB=15cm.已知⊙O的半径等于3cm,AB,AD分别与⊙O相切于点E,F,⊙O在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止,试求⊙O滚过的路程.
相似考题
更多“在平行四边形ABCD中,∠DAB=60°,AB=15cm.已知⊙O的半径等于3cm,AB,AD分别与⊙O相切于点E,F,⊙O在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止,试求⊙O滚过的路程.”相关问题
-
第1题:
如图。在直角梯形ABCD中,AB∥CD,∠BAD=90o,且AB=8,AD=3,CD=4,动点P,Q分别以点B和点A为起点同时出发,点P沿B→A,以每秒1个单位速度运动,终点为点A;点Q沿A→D→C→B,以每秒1.5个单位速度运动,终点为点B。设△APQ的面积为y,运动时间为x。
(1)求y关于x的函数解析式y=f(x);
(2)画出函数y=f(x)的图象。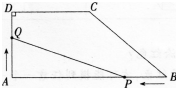 答案:解析:
答案:解析:
(2)函数图象如图所示: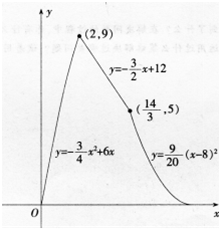
-
第2题:
如下图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.
 答案:解析:证明:如右图所示,∵四边形ABCD为平行四边形,∴BO=DO,
答案:解析:证明:如右图所示,∵四边形ABCD为平行四边形,∴BO=DO,
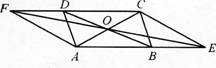
又∵AB∥CD,∴∠FDO=∠EB0

-
第3题:
如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.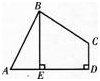
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.答案:解析: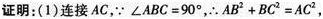
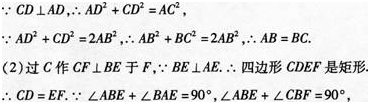

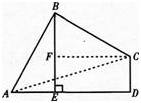
-
第4题:
如图⊙O和⊙O’相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交⊙O于点E.证明: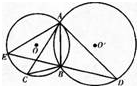
(1)AC?BD=AD?AB;
(2)AC=AE.答案:解析: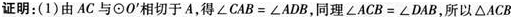

-
第5题:
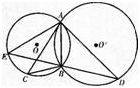
如图所示,梯形ABCD的两条对角线AD、BC相交于O,EF平行于两条边且过O点。现已知AB=6,CD=18。问EF的长度为多少?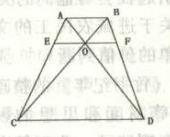 A. 8.5
A. 8.5
B. 9
C. 9.5
D. 10答案:B解析:解题指导: 18*BF/BD=6*DF/BD, BF/DF=1:3, OF/CD=1:4, OE/CD=1:4, EF=CD/2=9,故答案为B。 -
第6题:
平行四边形ABCD如右图所示,E为AB上的一点,F、G分别是AC和DE、DB的交点。若AB=3AE,则四边形BEFG与ABCD的面积之比是: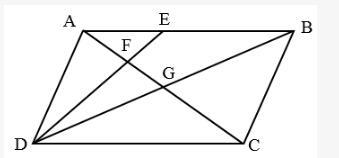 A.2︰7
A.2︰7
B.3︰13
C.4︰19
D.5︰24答案:D解析:第一步,本题考查几何问题,属于平面几何类,用赋值法解题。
第二步,题干没给出具体数值,可以采用赋值法解题。赋值AB=3,平行四边形ABCD的高为4,则AE=1;由于△AEF相似于△CDF,则两个三角形的高之比为AE:DC=1︰3,可知△AEF的高为4×1/4=1。△ABG与△CDG全等,则△ABG的高为4÷2=2。
第三步,四边形BEFG面积=△ABG面积-△AEF面积=
四边形ABCD面积=3×4=12,两者之比为5/2 ︰12=5︰24。
因此,选择D选项。 -
第7题:
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8, AB∥DE,求△DEC的周长。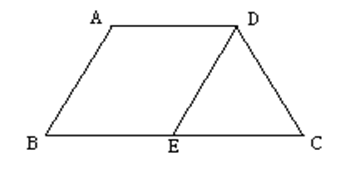 答案:解析:15
答案:解析:15 -
第8题:
在A、B、O血型反定型中,A红细胞(-),B红细胞(+),O红细胞(-),此血型结果为:( )A.A
B.B
C.O
D.AB答案:A解析: -
第9题:
分别用分析法,综合法证明如下命题。
命题:如图。三角形ABC的角B和角C的角平分线相交于点O,过点O作平行于底边BC的直线,交AB边于点D,交AC边于点E,则DE=BD+EC。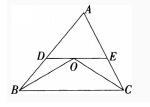 答案:解析:
答案:解析:
-
第10题:
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。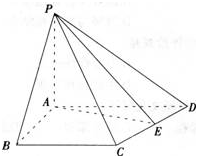 答案:解析:
答案:解析:
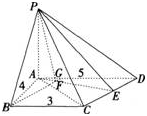
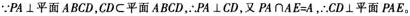

-
第11题:
某医院同日生下四个孩子,其血型分别是O、A、B和AB,这四孩子的双亲的血型是O与O;AB与O;A与B;B与B。请判断这四个孩子的父母的血型。
正确答案: O血型的孩子,其父母可能是O与O;
A血型的孩子其可能父母是AB与O;
B血型的孩子其父母可能是B和B;
AB型的孩子其可能父母是A和B。 -
第12题:
多选题不会产生O血型子女的夫妇是()。AAB与AB夫妻
BAB与O夫妻
CAB与A夫妻
DAB与B夫妻
正确答案: A,B解析: 暂无解析 -
第13题:
如图:已知圆0,点P在圆外,D,E在圆上,PE交圆于C,PD与圆相切,G为CE上一点且满足PG=PD,连接DG并延长交圆于A,作弦AB⊥EP,垂足为F。
(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。答案:解析:(1)证明:∵PG=PD,∴∠PGD=∠PDG,又∵∠AGF=∠PGD,∠PDG=∠ABD,∴∠AGF=∠ABD,∴∠ADB=∠AFP=90°,∴AB为圆的直径。
-
第14题:
在平行四边形ABCD中,∠DAB=60,AB=15cm,已知圆O的半径等于3cm,AB,AD分别与圆O相切于点E,F.圆0在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止.试求圆O滚过的路程.答案:解析:
-
第15题:
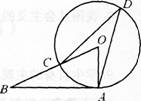
如右图,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙0上,且∠OBA=40°,则∠ADC=_______.
 答案:解析:
答案:解析: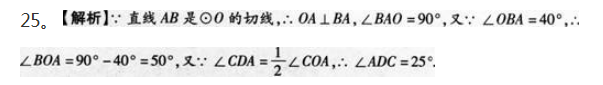
-
第16题:
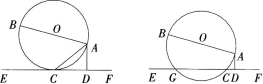
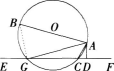
如图,AB是⊙O的直径,AC是弦,直线EF和⊙O相切与点C,AD⊥EF,垂足为D。
(1)若 ∠DAC=63°,求∠BAC;(5分)
(2)若把直线EF向上平行移动,如图,直线EF交 ⊙O于G和C两点,若题中的其他条件不变,这时与∠DAC相等的角是哪一个 为什么 (5分)
 答案:解析:(1)证明:连接OC,则OC⊥EF,且OC=OA,易得∠OCA=∠OAC。 ∵AD⊥EF,∴OC∥AD。∴∠OCA=∠CAD,∴∠CAD=∠OAC=63°
答案:解析:(1)证明:连接OC,则OC⊥EF,且OC=OA,易得∠OCA=∠OAC。 ∵AD⊥EF,∴OC∥AD。∴∠OCA=∠CAD,∴∠CAD=∠OAC=63°
(2)与∠CAD相等的角是∠BAG。
证明如下:如图,连接BG。∵四边形ACGB是⊙O的内接四边形.
∴∠ABG+∠ACG=180°。
∵D,C,G共线,∴∠ACD+∠ACG=180°。
∴∠ACD=∠ABG。
∵AB是⊙O的直径,∴∠BAG+∠ABG=90°
∵AD⊥EF∴∠CAD+∠ACD=90°∴∠CAD=∠BAG
-
第17题:
如图,在梯形ABCD中,AB//CD,O为AC与BD的交点,CO=2AO,则梯形ABCD与三角形AOB的面积之比为: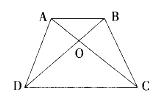 A.6:1
A.6:1
B.7:1
C.8:1
D.9:1答案:D解析:在梯形中,上底与下底平行,可得△AOB~△COD,其面积之比等于对应边AO、CO之比的平方,为1:4。△AOB与△BOC可看成两个等高的三角形,面积之比等于底AO、CO之比,为1:2。显然△AOD与△BOC面积相等。设△AOB面积为1,则梯形面积为1+2+2+4=9。故所求为9:1。 -
第18题:
细直杆AB由另二细杆O1A与O2B铰接悬挂。O1ABO2并组成平等四边形。杆AB的运动形式为: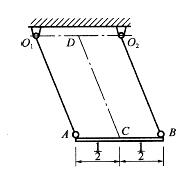 A.平移(或称平动)
A.平移(或称平动)
B.绕点O1的定轴转动
C.绕点D的定轴转动(O1D)=DO2=BC=l/2,AB=l
D.圆周运动答案:A解析:提示 根据平移刚体的定义。 -
第19题:
椭圆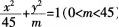 的焦点分别是F1和F2,已知椭圆的离心率
的焦点分别是F1和F2,已知椭圆的离心率
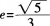 .过中心O
.过中心O
作直线与椭圆交于A,B两点,O为原点,若△ABF2的面积是20。
(1)求m的值;
(2)直线AB的方程。答案:解析:(1)
(2)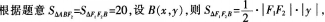
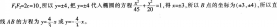
-
第20题:
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。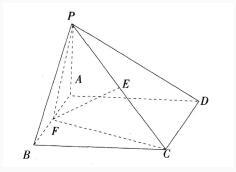 答案:解析:
答案:解析:
-
第21题:
已知四棱锥P-ABCD底面为直角梯形,AB平行于DC,∠DAB=90°,PA垂直于底面ABCD,PA=AD=DC=

AB=1,M为PB中点。
(1)求证:面PAD⊥面PCD;
(2)求面AMC与面BMC所成二面角的余弦值。答案:解析:(1)∵PA⊥面ABCD,CD⊥AD, ∴由三垂线定理,得CD⊥PD。
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD。
又CD面PCD,∴面PAD⊥面PCD。
(2)作AN⊥CM,垂足为N,连结BN。
在Rt△PAB中,∵M是斜边PB中点,
∴AM=MB.

-
第22题:
不会产生O血型子女的夫妇是()。
- A、AB与AB夫妻
- B、AB与O夫妻
- C、AB与A夫妻
- D、AB与B夫妻
正确答案:A,B,C,D -
第23题:
在铰链四杆机构ABCD中,已知AB=25mm,BC=70mm,CD=65mm,AD=95mm,当AD为机架时,是()机构;当AB为机架时,是()机构。
正确答案:曲柄摇杆机构;双曲柄机构
