已知一个箱子中装有12件产品，其中有2件次品。若从箱子中随机抽取2件产品进行检验，则恰好抽到1件次品的概率是：

题目
已知一个箱子中装有12件产品，其中有2件次品。若从箱子中随机抽取2件产品进行检验，则恰好抽到1件次品的概率是：

相似考题

1.一箱产品中有a件正品和b件次品,若随机地将产品一个接一个的摸取出来,(1)不放回抽取;(2)有放回抽取。求第k次摸到的是正品的概率。

2.设有某产品一盒共10只，已知其中有3只次品。从盒中任取两次，每次任取1只，作不放回抽样，则连续两次抽到次品的概率为( )。A．1/15B．1/12C．2/9D．3/10

3.甲箱中有5个正品，3个次品；乙箱中有4个正品，3个次品。从甲箱中任取3个产品放入乙箱，然后从乙箱中任取1个产品，则这个产品是正品的概率为( )。A．0.176B．0.2679C．0.3342D．0.5875

4.一批产品20个,其中有5个次品,从这批产品中随意抽取4个,求(1)这4个中的次品数X的分布列;(2)p(X

更多“已知一个箱子中装有12件产品，其中有2件次品。若从箱子中随机抽取2件产品进行检验，则恰好抽到1件次品的概率是： ”相关问题

  • 第1题：

    某轴承厂有甲、乙、丙三个车间，各车间生产的轴承数量分别占全厂的40%、30%、 30%，各车间的次品率分别为3%、4%、5%(正品率分别为97%、96%、95%)。以上叙述如下图所示。

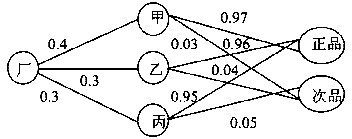
    在图中，从“厂”结点出发选择三个车间产品的概率分别为0.4、0.3、0.3，从各“车间”结点出发选择“正品”或“次品”的概率如图所示。从“厂”结点出发，到达“正品”(或“次品”)结点，可以有多条路径。例如，路径“厂—甲一次品”表示该厂甲车间生产的次品，其概率P(厂一甲一次品)应等于各段上的概率之积。而该厂总的次品率应等于从“厂”结点到达“次品”结点的所有路径算出的概率之和(全概率公式)。而其中每条路径算出的概率在总概率中所占的比例，就是已知抽取产品结果再推测其来源(路径)的概率(逆概率公式)。根据以上描述，可以算出，该厂的正品率约为(53)。如果上级抽查取出了一个次品，那么该次品属于甲车间生产的概率约为(54)。

    A．0.963

    B．0.961

    C．0.959

    D．0.957


    正确答案：B

  • 第2题：

    (本题满分10分) 设20件产品中有3件次品，从中任取两件，在已知其中有一件是次品的条件下，求另一件也是次品的概率．


    正确答案：

  • 第3题：

    有7件产品，其中有3件是次品。每次抽查一件产品(不放回)，能够恰好在第四次找出3件次品的概率为（ ）。

    A．9/56

    B．3/35

    C．3/28

    D．1/7


    正确答案：B

  • 第4题：

    已知甲、乙两箱中装有同种产品，其中甲箱中装有3件合格品和3件次品，乙箱中仅装有3件合格品．从甲箱中任取3件产品放入乙箱后，乙箱中次品件数的数学期望和从乙箱中任取一件产品是次品的概率分别为（　　）

    A．2/3，1/4
    B．2/5，1/4
    C．2/3，1/3
    D．1/3，1/4

    答案：A
    解析：
    乙箱中可能的次品件数为0，1，2，3，分别求出其概率，再按定义求数学期望即可；而求从乙箱中任取一件产品是次品的概率，涉及到两次试验，是典型的用全概率公式的情形，第一次试验的各种可能结果（取到的次品数）就是要找的完备事件组．
    ①X的可能取值为0，1，2，3，X的概率分布为

  • 第5题：

    从一批有10件正品及2件次品的产品中，不放回地一件一件地抽取产品，设每个产品被抽到的可能性相同，求直到取出正品为止所需抽取的次数X的概率分布。


    答案：
    解析：
    由题意，x的所有可能的取值为1，2，3，

  • 第6题：

    设50件产品中，45件是正品，5件是次品，从中任取3件，求其中至少有l件
    是次品的概率(精确到0．01)．


    答案：
    解析：

  • 第7题：

    10件产品中4件为次品,6件为正品,现抽取2件产品.
    　　(1)求第一件为正品,第二件为次品的概率；
    　　(2)在第一件为正品的情况下,求第二件为次品的概率；
    　　(3)逐个抽取,求第二件为正品的概率.


    答案：
    解析：
    (1)令Ai={第i次取到正品}（i=1，2），则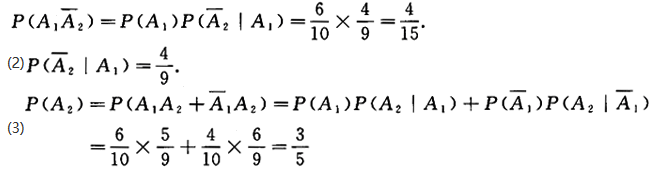

  • 第8题：

    一批产品有10个正品2个次品,任意抽取两次,每次取一个,抽取后不放回,求第二次抽取次品的概率.


    答案：
    解析：
    【解】令A1={第一次抽取正品}，A2={第一次抽取次品}，B={第二次抽取次品}，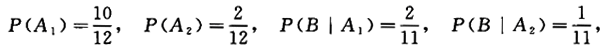

    由全概率公式得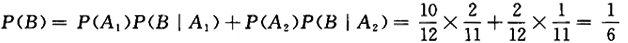

    注解 不放回抽取的情况下，第一次抽取的结果未知时，第二次抽取某种产品的概率与第一次抽取的概率相同。

  • 第9题：

    已知一批产品的次品率为4%，从中有放回地抽取5个，则5个产品中没有次品的概率为（）

    • A、0.815
    • B、0.17
    • C、0.014
    • D、0.999

    正确答案:A

  • 第10题：

    设工厂A和工厂B的产品的次品率分别为1%和2%，现从由A和B的产品分别占60%和40%的一批产品中随机抽取一件，发现是次品，则该次品属于A生产的概率是（）.


    正确答案:3/7

  • 第11题：

    设工厂A和工厂B的产品的次品率分别是1%和2%，现在从由A和B的产品分别是60%和40%的产品中随机抽取一件，发现是次品，则该次品属于A生产的概率是（）

    • A、2/7
    • B、3/7
    • C、2/9
    • D、1/5

    正确答案:B

  • 第12题：

    单选题
    已知一批产品的次品率为4%，从中有放回地抽取5个，则5个产品中没有次品的概率为（）
    A

    0.815

    B

    0.17

    C

    0.014

    D

    0.999


    正确答案： A
    解析： 暂无解析

  • 第13题：

    桌子上有10个杯子，其中有2个次品，现从中随机抽取3件，则其中至少有一个次品的概率为( )。

    A．0.47

    B．0.53

    C．0.67

    D．0.93


    正确答案：B
    解析：10个杯子随机抽取3个，共有个样本点；其中3个中有一个次品的样本点数为3个中有2个次品的样本点数为所以“3个中至少有1个次品”的样本点数为，则所求的概率为：

  • 第14题：

    一批产品共50件,其中46件合格品,4件次品,从中任取3件,其中有次品的概率是多少? 次品不超过2件的概率是多少?


    参考答案：

  • 第15题：

    在一批N个产品中有M个次品，从这批产品中任取n个产品，其中含有m个次品的概率是( )。



    答案：B
    解析：
    这是个古典概率问题

  • 第16题：

    有10件产品，其中8件是正品，2件是次品．甲、乙两人先后各抽取1件产品，
    求甲先抽到正品的条件下，乙抽到正品的概率．


    答案：
    解析：
    这是求在甲事件发生的条件下，乙事件发生的概率，故是条件概率．设A={甲抽到正品}，B={乙抽到正品}，所求为P(B|A)．
    解法l在缩小的样本空间中求条件概率，此时样本空间的样本点为9件产品中有7件正品，2件次品，所以


  • 第17题：

    从含有98件合格品与2件次品的100件产品中任意抽出4件：
    (1)抽出的4件产品恰有1件是次品的抽法有多少种
    (2)抽出的4件产品至少有1件是次品的抽法有多少种
    (3)抽出的4件产品都是合格品的抽法有多少种


    答案：
    解析：

  • 第18题：

    桌子上有10个杯子，其中有2个次品，现从中随机抽取3件，则其中至少有一个次品的概率为（ ）。
    A. 0. 47 B.0.53 C. 0.67 D. 0.93


    答案：B
    解析：

  • 第19题：

    已知甲、乙两箱中装有同种产品，其中甲箱中装有3件合格品和3件次品，乙箱中仅装有3件合格品.从甲箱中任取3件产品放入乙箱后，求：
    　　(1)乙箱中次品件数X的数学期望；
    　　(2)从乙箱中任取一件产品是次品的概率.


    答案：
    解析：

  • 第20题：

    甲、乙、丙三车间加工同一产品，加工量分别占总量的25％、35％、40％，次品率分别为0．03、0．02、0．01。现从所有产品中取一件，试求：(1)该产品是次品的概率；(2)若检查结果显示该产品是次品。则该产品是乙车间生产的概率是多少


    答案：
    解析：

  • 第21题：

    一批产品共有10个正品和2个次品，任意抽取两次，每次抽一个，抽出后不再放回，则第二次抽出的是次品的概率为（）.


    正确答案:2/5

  • 第22题：

    如果100件产品中，有10件次品，不放回地从中接连抽取两次，每次抽取一件，则第二次取到次品的概率是1/10


    正确答案:正确

  • 第23题：

    问答题
    21.某工厂中，三台机器分别生产某种产品总数的25％，35％，40％，它们生产的产品中分别有5％，4％，2％的次品，将这些产品混在一起，现随机地取一产品，问它是次品的概率是多少?又问这一次品是由三台机器中的哪台机器生产的概率最大?

    正确答案：
    解析：

相关内容