一个口袋中装有3个一样的球，3个球上分别写有数字2，3和4。若第一次从袋子中取出一个球，记下球上的数字A，并将球放回袋中。第二次又从袋子中取出一个球，记下球上的数字B。然后算出它们的积。则所有不同取j求情况所得到的积的和是（）。

题目

相似考题

1.一个口袋中装有3个一样的球，3个球上分别写有数字2，3和4。若第一次从袋子中取出一个球，记下球上的数字A，并将球放回袋中。第二次又从袋子中取出一个球，记下球上的数字B，然后算出它们的积。则所有不同取球情况所得到的积的和是。A．52B．56C．75D．81

2.袋子中有70个红球，30个黑球，从袋中任意摸出一个球，观察颜色后放回袋中，再摸第二个球，观察颜色后也放回袋中。（1）求两次摸球均为红球的概率；（3分）（2）求两次摸球颜色不同的概率。（4分）

3.袋子中有70个红球，30个黑球，从袋中任意摸出一个球，观察颜色后放回袋中，再摸第二个球，观察颜色后也放回袋中。 (1)求两次摸球均为红球的概率；(3分) (2)求两次摸球颜色不同的概率。(4分)

4.袋子中有若干黑球和白球。若取出一个黑球，则袋中黑球占总球数的；若取出两个白球，则袋中白球占。从原来袋中抽出3个球，其中有且仅有1个黑球的概率：A.低于20% B.在20%—40%之间 C.在40%—60%之间 D.高于60%

更多“ 一个口袋中装有3个一样的球，3个球上分别写有数字2，3和4。若第一次从袋子中取出一个球，记下球上的数字A，并将球放回袋中。第二次又从袋子中取出一个球，记下球上的数字B。然后算出它们的积。则所有不同取j求情况所得”相关问题

第1题：

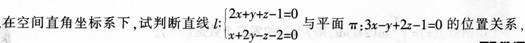
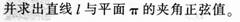袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，且第一次摸出的球，不放回袋中：
(1)求两次摸球均为红球的概率：
(2)若第一次摸到红球，求第二次摸到黑球的概率。

答案：
解析：
平面π的法向量为n=(3，-1，2)；
第2题：

3、一个袋子中装有3个红色球，5个白色球，甲取出了一个红球，不再放回袋子中，乙也从袋子中摸一个球，他取出红球的概率是_____。（保留三位有效数字）

\frac {13}{28}
第3题：

假如某口袋中装有大小相同的黑、白球各1个。从中任取1个，若取出白球，则摸球停止，若取出黑球，则把取出的黑球放回的同时，在加入一个黑球，如此下去，直到取出白球为止。求第5次才取到白球的概率。

（1）用a、b表示两个白球，c、d、e表示三个黑球．现从口袋中随机地摸出一个球，其基本事件有以下五种： {a}，{b}，{c}，{d}，{e}；…（2分）设恰好是白球的事件为A，其中A包括两个基本事件：{a}，{b}．…（4分）故可得A事件的概率P（A）= 2 5 …（6分）（2）若从口袋中一次随机地摸出两个球，其基本事件有以下十种： {a，b}，{a，c}，{a，d}，{a，e}，{b，c}，{b，d}，{b，d}，{c，d}，{c，e}，{d，e}； …（8分）设恰好都是白球的事件为B，它包括的基本事件有一个：{a，b}．…（10分）故可得B事件的概率P（B）= 1 10 …（12分）
第4题：

袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，而且是不放回的摸球：

（1）求两次摸球均为红球的概率。

（2）若第一次摸到红球，求第二次摸到黑球的概率。

答案：
解析：
本题主要考查求解随机事件的概率方法。

（1）利用概率近似等于频率，根据相互独立性，可求解两次摸球都是红球的概率。

（2）由于第一次摸到红球，从剩余的99个球中摸一个黑球，共有30种可能。
第5题：

10、从装有3个红球2个白球的口袋中一个一个地取球，共取了四次，取出X个红球，Y个白球，若每次取出的球立即放回袋中，再取下一个，则X=2,Y=2的概率为
A．0.3456
B．0.1536
C．0.1296
D．0.0256

取出一个红球得5分，取到一个白球得2分，取到一个黄球得1分，从袋中取出5个球，使得总分大于10分且小于15分的取法， 2红3黄C 2 2 ?C 5 2 =10 2红1白2黄C 2 2 ?C 3 1 ?C 5 2 =30 1红3白1黄C 2 1 ?C 3 3 ?C 5 1 =10 1红2白2黄C 2 1 ?C 3 2 ?C 5 2 =60 总数为10+30+10+60=110，故选C．

题目

相似考题

相关内容