一辆车从甲地开往乙地，如果车速提高20%，可以比原定时间提前一小时到达；如果以原速行驶120千米后，再将速度提高25%，则可提前40分钟到达。问：甲、乙两地相距多少千米?（ ）

题目

一辆车从甲地开往乙地，如果车速提高20%，可以比原定时间提前一小时到达；如果以原速行驶120千米后，再将速度提高25%，则可提前40分钟到达。问：甲、乙两地相距多少千米?（ ）

相似考题

1.五、应用题（本大题共3小题，共25分）第 18 题 某团体从甲地到乙地，甲、乙两地相距100千米，团体中一部分人乘车先行，余下的人步行，先坐车的人到途中某处下车步行，汽车返回接先步行的那部分人，已知步行速度为8千米／4,时，汽车速度为40千米／小时。问使团体全部成员同时到达乙地需要多少时间?(8分)

2.甲、乙两地相距600千米，一辆汽车原计划用12小时从甲地开往乙地，行驶到路程一半，因车辆故障停留了1小时，如果要按原定时间到达乙地，那么汽车时速需加快多少?（ ）A．30%B．25%C．20%D．15%

3.一辆车从甲地开往乙地，如果车速提高20％，可以比原定时间提前一小时到达；如果以原速行驶l20千米后，再将速度提高25％，则可提前40分钟到达。问：甲、乙两地相距多少千米?( )A.225B． 270C． 450D． 720

4.：某团体从甲地到乙地，甲、乙两地相距l00千米，团体中一部分人乘车先行，余下的人步行，先坐车的人到途中某处下车步行，汽车返回接先步行的那部分人，已知步行速度为8千米/小时，汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间？（ ）A．5.5小时B．5小时C．4.5小时D．4小时

更多“ 一辆车从甲地开往乙地，如果车速提高20%，可以比原定时间提前一小时到达；如果以原速行驶120千米后，再将速度提高25%，则可提前40分钟到达。问：甲、乙两地相距多少千米?（ ） ”相关问题

  • 第1题：

    甲、乙两车分别从A、B两地出发，相向而行，出发时，甲、乙的速度比是5：4，相遇后，甲的速度减少20%，乙的速度增加20%，这样，当甲到达B时，乙离A地还有10千米。那么A、B两地相距多少千米？

    A．450

    B．500

    C．540

    D．600


    正确答案：A

  • 第2题：

    甲、乙两车从A、B两地同时出发，相向而行。如果甲车提前一段时间出发，那么两车将提前30分相遇。已知甲车速度是60千米/时，乙车速度是40千米/时。那么，甲车提前了多少分出发( )。

    A.30 B.40 C.50 D.60


    正确答案：C

  • 第3题：

    甲、乙两地相距600公里，一辆汽车原计划用12小时从甲地开往乙地，行驶到路程一半，因车辆故障停留了1小时，如果要按原定时间到达乙地，那么汽车时速需加快多少?（ ）

    A．30%

    B．25%

    C．20%

    D．15%


    正确答案：C
    汽车原时速为600÷12=50(公里/小时)，设汽车后半段路程的行驶速度每小时加快x公里，根据速度×时间=路程的公式，可得：(50+x) ×(12÷2-1)=600÷2，解得x=10。比原来的时速加快了10÷50×100%=20%，本题正确答案为C。

  • 第4题：

    从甲地到乙地的公路，只有上坡路和下坡路，没有平路，一辆汽车上坡时每小时行驶20千米，下坡时每小时行驶35千米。车从甲地开往乙地需9小时，从乙地到甲地需小时，问：甲、乙两地间的公路有多少千米？（ ）

    A. 300

    B. 250

    C. 210

    D. 200

  • 第5题：

    一辆车从甲地开往乙地，如果提速20%，可比原定时间提前1小时到达，如果以原速行驶120千米后，再将速度提高25%，则可提前40分钟到达。问甲乙两地相距多少千米：
    A240
    B250
    C270
    D300


    答案：C
    解析：

  • 第6题：

    王经理从甲地到乙地出差，计划乘坐时速为80千米的汽车出发，可以在预定时间内到达。实际临时决定乘坐时速为140千米的火车出发，结果提前3小时到达。问甲、乙两地相距多少千米？

    A.560
    B.580
    C.540
    D.520

    答案：A
    解析：
    设预订到达时间为t小时，则可以列方程为80t=140(t－3)，解得t=7。则甲乙两地之间的路程为7x80=560千米。

  • 第7题：

    小王从单位开车去省城，如果他把车速提高20％，可以比原定时间提前15分钟到达；如果按原速度行驶30千米后再将车速提高到25％，也比原定时间提前15分钟到达。问小王单位距离省城多少千米？（ ）

    A.60
    B.120
    C.180
    D.240

    答案：C
    解析：
    第一步，本题考查行程问题，用比例法解题。

  • 第8题：

    一辆车从甲地开往乙地，如果提速20％，可以比原定时间提前一小时到达。如果以原速走120千米后，再将速度提高25％，则可提前40分钟到。那么甲、乙两地相距多少千米？

    A. 240
    B. 270
    C. 250
    D. 300

    答案：B
    解析：
    提高20%，速度比5：6，时间比6：5，刚好差1小时，所以原来6小时，提速后5小时。提高25%，速度比5：4，时间比4：5，差2/3，所以原来是5*2/3=10/3小时，行了120千米。时间是6-10/3=8/3，120/8/3=45，45*6=270。故答案为B。

  • 第9题：

    一辆车从甲地开往乙地，如果提速20%，可以比原定时间提前1小时到达，如果以原速行驶120千米后，再将速度提高25%，则可提前40分钟到达。 问甲乙两地相距多少千米：
    A240
    B250
    C270
    D300


    答案：C
    解析：

  • 第10题：

    小张和小马分别从甲、乙两地同时出发，相向而行，出发时他们的速度之比是5∶3，第一次相遇后，小张的速度提高了20％，小马的速度提高了50％，这样，当小张到达乙地时，小马离甲地还有11千米，那么甲、乙两地的距离是多少？

    A.20千米
    B.24千米
    C.32千米
    D.40千米

    答案：C
    解析：
    设甲、乙两地相距8ｘ千米，由于小张和小马的速度之比为5∶3，所以当他们初次相遇时小张走了5ｘ千米，小马走了3ｘ千米。之后二人速度改变，他们的速度之比变为［5×（1＋20％）］∶［3×（1＋50％）］＝4∶3，此后小张继续走3ｘ千米到达乙地，则相同时间内小马走的距离是(3/4)×3x=(9/4)x千米，此时小马距离甲地还有11千米，即5x-(9/4)x=11，解得ｘ＝4，则甲、乙两地相距4×8＝32千米。故本题选C。

  • 第11题：

    一项工程进行m天之后，速度如果提高20%，则可以提前n天完工，问速度如果提高50%，则可以提前多少天完工？

    A.2n
    B.2.5n
    C.2n+m
    D.2.5n+m

    答案：A
    解析：
    正反比例。剩余的工作量一定，工作效率和工作时间成反比关系。如果提高20%，原速和现速之比为5:6，所需时间之比为6:5，少用一份时间少用n天，一份代表n天，说明剩余工作按原来效率来干需要6n天。速度如果提高50%，原速和现速之比为2:3，所需时间之比为3:2，原来需要三份时间，需要6n天，一份时间为2n，少用一份时间，少用2n天。因此答案选A。

  • 第12题：

    某团体从甲地到乙地，甲、乙两地相距100千米，团体中一部人乘车先行，余下的人步行，先坐车的到途中某处下车步行，汽车返回接先步行的那部分人，已知步行速度为8千米/小时，汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间。

    A、5.5小时 B、5小时 C、4.5小时 D、4小时


    正确答案：B

  • 第13题：

    某团体从甲地到乙地，甲、乙两地相距100千米，团体中一部分人乘车先行，余下的人步行，先坐车的人到途中某处下车步行，汽车返回接先步行的那部分人，全部人员同时到达。已知步行速度为8千米/小时，汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?( )

    A．5.5小时

    B．5小时

    C．4.5小时

    D．4小时


    正确答案：B
    B  [解析]因为两队是同时出发又同时到达的，所以两队步行的距离相等，乘车的距离也相等。设第一队乘车的距离是x，则步行的距离是100-x，那么第二队步行的距离也是100-x，汽车从第一队人下车到回来与第二队相遇的距离是：100-2(100-x)=2x-100，因为汽车从出发到与第二队相遇的时间与第二队步行的时间相同。所以列方程：(z+(2x-100)]÷40=(100-x)÷8，解得x=75，那么一共所用的时间是：75÷40+(100-75)÷8=5(小时)，故选B。

  • 第14题：

    一辆汽车从甲地开往乙地，每小时行40千米，开出5小时后，一列火车以每小时90千米的速度也从甲地开往乙地。在甲乙两地的中点处火车追上汽车，甲乙两地相距多少千米？（ ）

    A．724

    B．720

    C．698

    D．722


    正确答案：B

    解这道题的关键是火车行至追及处所行的路程是多少千米。要想求出火车所行的路程，就要先求追及的时间。要想求出追及的时间，就要先求出路程差和速度差：90×[40×5÷(90-40)]×2＝720(千米)。

  • 第15题：

    小李驾车从甲地去乙地。如果比原车速提髙25%，则比原定时间提前30分钟到达。原车速行驶120千米后，再将车速提高25%，可提前15分钟到达，则原车速是（ ）。

    A. 84千米/小时
    B. 108千米/小时
    C. 96千米/小时
    D. 110千米/小时

    答案：C
    解析：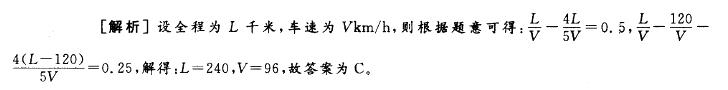

  • 第16题：

    一架战斗机从甲机场匀速开往乙机场，如果速度提高25%，可比原定时间提前12分钟到达，如果以原定速度飞行600千米后，再将速度提高三分之一，可以提前5分钟到达。那么甲乙两机场的距离是多少千米？

    A.750
    B.800
    C.900
    D.1000

    答案：C
    解析：
    第一步，本题考查行程问题，属于基本行程类，用比例法解题。
    第二步，设原速度为v千米/分钟。根据路程相等时，速度之比等于时间的反比，由v∶（1＋25%）v＝4∶5，则时间之比为5∶4，故“提前12分钟到达”，时间差1份，1份为12分钟，原速度飞行的时间为5份，则按原速度飞行需要60分钟。
    第三步，如果以原定速度飞行600千米后，再将速度提高三分之一，可以提前5分钟到达。路程为60v－600，速度比为v∶（1+

    ）v＝3∶4，可得时间之比为4∶3，则时间差为1份，即5分钟，则4份时间为20分钟，则40分钟可飞行600千米，60分钟可飞行900千米，即全程。

  • 第17题：

    王经理从甲地到乙地出差，计划乘坐时速为80千米的汽车出发，可以在预定时间内到 达。实际临时决定乘坐时速为140千米的火车出发,结果提前3小时到达。问甲、乙两地相距多 少千米？

    A.560
    B.580
    C.540
    D.520

    答案：A
    解析：
    设预订到达时间为t小时，则可以列方程为80t=140(t-3)，解得t=7。则甲乙两地之间的 路程为7x80=560千米。

  • 第18题：

    小李驾车从甲地去乙地，如果比原车速提高25%,则比A原定时间提前30分钟到达；如按原车速行驶120千米后，再将车速提高25%，可提前15分钟到达，则原车速是：

    A.84千米/小时
    B.108千米/小时
    C.96千米/小时
    D.110千米/小时

    答案：C
    解析：
    全程提速提前30分钟到达，部分路程提速提前15分钟到达，因此部分提速的路程相当于全程的一半，全程为原速行驶路程的2倍，即120x2=240千米。原速度：加速后速度=1：(1+25%)，用时比为其反比5：4。两者相差30分钟，即原速走完全程要5x30=150分钟=2.5小时，原来的车速是240÷2.5=96千米/小时。

  • 第19题：

    某部队从驻地乘车赶往训练基地，如果车速为54公里/小时，正好准点到达；如果将车速提高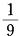，就可比预定的时间提前20分钟赶到；如果将车速提高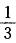，可比预定的时间提前多少分钟赶到？（）

    A. 30
    B. 40
    C. 50
    D. 60

    答案：C
    解析：
    设准点到达的时间为t,则有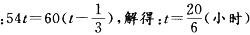

    所以总路程为如果将车速提高，则车速为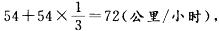需要时间为180÷72=2.5（小时），比预定的时间提前

  • 第20题：

    如下图，A、C两地相距2千米，C、B两地相距5千米。甲、乙两人同时从C地出发，甲向B地走，到达B地后立即返回；乙向A地走，到达A地后立即返回。如果甲速度是乙速度的1.5倍，那么在乙到达D地时，还未能与甲相遇，他们还相距0.5千米，这时甲距C地多少千米？（ ）

    A. 1.4 B. 1.9 C. 2.3 D. 3.3


    答案：B
    解析：
    由甲速是乙速的1.5倍，可知甲所走路程是乙所走路程的1.5倍。设C、D距离为x 千米，则乙走的路程是(4+x)千米，甲所走路程为(4+x)X1. 5千米，根据题意有(4+x)X1.5 = 5X2-x-0. 5，解得：x=1.4，此时甲距C地1. 4 + 0. 5 = 1. 9(千米)，本题正确答案为B。

  • 第21题：

    甲、乙两货车同时从相距300千米的A、B两地相对开出，甲车以每小时60千米的速度开往B地，乙车以每小时40千米的速度开往A地，甲车到达B地停留2小时后以原速返回，乙车到达A地停留半小时后以原速返回。那么，返回时两车相遇地点与A地相距____千米。

    A. 60
    B. 84
    C. 96
    D. 110

    答案：C
    解析：
    甲车从A地到达B地行驶及等待的时间为300÷60+2=7（小时）；乙车从A地到达B地行驶及等待的时间为300÷40+0.5=8（小时）。即甲车从B地先行8-7=1（小时）。因此，甲车从B地先行1小时后（走60千米），乙车才从A地出发．所以，两车返回时的相遇时间是（300-60）÷（60+40）=2.4（小时）。故两车返回时相遇地点与A城相距40×2.4=96（千米）。所以选C。

  • 第22题：

    单选题
    甲、乙两地相距280千米，小张开汽车从甲地出发，开始时以72千米／时的速度行驶，但途中因汽车故障停车修理半小时，为按时到达乙地，他在余下路程中速度必须增加18千米／时，则他修车的地方距甲地：
    A

    80千米

    B

    100千米

    C

    120千米

    D

    180千米


    正确答案： A
    解析： 暂无解析

相关内容