浙江省富阳市场口中学0910学年高二下学期5月质检理数缺答案
A、若AB=AC,则B=C
B、(A-C)^2=A^2-2AC+C^2
C、ABC=BCA
D、|ABC|=|A||B||C|
设A与B是任意两事件,则A-B=( )。
A.A-AB
B.B-AB
C.AB
D.A(口-B)
E.AB-A
设X=ab,Y=cd分别为2位二进制正整数,X>Y的逻辑表示式是( )。
A.ac + abd + bcd
B.ac + adb + bcd
C.ad + abc + bed
D.ac + bcd + abd
设X=ab,Y=cd分别为2位二进制正整数,X>Y的逻辑表示式是( )。
A.ac+aM+bcd
B.ac+adb+bcd
C.ad+abc+bcd
D.ac+bcd+abd
设关系模式R(A,B,C,D,E),F是R上成立的FD集,F={AB→C,BC→A,AC→B,D→ E },R的候选键为(1)。
A.ABC、ACD、ACE
B.ABD、BCD、ACD
C.ABC、BCD、ACD
D.ABD、ACD、ACE
解析:模式R有三个候选键:ABD、BCD、ACD三个。推导过程如下:①从AB→C和D→E,可推出ABD→ABCDE。②从BC→A和D→E,可推出BCD→ABCDE。③从AC→B和D→E,可推出ACD→ABCDE。
场口中学2022 年 5 月教学质量检测高二数学试题卷(理科)A.B.C.D.图 12222在平面几何里,有勾股定理: “设 ABC的两边 AB, AC互相垂直,则 AB+AC=BC”拓展到空间,类比平面几何的勾股定理, “设三棱锥 A BCD 的三个侧面 ABC、ACD、ADB 两两相互垂直,则可得”( )22222+AC+ AD =BC+ CD + BDB.2SABC2S222222ACD2SADBS BCD一. 选择题(本大题共10 小题,每小题3 分,共 30 分)1在复平面内,与复数zA. 第一象限B. 第二象限1C.i 的共轭复数对应的点位于()第三象限D. 第四象限2. 函数 yx1B.ln2,2xA. 1,的定义域是C.()D.3. 函数f ( x)ex1的零点所在的区间是x()A (0, 1 )B.2( 1 ,1)2C (1,3 )2D.( 3 , 2)24已知是实数,则“”是“a 3b3”的()A充分而不必要条件C 充分必要条件y 2B.必要而不充分条件D.既不充分也不必要条件4 与圆 C : x 25若圆 O : x 2y 24 x4 y40 ,关于直线对称,则直线方程为()A xy0B xy0C xy20D xy206在二项式(x21 )5 的展开式中,含的项的系数是x()ABCD7设函数 f(x)在定义域内可导, y=f(x)yy的图象如图y1 所示,则导函数y=fy(x) 可能为 ()yOxOxOxOxOxC. S 2ABCS 2 ACDS 2 ADBS 2 BCDDAB AC AD=BC CD BDxy20 xy设实数满足2 y50,则 u的最小值是()xA 13204C.3D 3已知为上的可导函数,且f (x)f (x)和0对于 xR恒成立 , 则有()f( 2)e2f(0),f (2010)e2010f (0)f( 2)e2f(0),f (2010)e 2010f (0)f(2)e 2f (0),f ( 2010)e 2010f (0)f( 2)e2f(0),f (2010)e2010f (0)二、填空题: (本题 7 小题,每小题4 分,共 28 分)命题“ R, x3x 2110n 的否定是.某校举行2022 年元旦汇演, 七位评委为某班的小品打出的分数(百分制)如下茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的中位数和方差分别为,如右图,该程序运行后输出的结果为.若某多面体的三视图(单位:)如图所示,则此多面体的体积是7984 46 4793开始a1,b1否3?33正视图3侧视图是2 b输出 b3俯视图(第 14 题)aa1结束(第 13 题)已知:B( n,p) ,若 E3D,则=.现有 5 根竹竿,它们的长度(单位:m)分别为, ,若从中一次随机抽取2 根竹竿, 则它们的长度恰好相差0.3m 的概率为.x2y2已知双曲线221,( aab0, b0) 的左,右焦点分别为F1 , F2 ,点 P 在双曲线的右支上,且| PF1|4 | PF2|,则此双曲线的离心率e 的最大值为.三、解答题:本大题共4 小题,满分42 分18(本题 8 分)在 5 件产品中有2 件次品,连续抽3 次,每次抽1 件,求:不放回抽样时,抽到次品数的分布列;放回抽样时,抽到次品数的分布列.19. (本题 10 分)如图,在三棱柱为侧棱的中点 .ABCA1B1C1 中,每个侧面均为正方形,为底边的中点,A 1()求证:平面C1A1EB ;B 1()求证:AB1平面 A1EB ;E()求直线与平面AA1C1C 所成角的正弦值.ACDBx2y2620(本题10 分)已知椭圆221(ab ab0) 的离心率为,短轴的一个端点到右3焦点的距离为 , 直线 l : ykxm 交椭圆于不同的两点, ()求椭圆的方程;()若 mk ,且OA OB0 ,求的值(点为坐标原点);21(本题 14 分)已知函数f ( x)x2xa ln x()当时,f (x)x2 恒成立,求的取值范围;()讨论在定义域上的单调性;
设X=ab,Y=cd分别为2位二进制正整数,x>Y的逻辑表示式是( )。
A.ac+abd+bcd
B.ac+adb+bcd
C.ad+abc+bcd
D.ac+bcd+abd
B.P(A-B-C)=P(A)-P(AB)-P(AC)+P(ABC)
C.P(A-B-C)=P(A)-P(AB)-P(BC)+P(ABC)
D.P(A-B-C)=P(A)-P(AC)-P(BC)+P(ABC)

B.P(A-B-C)=P(A)-P(AB)-P(AC)+P(ABC)
C.P(A-B-C)=P(A)-P(AB)-P(BC)+P(ABC)
D.P(A-B-C)=P(A)-P(AC)-P(BC)+P(ABC)

B.P(A-B-C)=P(A)-P(AB)-P(AC)+P(ABC)
C.P(A-B-C)=P(A)-P(AB)-P(BC)+P(ABC)
D.P(A-B-C)=P(A)-P(AC)-P(BC)+P(ABC)
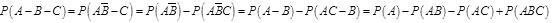
B.P(A-B-C)=P(A)-P(AB)-P(AC)+P(ABC)
C.P(A-B-C)=P(A)-P(AB)-P(BC)+P(ABC)
D.P(A-B-C)=P(A)-P(AC)-P(BC)+P(ABC)

更多 “浙江省富阳市场口中学0910学年高二下学期5月质检理数缺答案” 相关考题
相关内容
最新试卷
热门试卷
- 扬州大学859动物生理学与动物生物化学历年考研真题汇编合集-
- 武汉大学法学院《627综合知识(含法理、宪法、行政法、民法、国际法)》历年考研真题汇编(含部分答案)合集-
- 青岛理工大学商学院经济学历年考研真题汇编合集-
- 武汉大学法学院综合知识(含628综合知识、629综合知识等)历年考研真题汇编(含部分答案)合集-
- 西南大学外国语学院《448汉语写作与百科知识》[专业硕士]历年考研真题及详解合集-
- 国际关系学院英语语言文学712英语语言文学《专业基础》历年考研真题汇编(含部分答案)合集-
- 武汉大学《655分析化学和物理化学》历年考研真题汇编(含部分答案)合集-
- 青岛大学商学院859管理学(2)历年考研真题汇编合集-
- 苏州大学外国语学院244法语历年考研真题汇编合集-
- 西南大学《834生物化学》历年考研真题汇编合集-
